Amid all our concern for face degrees equal to and greater than
Amid all our concern for face degrees equal to and greater than
![]() , the reader may have noticed the conspicuous absence
of
, the reader may have noticed the conspicuous absence
of ![]() -faces, corresponding to
-faces, corresponding to
![]() leaf angles,
which would complete the range of possible values.
leaf angles,
which would complete the range of possible values.
Two equivalent types of ![]() -faces can be built both of which involve
placing the hinges in line with one another. The first method superimposes
the hinges, as in fig. 11.1a. The second puts them side by side
(fig. 11.1b). The only advantage of one over the other is that the second
method allows us to reverse the position of the
-faces can be built both of which involve
placing the hinges in line with one another. The first method superimposes
the hinges, as in fig. 11.1a. The second puts them side by side
(fig. 11.1b). The only advantage of one over the other is that the second
method allows us to reverse the position of the ![]() pat (or leaf)
in respect to the two leaves it joins (See fig. 11.1b. Forcing is still
necessary).
pat (or leaf)
in respect to the two leaves it joins (See fig. 11.1b. Forcing is still
necessary).

Clearly, a ![]() -face will be made up of a set of flaps, joined along a line
at the center of the flexagon. Since this is like the folded-together
position in non
-face will be made up of a set of flaps, joined along a line
at the center of the flexagon. Since this is like the folded-together
position in non ![]() -face flexagons, we are tempted to open it
out. Nothing prevents doing this, since the flaps of the
-face flexagons, we are tempted to open it
out. Nothing prevents doing this, since the flaps of the ![]() -face cannot
lock sides out of sight. Thus most 0
-face cannot
lock sides out of sight. Thus most 0![]() -faces are not only
-faces are not only
![]() -faces, but exhibit a third side as well, which may have
any face degree; if
-faces, but exhibit a third side as well, which may have
any face degree; if ![]() , we can open out again, until one face degree
, we can open out again, until one face degree
![]() is obtained. In a sense, then,
is obtained. In a sense, then, ![]() -faces
can be completely ignored in working the flexagon. On the other hand,
since they are incapable of locking shut,
-faces
can be completely ignored in working the flexagon. On the other hand,
since they are incapable of locking shut, ![]() -faces tend
to lessen the flexagon's stability greatly. For this reason most of the
research done heretofore seems to have avoided them. However, Dr. F. G.
Mannsell and Miss Joan Crampin 11.1, present
a notable exception; the irony of the situation being that their interest
was apparently due to a misunderstanding of the significance of the
regular triflexagon of order 6, which was presented in an article by Miss
Margaret Joseph11.1. The order 6 flexagon they
discuss will, however, serve ideally for introducing
-faces tend
to lessen the flexagon's stability greatly. For this reason most of the
research done heretofore seems to have avoided them. However, Dr. F. G.
Mannsell and Miss Joan Crampin 11.1, present
a notable exception; the irony of the situation being that their interest
was apparently due to a misunderstanding of the significance of the
regular triflexagon of order 6, which was presented in an article by Miss
Margaret Joseph11.1. The order 6 flexagon they
discuss will, however, serve ideally for introducing ![]() -faced
flexagons. It is built from a straight strip of 18 equilateral
triangles, folded up in the constant order 1 2 3 4 5 6. Thus its map is
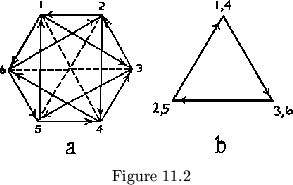
that shown in figure 11.2a. It is, of course, a hexa-flexagon. We were
told that these could not be made of triangles without hinges overlapping:
this is precisely what happens in this flexagon. A simple calculation
shows which sides will appear together as
-faced
flexagons. It is built from a straight strip of 18 equilateral
triangles, folded up in the constant order 1 2 3 4 5 6. Thus its map is
that shown in figure 11.2a. It is, of course, a hexa-flexagon. We were
told that these could not be made of triangles without hinges overlapping:
this is precisely what happens in this flexagon. A simple calculation
shows which sides will appear together as ![]() -faces: those connected by
dotted lines in the figure. When we have built this flexagon, we are
surprised to see that, except for numbering, it is identical with the
triflexagon of order 3, made with 6 units. This, too, is explained by
the map. Suppose we erase the numbers off the leaves. Then sides making
up
-faces: those connected by
dotted lines in the figure. When we have built this flexagon, we are
surprised to see that, except for numbering, it is identical with the
triflexagon of order 3, made with 6 units. This, too, is explained by
the map. Suppose we erase the numbers off the leaves. Then sides making
up ![]() faces will be indistinguishable, and, if they are drawn as one point,
we get the map in figure 11.2b, from the map in fig. 11.2a. This second
map is much more easily read than the first, but is difficult to use in
making the flexagon. It is therefore recommended that each form be used
for the better-suited purpose, making or operating, only.
faces will be indistinguishable, and, if they are drawn as one point,
we get the map in figure 11.2b, from the map in fig. 11.2a. This second
map is much more easily read than the first, but is difficult to use in
making the flexagon. It is therefore recommended that each form be used
for the better-suited purpose, making or operating, only.
Miss Crampin points out that any combination of the sides at one vertex
of a map such as that in fig. 11.2b and the sides at an adjoining vertex
can occur. Not only is this true, but the sides at one vertex can be mixed,
so that a number appear at one time. This is a further reason to consider
0![]() face sides as identical. An interesting figure that demonstrates
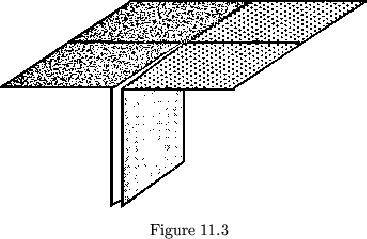
how the sides at each vertex can mix is shown in fig. 11.3. It should be
marked according to the number sequence
face sides as identical. An interesting figure that demonstrates
how the sides at each vertex can mix is shown in fig. 11.3. It should be
marked according to the number sequence
![]() . The flap
on this object travels around the object's center. The 0
. The flap
on this object travels around the object's center. The 0![]() faced
flexagon may be made to do the same thing, with its three flaps.
faced
flexagon may be made to do the same thing, with its three flaps.
Aside from the points already mentioned, 0![]() faced flexagons have
little to distinguish themselves from other flexagons. Both types (either
may be used in most cases) are made using only slight alterations of the
usual construction method. The map requires no changes at all. To see
how any 0
faced flexagons have
little to distinguish themselves from other flexagons. Both types (either
may be used in most cases) are made using only slight alterations of the
usual construction method. The map requires no changes at all. To see
how any 0![]() faced flexagon can actually be put together we
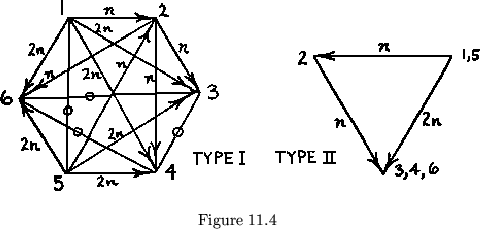
consider the flexagon in figure 11.4. The first thing that strikes one
is the comparative simplicity of the second map. The first map, however,
shows each possible pairing of the sides into faces separately. Since
this is true, we also notice in the first map that paths leading to
opposite ends of 0
faced flexagon can actually be put together we
consider the flexagon in figure 11.4. The first thing that strikes one
is the comparative simplicity of the second map. The first map, however,
shows each possible pairing of the sides into faces separately. Since
this is true, we also notice in the first map that paths leading to
opposite ends of 0![]() face from the same side are of equal degree. This
is characteristic of 0
face from the same side are of equal degree. This
is characteristic of 0![]() faced flexagons, and,
if no 0
faced flexagons, and,
if no 0![]() faces are present in the
faces are present in the ![]() -cut cycle,
so that their signs are readily seen, the presence of
-cut cycle,
so that their signs are readily seen, the presence of ![]() and
and ![]() signs
in the sign sequence, for one cycle, may help indicate their presence.
Another sure indication of the presence of 0
signs
in the sign sequence, for one cycle, may help indicate their presence.
Another sure indication of the presence of 0![]() faces in a flexagon is
that its class may be less than its cycle. This forces some of the hinges
to overlap, so that 0
faces in a flexagon is
that its class may be less than its cycle. This forces some of the hinges
to overlap, so that 0![]() faces result. The
faces result. The ![]() used in the maps
given indicates that any angle will be adequate in place of
used in the maps
given indicates that any angle will be adequate in place of ![]() . Let us
choose 120
. Let us
choose 120![]() , so that the map becomes like fig. 10.12.
, so that the map becomes like fig. 10.12.
By the method described in the last section (sect X, part D), we
find, for the sign sequence,
![]() , where
, where
![]() .
The number sequence is of course
.
The number sequence is of course
![]() ,
with three units. The only irregularity comes in the handling of the
0
,
with three units. The only irregularity comes in the handling of the
0![]() leaf. The leaf following this
leaf can be placed either above it or below it; unless we either use the
double hinge position type of zero flex or superimpose the new hinge in
the correct place, the flexagon will not fit together. To determine the
correct position; count either up or down away from the number on top of the
0
leaf. The leaf following this
leaf can be placed either above it or below it; unless we either use the
double hinge position type of zero flex or superimpose the new hinge in
the correct place, the flexagon will not fit together. To determine the
correct position; count either up or down away from the number on top of the
0![]() leaf, just so long as the number on the bottom of the leaf is not
encountered. When a number occurring in either the last leaf before the
0
leaf, just so long as the number on the bottom of the leaf is not
encountered. When a number occurring in either the last leaf before the
0![]() leaf or the next leaf is encountered, stop. If the number encountered
was on the leaf before the 0
leaf or the next leaf is encountered, stop. If the number encountered
was on the leaf before the 0![]() leaf, the new leaf is placed underneath. If
the number was on the new leaf, put the new leaf above. The proof of this
little theorem is not difficult, but it is awkward, so that it is omitted
here.
leaf, the new leaf is placed underneath. If
the number was on the new leaf, put the new leaf above. The proof of this
little theorem is not difficult, but it is awkward, so that it is omitted
here.
When it has been placed correctly, the new leaf must be folded over (or
under) the leaf preceding the 0![]() leaf, before other leaves are added
on. This puts the right surface on the top side of the leaf and orients
it correctly for use with the sign sequence. The remainder of the assembly
is routine. When we are finished, the face (1-5, 3-4-6) should look like
fig. 11.5.
leaf, before other leaves are added
on. This puts the right surface on the top side of the leaf and orients
it correctly for use with the sign sequence. The remainder of the assembly
is routine. When we are finished, the face (1-5, 3-4-6) should look like
fig. 11.5.

The main consequence of the inclusion of 0![]() faced flexagons in our
discussion is the enormous increase in the number of flexagons we can build.
For example, there are now 13 possible 4-flexagons or order 4, made from
squares. All of these have been made; few prove interesting to any great
extent, since most of the type II maps (See fig. 11.4b) are trivial. When
we get around to building 0
faced flexagons in our
discussion is the enormous increase in the number of flexagons we can build.
For example, there are now 13 possible 4-flexagons or order 4, made from
squares. All of these have been made; few prove interesting to any great
extent, since most of the type II maps (See fig. 11.4b) are trivial. When
we get around to building 0![]() faced flexagons of more than one cycle,
though, a new difficulty arises:
flexagons in which any two cycles have a 0
faced flexagons of more than one cycle,
though, a new difficulty arises:
flexagons in which any two cycles have a 0![]() face in
common require two hinge positions at the 0
face in
common require two hinge positions at the 0![]() face. Even when these
are given, as when we use the 2-hinge position type of 0
face. Even when these
are given, as when we use the 2-hinge position type of 0![]() face, the
change of cycle cannot occur. To see why all of this is so, and to
find a remedy for the situation, we must consider the past structure
of an intercycle face. There are two pats, one for each cycle. Each
of these is made up of a pile of subpats (and/or single leaves) arranged
in the pat structure
face, the
change of cycle cannot occur. To see why all of this is so, and to
find a remedy for the situation, we must consider the past structure
of an intercycle face. There are two pats, one for each cycle. Each
of these is made up of a pile of subpats (and/or single leaves) arranged
in the pat structure
![]() , where each letter represents
a subpat, and
, where each letter represents
a subpat, and ![]() is connected to
is connected to ![]() ;
; ![]() to
to ![]() , etc. When these are
joined, they form the constant order
, etc. When these are
joined, they form the constant order
![]() ,
where
,
where ![]() is connected to
is connected to ![]() and
and ![]() to
to ![]() . However,
if we try to use only one inter-pat hinging position
during the 0
. However,
if we try to use only one inter-pat hinging position
during the 0![]() face, the hinge
face, the hinge ![]() blocks off
blocks off ![]() from
from ![]() ,
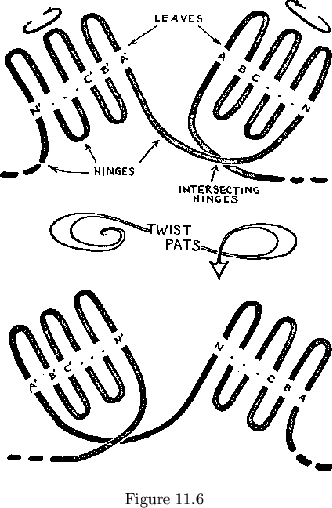
and the two hinges must intersect. (See fig. 11.6, upper half). The figure
shows, even if the hinges are allowed to intersect, by using a double hinge
position type of 0
,
and the two hinges must intersect. (See fig. 11.6, upper half). The figure
shows, even if the hinges are allowed to intersect, by using a double hinge
position type of 0![]() face, one pat (
face, one pat (![]() ) will be locked
shut. This is what prevents further flexing in one of the two cycles.
Yet we can see that if the intersection could be moved, so that
it would occur in front of the subpat
) will be locked
shut. This is what prevents further flexing in one of the two cycles.
Yet we can see that if the intersection could be moved, so that
it would occur in front of the subpat
![]() as shown in fig. 11.6, rather than in front of
as shown in fig. 11.6, rather than in front of
![]() then flexing could occur. The only way to move the
intersection is to rotate both pats about themselves through a half twist,
in opposite directions, so that the crossover is unwound off of the second
pat onto the first. Doing this would add no twists to the strip, but it
does require flexible leaves. Specifically, it requires that the leaves be
creased along the perpendicular drawn to the intersecting hinges at their
midpoints. The ends of the hinges toward the top of the flexagon during the
0
then flexing could occur. The only way to move the
intersection is to rotate both pats about themselves through a half twist,
in opposite directions, so that the crossover is unwound off of the second
pat onto the first. Doing this would add no twists to the strip, but it
does require flexible leaves. Specifically, it requires that the leaves be
creased along the perpendicular drawn to the intersecting hinges at their
midpoints. The ends of the hinges toward the top of the flexagon during the
0![]() face may then be folded down next to the bottom ends, after
which the bottom ends are to be folded up to replace the top ones.
This operation produces the desired result. Fig. 11.7 gives the picture
for the 4-flexagons; other cases are analogous.
face may then be folded down next to the bottom ends, after
which the bottom ends are to be folded up to replace the top ones.
This operation produces the desired result. Fig. 11.7 gives the picture
for the 4-flexagons; other cases are analogous.

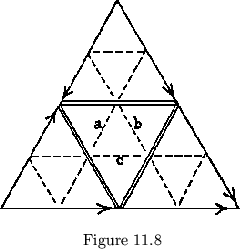
Even this does not clear up all of the difficulty. In the flexagon shown in
fig. 11.8, for example, each of the three hinges ![]() ,
, ![]() , and
, and ![]() will
intersect the others. Suppose that we cut away the bottom
will
intersect the others. Suppose that we cut away the bottom ![]() of hinge a
to make room for hinges
of hinge a
to make room for hinges ![]() and
and ![]() . Then we must cut away the top
. Then we must cut away the top ![]() of
the hinges
of
the hinges ![]() and
and ![]() . However, to make room for hinge
. However, to make room for hinge ![]() , we must the cut
away the bottom
, we must the cut
away the bottom ![]() of hinge
of hinge ![]() , which completely severs it. Hence it is
impossible to have a
, which completely severs it. Hence it is
impossible to have a ![]() cycle of 0
cycle of 0![]() faces, each of which joins to
another cycle.
This difficulty will disrupt the counting of the number of possible
0
faces, each of which joins to
another cycle.
This difficulty will disrupt the counting of the number of possible
0![]() faced flexagons quite a bit.
faced flexagons quite a bit.
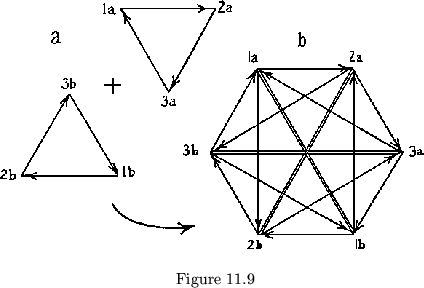
Since each pat of a 0![]() face has a sign sequence sum of zero, the
flexagon could be slit all the way along each 0
face has a sign sequence sum of zero, the
flexagon could be slit all the way along each 0![]() face hinge and put
back together into two smaller flexagons.
The reverse is also possible. Thus the two flexagons in fig. 11.9a, when
each is cut while folded together at
side 1, can combine to form the 0
face hinge and put
back together into two smaller flexagons.
The reverse is also possible. Thus the two flexagons in fig. 11.9a, when
each is cut while folded together at
side 1, can combine to form the 0![]() faced flexagon in fig. 11.9b.
faced flexagon in fig. 11.9b.
0![]() faced flexagons go through other interesting contortions. As
was mentioned, they are quite unstable, so that a number of types of
distortions are possible. The most interesting of these occurs in any
flexagon in which a cutoff 0
faced flexagons go through other interesting contortions. As
was mentioned, they are quite unstable, so that a number of types of
distortions are possible. The most interesting of these occurs in any
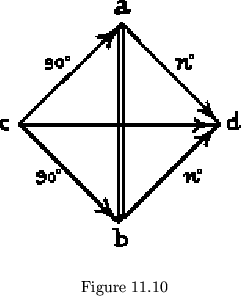
flexagon in which a cutoff 0![]() face and a 90
face and a 90![]() face have a side
in common. Call the 0
face have a side
in common. Call the 0![]() face
face ![]() and the 90
and the 90![]() face
face ![]() .
Then consider another cutoff face,
.
Then consider another cutoff face, ![]() , which crosses
, which crosses ![]() (See fig. 11.10). During this face, the leaves or subpats corresponding
to
(See fig. 11.10). During this face, the leaves or subpats corresponding
to ![]() and
and ![]() will make up one pat, those corresponding to
will make up one pat, those corresponding to ![]() and
and ![]() forming the other. The subpats
forming the other. The subpats ![]() and
and ![]() will both be
either on top or on bottom. The three hinges on
these two subpats will make two right angles, so that they will be able to
open out away from the other two subpats. The simplest example is the map
in fig. 11.10, made from single leaves rather than subpats and with
will both be
either on top or on bottom. The three hinges on
these two subpats will make two right angles, so that they will be able to
open out away from the other two subpats. The simplest example is the map
in fig. 11.10, made from single leaves rather than subpats and with ![]() a
multiple of 90
a
multiple of 90![]() . The position in which the two leaves
. The position in which the two leaves
![]() and
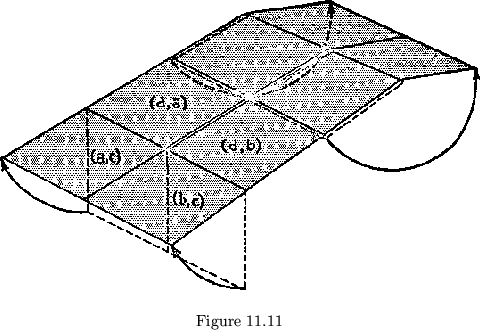
and ![]() open out is shown in fig. 11.11
open out is shown in fig. 11.11
![]() . Since, as was mentioned before,
flexagons with extra units may be considered identical with high-cycle
flexagons of the same class with fewer units, this same distortion can
be produced in some unsuspected places. The proper tetraflexagon of order
4, for example, can be made with 3 units. It may then be considered the
same as the mixed flexagon, half of whose map is that shown in fig. 11.12.
. Since, as was mentioned before,
flexagons with extra units may be considered identical with high-cycle
flexagons of the same class with fewer units, this same distortion can
be produced in some unsuspected places. The proper tetraflexagon of order
4, for example, can be made with 3 units. It may then be considered the
same as the mixed flexagon, half of whose map is that shown in fig. 11.12.
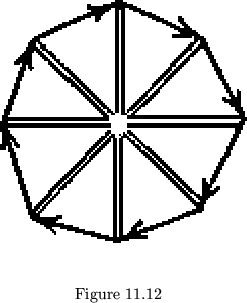
This map satisfies the conditions to the distortion. The reader may recognize that this distortion is the same as flexing half of the order 4 flexagon frontwards, the other half backwards. By adding in still more units, the flexagon may be given more flexes backwards and frontwards at the same time.
0![]() faces may open out at other times, also in a most unexpected manner.
The real reason for this unprecedented phenomenon is to be found in the
flexagon pictured in fig. 11.11. When it is opened out, it is merely a
sheet of paper with a hole in it; it is not twisted at all. The fewer the
twists in a plan, the better the chance of its falling apart, With an
almost arbitrary sequence of face degrees for each cycle, there is a good
chance of getting very few twists. Here is a clue, at least, to instability.
faces may open out at other times, also in a most unexpected manner.
The real reason for this unprecedented phenomenon is to be found in the
flexagon pictured in fig. 11.11. When it is opened out, it is merely a
sheet of paper with a hole in it; it is not twisted at all. The fewer the
twists in a plan, the better the chance of its falling apart, With an
almost arbitrary sequence of face degrees for each cycle, there is a good
chance of getting very few twists. Here is a clue, at least, to instability.
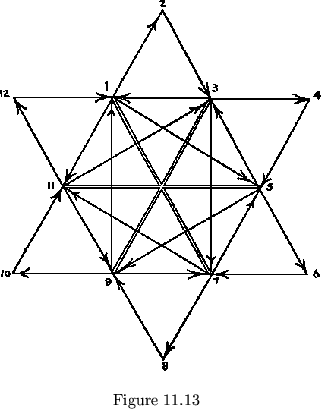
A final ambiguity brought about by 0![]() faces may be seen in the flexagon
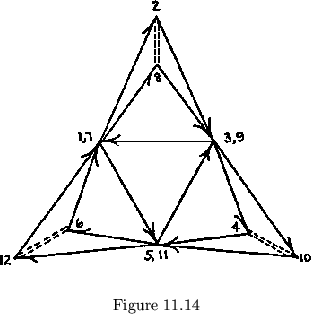
shown in fig. 11.13. When we draw the second type of map for this flexagon,
as in fig. 11.14, we find that the cycles added on to that containing the
0
faces may be seen in the flexagon
shown in fig. 11.13. When we draw the second type of map for this flexagon,
as in fig. 11.14, we find that the cycles added on to that containing the
0![]() faces become indistinguishable. In fact, if the flexagon is treated
as an ordinary regular triflexagon with too many units, the problem sides
do, indeed become a 0
faces become indistinguishable. In fact, if the flexagon is treated
as an ordinary regular triflexagon with too many units, the problem sides
do, indeed become a 0![]() face. The production of this 0
face. The production of this 0![]() face is parallel to the flexing both backwards and frontwards at the same
time in the 3 unit proper tetraflexagon or order 4.
face is parallel to the flexing both backwards and frontwards at the same
time in the 3 unit proper tetraflexagon or order 4.
The flexagon with 0![]() faces of the double-hinge-position type may also
be considered as flexagons made of altered
faces of the double-hinge-position type may also
be considered as flexagons made of altered ![]() -gons, with alternate
-gons, with alternate
![]() -gon
vertices pushed in to form an
-gon
vertices pushed in to form an ![]() -gonal shape. Using this observation may
make the planning and manufacturing of this type of flexagon slightly
simpler, since they can then be treated exactly like other flexagons made
of altered leaves. Certain of the faces (to be determined in the usual way)
will, of course, be 0
-gonal shape. Using this observation may
make the planning and manufacturing of this type of flexagon slightly
simpler, since they can then be treated exactly like other flexagons made
of altered leaves. Certain of the faces (to be determined in the usual way)
will, of course, be 0![]() faces. In the same way as
faces. In the same way as ![]() vertices of these
leaves were forced flush with the others, so any kind of leaf can be
altered to give an assortment of 0
vertices of these
leaves were forced flush with the others, so any kind of leaf can be
altered to give an assortment of 0![]() face positions; by pushing in
one or more vertices.
face positions; by pushing in
one or more vertices.
As we have seen, the 0![]() face fits neatly in with the rest of our
flexagon theory. Just as 0
face fits neatly in with the rest of our
flexagon theory. Just as 0![]() faces can be used in conjunction with the
alteration of leaf shapes, so they can be applied to the other flexagon
``dimensions''. We will not, therefore, specifically mention 0
faces can be used in conjunction with the
alteration of leaf shapes, so they can be applied to the other flexagon
``dimensions''. We will not, therefore, specifically mention 0![]() faces,
to be distinguished from other faces, in the remainder of our discussion.
It is to be understood that they may be used in any possible situation
as desired.
faces,
to be distinguished from other faces, in the remainder of our discussion.
It is to be understood that they may be used in any possible situation
as desired.
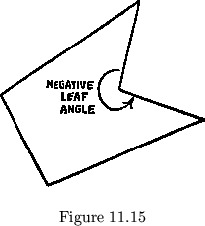
By pushing leaf vertices still further in toward the center of the
leaf, we can, for the first time, produce leaves with tangible negative
angles, which appear as concavities (See fig. 11.15). Previously,
negative angles have been produced only by continuously altering the leaf
angles through 0![]() . Now they are produced by passing through
0
. Now they are produced by passing through
0![]() faces, which have
leaf angles of 180
faces, which have
leaf angles of 180![]() . The only notable feature of these flexagons
is that they are exceedingly difficult to handle. Since the hinges,
when extended, cut the leaf, the leaf must be creased along the extension
for the flexagon to open out at all the faces. Also, due to the wide
variation in angles necessary to obtain negative angles, there tend to be
a large number of units, always a sign of instability.
. The only notable feature of these flexagons
is that they are exceedingly difficult to handle. Since the hinges,
when extended, cut the leaf, the leaf must be creased along the extension
for the flexagon to open out at all the faces. Also, due to the wide
variation in angles necessary to obtain negative angles, there tend to be
a large number of units, always a sign of instability.
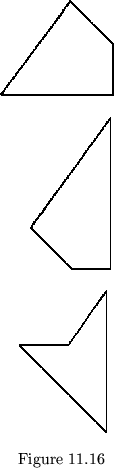
In the sign sequence we give the angles between pairs of consecutive leaf hinges. It can now be pointed out, however, that this information does not give the order of the hinge positions about the edge of the leaf. This order was determined so long as the leaves were assumed to be convex polygons. Now, though, a considerable variety of leaves may be used, all having the same sign sequences and maps in completely different-looking flexagons. For example, the leaves shown in fig. 11.16 all have same hinge positions, but in different order. The job of assigning an order to the hinge positions must be given to that old standby, the class, since the order of the hinges helps to determine the shapes of the leaves.