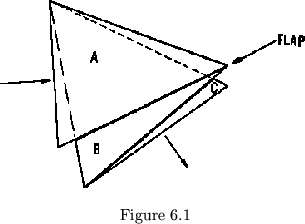
A pat is made up of two lesser inverted pats. The only reason for our limiting the number of lesser pats to two is that with any more, we run out of different places to hinge them together and are forced to use one spot twice. This causes a ``flap'' to appear, and the flexagon begins to fall apart. In fig. 6.1, for example, we have three subpats in one pat, in the pat structure 1 2 3. Since the triangles have room for only three non-overlying hinges, one of the four hinges will be superimposed (as at AB), creating the loose flap shown which is not usually permitted in flexagons 6.1. If, however, there were four positions for hinges, it would be possible to distribute the four hinges without causing flaps. Obviously, to have four positions we must use leaves with at least four edges.

Just as we passed from three-edged leaves and pats made of two
lesser pats to four-edged leaves and pats made up of three lesser pats,
so we can pass from n-gonal leaves and pats with (![]() ) subpats to
(
) subpats to
(![]() )-gonal leaves and pats made up of
)-gonal leaves and pats made up of ![]() subpats.
subpats.
Let us apply our theory to the construction of a flexagon constructed out of squares, and see how it works.
There are four possible positions around a given square at
which we can attach another square by a hinge. If we label these
positions clockwise
1-2-3-0, as in figure 6.2a, we can designate exactly
by which side a given square is hinged to another.
What we want to do is to hinge four squares together in such a
way that a given square is attached to two adjoining squares by only two
hinges and in such a way that each of the four hinge positions is used
only once. At the moment, we will consider the constant order
1234. We
will hinge leaf number 1 to leaf number 2 with the hinge in position
1, or the 1-hinge; 2 to 3 with the 2-hinge, and 3 to 4 with the 3-hinge.
We will leave the 0 position open, as it will hinge leaf 4 to leaf 1 in
the next unit (see figure 6.2b. What we have just constructed is only
one unit of a flexagon. The unit may be opened up so that leaf 1 is in
the left hand pat and leaves 2 through 4 are in the right hand pat. All
that is necessary in order to complete the flexagon is to add one more
identical unit, hinging the leaf numbered 1 of one unit to leaf 4 of the
other. If desired, an ![]() unit flexagon may be built, but those with more
than two units will not lie flat.
unit flexagon may be built, but those with more
than two units will not lie flat.

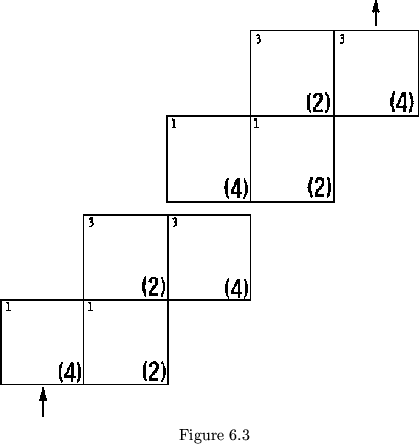
Thus far, the numbers we have given the leaves are pat structure
numbers. It will be convenient to number the leaves in such a way that
the number on the back of a leaf is one more or less than the number on
front, just as in the triflexagons. If we number the four leaves facing
up ``1'' and then fold the two pats of each unit together so that the unit
structure is
1; 2 3 4, then the leaves may be numbered
4-1 (4 on top, 1 underneath) 1-2, 2-3, 3-4; in order top to bottom.
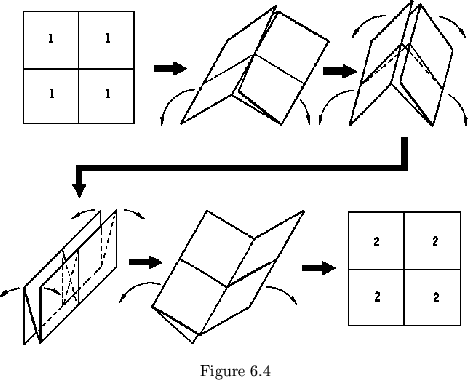
The resulting plan
is shown in figure 6.3; This flexagon may be flexed by grasping the two
units on the hinge or axis between them
(called the ``flexing axis''), with the
thumbs. The outside edges of the flexagon which are parallel to the flexing
axis are then pushed down, thus pinching
two adjacent pats together. The flexagon
may then be opened with the thumbs to the
new side (see figure 6.4). After flexing, the flexagon must be rotated
![]() and flexed along a new flexing axis. If we start at side 1, we find
that we can flex to 2, 3, 4 and back to 1 again in that order. By turning
the flexagon over, the order can be reversed
(4-3-2-1). We now see that
indeed, just as was predicted, we can make a flexagon that requires more
than three operations to complete the cycle 6.2.
and flexed along a new flexing axis. If we start at side 1, we find
that we can flex to 2, 3, 4 and back to 1 again in that order. By turning
the flexagon over, the order can be reversed
(4-3-2-1). We now see that
indeed, just as was predicted, we can make a flexagon that requires more
than three operations to complete the cycle 6.2.
Similarly, we may use a polygon of ![]() sides and, by hinging
to it
sides and, by hinging
to it ![]() congruent polygons consecutively in the hinge positions
1, 2, 3, - - - ,
congruent polygons consecutively in the hinge positions
1, 2, 3, - - - , ![]() ,
, ![]() and numbering as described for the square flexagon
and numbering as described for the square flexagon
![]() , we may obtain a unit of a flexagon requiring
, we may obtain a unit of a flexagon requiring
![]() flexes
to travel from a given face back to itself again without retracing the
path. The map of this flexagon may be represented by a polygon on
flexes
to travel from a given face back to itself again without retracing the
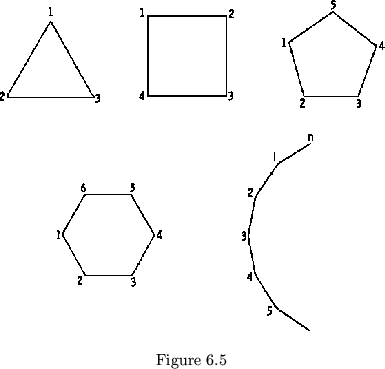
path. The map of this flexagon may be represented by a polygon on ![]() sides, as in figure 6.5. A flexagon which requires
sides, as in figure 6.5. A flexagon which requires ![]() flexings to return
to a given side will be called a ``cycle n'' flexagon, or just a plain
n-flexagon, it being convenient to read ``n-'' as the Greek prefix, tri-,
tetra-, penta-,..., octa-, for the 3 to 8 cycle flexagons. The flexagons
higher than cycle four will not lie flat since the sum of the angles
around the center for the two units combined will be greater than 360
flexings to return
to a given side will be called a ``cycle n'' flexagon, or just a plain
n-flexagon, it being convenient to read ``n-'' as the Greek prefix, tri-,
tetra-, penta-,..., octa-, for the 3 to 8 cycle flexagons. The flexagons
higher than cycle four will not lie flat since the sum of the angles
around the center for the two units combined will be greater than 360![]() .
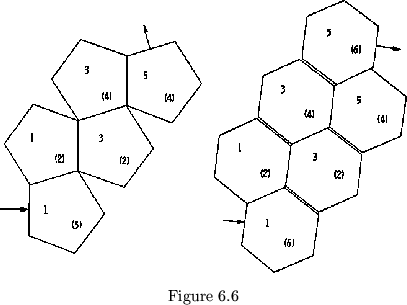
The plans for penta- and hexa- flexagons are shown in figure 6.6.
.
The plans for penta- and hexa- flexagons are shown in figure 6.6.
It should be noted also that the flexagons just discussed flex in such a way that the leaves are taken from the upper left and lower right pats (flexing axis held vertically) and are deposited on the upper right and lower left pats, respectively. It would be possible to make a flexagon which takes leaves from the upper right and lower left and deposits them on the upper left and lower right pats, respectively if the strip of polygons were wound
the other way--that is, hinged in the order 3 2 1 0 instead of 1 2 3 0 6.3.