If, after flexing a ![]() -flexagon of the kind described above
once, the same flexing axis is maintained, the flexagon will not flex
since there is but a single leaf in the left pat. This pat is joined
to the upper leaf of the right pat by a hinge in position
-flexagon of the kind described above
once, the same flexing axis is maintained, the flexagon will not flex
since there is but a single leaf in the left pat. This pat is joined
to the upper leaf of the right pat by a hinge in position ![]() , where
, where
![]() is the cycle of the flexagon. This single leaf in the left pat may,
however, be slit in the manner used with the tri-flexagons. That is,
another leaf may be hinged by a 1-hinge underneath the single
leaf 6.4.
is the cycle of the flexagon. This single leaf in the left pat may,
however, be slit in the manner used with the tri-flexagons. That is,
another leaf may be hinged by a 1-hinge underneath the single
leaf 6.4.
This allows a flex which will expose a new side. Note that the new
hinge must be in the ``one'' position, otherwise, the flexagon still will not
flex. In general, if the new side is added at side ![]() , having come from
side
, having come from
side ![]() , the new side will become
, the new side will become ![]() and the sides
and the sides
![]() (where
(where ![]() is the old order) must be renumbered
(the subscript refers to which of two cycles the side belongs). If we
now rotate the flexagon and attempt to flex, the flexagon instead opens
up using a set of hinges other than the 1-hinges and becomes a closed
strip of four polygons in which the hinges do not meet in the center.
This phenomenon is called tubulation. When an order five tetra-flexagon
tubulates, it resembles a cube with two opposite faces missing
(see figure 6.7a). A flexagon which is tubulating has the side
which was tubulated from,
is the old order) must be renumbered
(the subscript refers to which of two cycles the side belongs). If we
now rotate the flexagon and attempt to flex, the flexagon instead opens
up using a set of hinges other than the 1-hinges and becomes a closed
strip of four polygons in which the hinges do not meet in the center.
This phenomenon is called tubulation. When an order five tetra-flexagon
tubulates, it resembles a cube with two opposite faces missing
(see figure 6.7a). A flexagon which is tubulating has the side
which was tubulated from, ![]() , on the outside and another side,
, on the outside and another side,
![]() , on the inside. This relationship is shown on the map with
a dotted line drawn between the two sides as in figure 6.7b and c.
, on the inside. This relationship is shown on the map with
a dotted line drawn between the two sides as in figure 6.7b and c.
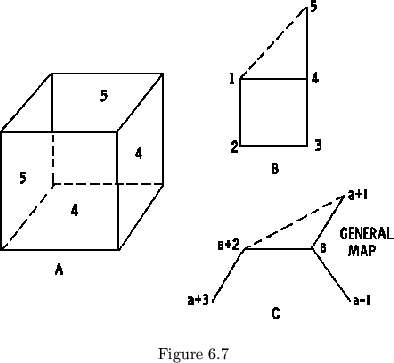
If the flexagon is turned over and
flexed back to ![]() it may then
either flex to
it may then
either flex to ![]() or tubulate
to
or tubulate
to ![]() , depending on whether the
flexagon was rotated or not before
flexing again. The operation of
tubulating is very much like that
of flexing, for it is seen that tubulating removes leaves from the left
pat and deposits them on the right pat. Indeed if the effective hinge,
that is, the hinge (not the zero-hinge) of each unit which is being
used for the operation, were in a one-position, the operation would be
a flex. If we were to cut the effective hinge used in this tubulation,
which in this case is in a
, depending on whether the
flexagon was rotated or not before
flexing again. The operation of
tubulating is very much like that
of flexing, for it is seen that tubulating removes leaves from the left
pat and deposits them on the right pat. Indeed if the effective hinge,
that is, the hinge (not the zero-hinge) of each unit which is being
used for the operation, were in a one-position, the operation would be
a flex. If we were to cut the effective hinge used in this tubulation,
which in this case is in a ![]() position, turn the flexagon inside
out and tape the hinge back together, we would have side
position, turn the flexagon inside
out and tape the hinge back together, we would have side ![]() on the
outside and side
on the
outside and side ![]() on the inside and could then close the tubulation,
open to side
on the inside and could then close the tubulation,
open to side ![]() , and flex back to side
, and flex back to side ![]() . This particular sequence
requires only three operations (flexings and tubulations) to return to a
given side without retracing a path, and thus may be looked upon as an
attempt by the flexagon to become a tri-flexagon. However, we do not
want to have to cut the hinge every time we run into a tubulation.
. This particular sequence
requires only three operations (flexings and tubulations) to return to a
given side without retracing a path, and thus may be looked upon as an
attempt by the flexagon to become a tri-flexagon. However, we do not
want to have to cut the hinge every time we run into a tubulation.
We want to have a complete cycle of ordinary flexes. We may do this in
the same manner as before, by slitting one of the leaves which is present
at the face ![]() ,
, ![]() . But in this case we find, oddly enough, that
there are three possible ways of doing so. First of all, having come
to side
. But in this case we find, oddly enough, that
there are three possible ways of doing so. First of all, having come
to side ![]() from side
from side ![]() , but after rotating and before the flexagon
is tubulated, there is a single leaf, which can be slit, in the right
hand pat. Also, tubulation removes all but a single leaf from the left
hand pat. The third possibility is the middle subpat. This may be slit,
in much the same manner as the single leaf. Slitting the right hand or
middle leaves produces a cycle with a mixture of right and left flexes
and will be considered in chapter 9. Any flexagon made so that it always
flexes left (or right if it is wound the other way) will be called a proper
flexagon. Any flexagon which does not flex consistently left or right
and whose subpats are not hinged consecutively
, but after rotating and before the flexagon
is tubulated, there is a single leaf, which can be slit, in the right
hand pat. Also, tubulation removes all but a single leaf from the left
hand pat. The third possibility is the middle subpat. This may be slit,
in much the same manner as the single leaf. Slitting the right hand or
middle leaves produces a cycle with a mixture of right and left flexes
and will be considered in chapter 9. Any flexagon made so that it always
flexes left (or right if it is wound the other way) will be called a proper
flexagon. Any flexagon which does not flex consistently left or right
and whose subpats are not hinged consecutively
![]() is an improper
flexagon. Since all our previous flexings have been from the left hand
pat, at the present we shall consider the slitting of only the single
left hand leaf arrived at after tubulating. If, after slitting this leaf
and numbering the new side we rotate and try to flex again, we find that
again the flexagon tubulates, this time using a
is an improper
flexagon. Since all our previous flexings have been from the left hand
pat, at the present we shall consider the slitting of only the single
left hand leaf arrived at after tubulating. If, after slitting this leaf
and numbering the new side we rotate and try to flex again, we find that
again the flexagon tubulates, this time using a ![]() 6.5 hinge. Now we
again have a number of choices for slitting the leaves, it is possible
not only to slit either the left or the right leaves, but to slit any
one of the subpats in between them, hinging the new side in a number 1
position. The subpats are for all intents and purposes single leaves in
this case. However, in order to be consistent, keeping the flexagon
proper and flexing left, we will choose to slit the left hand leaf.
Each successive time we slit, flex, and rotate, the hinge position of
the tubulation's effective hinge decreases by one. After
6.5 hinge. Now we
again have a number of choices for slitting the leaves, it is possible
not only to slit either the left or the right leaves, but to slit any
one of the subpats in between them, hinging the new side in a number 1
position. The subpats are for all intents and purposes single leaves in
this case. However, in order to be consistent, keeping the flexagon
proper and flexing left, we will choose to slit the left hand leaf.
Each successive time we slit, flex, and rotate, the hinge position of
the tubulation's effective hinge decreases by one. After ![]() slittings, the effective hinge will be a 1-hinge, and the flexagon will
flex normally through the new cycle. The new sides may be numbered in
succession counter-clockwise about the map
slittings, the effective hinge will be a 1-hinge, and the flexagon will
flex normally through the new cycle. The new sides may be numbered in
succession counter-clockwise about the map
![]() where
where ![]() is the cycle.
The other sides through side
is the cycle.
The other sides through side ![]() may
be renumbered, starting with
may
be renumbered, starting with ![]() . By the method just explained,
a cycle
. By the method just explained,
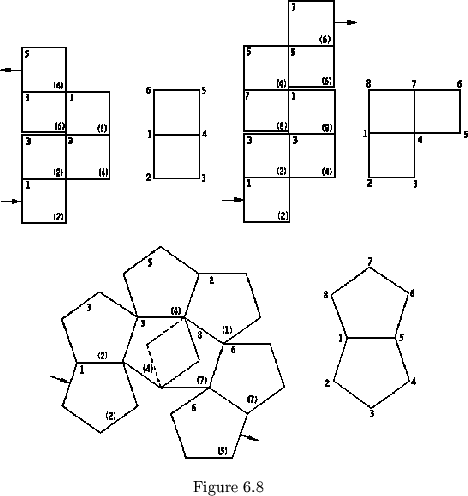
a cycle ![]() -flexagon of any order may be constructed. The map will be
made up of polygons with
-flexagon of any order may be constructed. The map will be
made up of polygons with ![]() sides, which will be joined to one another
by single edges (see figure 6.8).
sides, which will be joined to one another
by single edges (see figure 6.8).
The ability to tubulate is extremely important
and is deserving of extra study. If we add a new side by slitting the
single left hand leaf in a tubulating flexagon and hinging the new leaf
in a number one position, we find that we have not destroyed the tubulation
but rather we have hidden it by making it easier for the flexagon
to flex using a 1-hinge. This can be seen by clipping closed the side
which would normally turn up next in any given flexing operation. If
this if done the tubulation again appears. Tubulations which have been
concealed by the addition of new sides are called ``hidden'' tubulations,
while those which are a normal part of a series of flexes are called
``exposed'' tubulations. In any flexagon, there are hidden tubulations
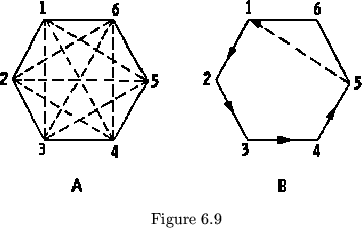
from any given side to every other non adjacent side of a given cycle.
These hidden tubulations may be shown in the map as in figure 6.9a but
since they clutter up the drawing, they are often omitted. Each
hidden tubulation from a given side to each non adjacent side uses a
different hinge. In all, there are ![]() possible tubulations using
possible tubulations using
![]() hinges originating at a given side. The hinges in positions 1
and
hinges originating at a given side. The hinges in positions 1
and ![]() , are used by forward and backward flexes respectively
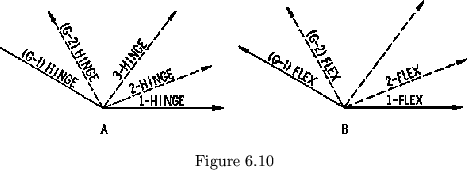
(see figure 6.10a). Furthermore these hidden tubulations may be considered
as short cuts for if the
tubulation were cut, turned inside
out, and normal flexing resumed,
one or more sides would be omitted
from the cycle (see figure 6.9b).
, are used by forward and backward flexes respectively
(see figure 6.10a). Furthermore these hidden tubulations may be considered
as short cuts for if the
tubulation were cut, turned inside
out, and normal flexing resumed,
one or more sides would be omitted
from the cycle (see figure 6.9b).
It is convenient to call all tubulations flexes and to give
them a number which corresponds to
the position of their effective hinges. Thus a normal flex which uses
a 1-hinge will be called a ``1-flex'' while a tubulation which uses
a 2-hinge will be called a ``2-flex'' and so on. The tubulation which
we first encountered in slitting leaves to add a new side (figure 6.7c)
was a ![]() -flex. The backward flex, which use a
-flex. The backward flex, which use a ![]() -hinge, is
a ``
-hinge, is
a ``![]() -flex'' (see figure 6.10b). The proper octaflexagon is a striking
proof that a tubulation should be considered a flex. The angle between
the input and output hinges in a 2-flex is 90
-flex'' (see figure 6.10b). The proper octaflexagon is a striking
proof that a tubulation should be considered a flex. The angle between
the input and output hinges in a 2-flex is 90![]() and in a two unit
flexagon the sum of the angles about the center is 360
and in a two unit
flexagon the sum of the angles about the center is 360![]() , so the
tubulating flexagon will lie flat. Furthermore, since the tubulating
flexagon does lie flat, it is not necessary to force the tubulation.
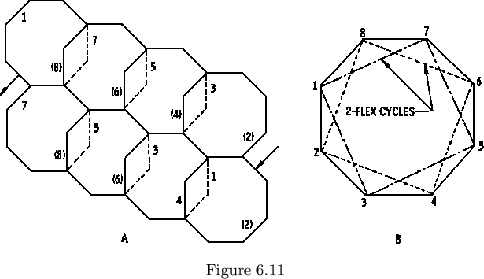
Two separate yet complete cycles of 2-flexes can be made,
the operation resembling very closely
that of 1-flexes in a tetraflexagon (see figure 6.11).
, so the
tubulating flexagon will lie flat. Furthermore, since the tubulating
flexagon does lie flat, it is not necessary to force the tubulation.
Two separate yet complete cycles of 2-flexes can be made,
the operation resembling very closely
that of 1-flexes in a tetraflexagon (see figure 6.11).