



Next: Conclusiones
Up: Dinámica de una red
Previous: Matriz de transferencia
Contents
Al igual que en el Capítulo anterior, si suponemos ahora
que los desplazamientos de dos partículas adyacentes forman
un Eigenvector de la Matriz de Transferencia, es decir, considerar
un segundo problema de eigenvalores de la forma
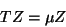 |
(II.26) |
se tiene que cada componente es multiplicada por el
factor 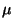 al ir de una partícula a otra sucesiva. Desde el
punto de vista físico, esto significa que dichos
Eigenvectores definen una descomposición de los desplazamientos
de las partículas de Ondas, cuya constante de propagación
es
al ir de una partícula a otra sucesiva. Desde el
punto de vista físico, esto significa que dichos
Eigenvectores definen una descomposición de los desplazamientos
de las partículas de Ondas, cuya constante de propagación
es 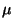 ; y como ella puede ser real, compleja o imaginaria, de
valor absoluto
; y como ella puede ser real, compleja o imaginaria, de
valor absoluto 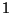 ó distinto de él, es posible distinguir la
propagación de las ondas, en forma exponencial creciente o
decreciente, de una manera oscilatoria o una mezcla,
respectivamente.
Muchas veces, como veremos en los capítulos que siguen, no es
más útil el logaritmo de
ó distinto de él, es posible distinguir la
propagación de las ondas, en forma exponencial creciente o
decreciente, de una manera oscilatoria o una mezcla,
respectivamente.
Muchas veces, como veremos en los capítulos que siguen, no es
más útil el logaritmo de 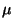 , es decir
, es decir
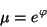 |
(II.27) |
y a 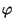 es lo que se conoce como Número de
Onda del Eigenvector
es lo que se conoce como Número de
Onda del Eigenvector 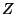 .
.




Next: Conclusiones
Up: Dinámica de una red
Previous: Matriz de transferencia
Contents
Pedro Hernandez
2006-02-20