


Next: Defecto en la constante
Up: Cadena con un defecto
Previous: Cadena con un defecto
Contents
Esta vez analizaremos el comportamiento de una red unidimensional,
cuando una de sus masas, la hacemos variar entre sus dos
límites posibles, es decir, desde un valor igual a cero,
hasta un valor muy grande y en el límite que tienda a infinito;
permaneciendo las demás masas constantes.
Consideremos que cada una de las masas de las partículas
de la cadena, tenga un valor igual a 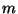 , excepto la
partícula
, excepto la
partícula 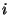 , que corresponde al defecto y que tiene un
valor
, que corresponde al defecto y que tiene un
valor 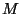 , también hacemos que todas las constantes de resorte
sean iguales a
, también hacemos que todas las constantes de resorte
sean iguales a 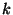 , en otras palabras, se trata de una cadena
homogénea con excepción de la partícula
, en otras palabras, se trata de una cadena
homogénea con excepción de la partícula 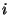 .
Si introducimos la notación
.
Si introducimos la notación
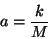 |
(III.28) |
la Matriz de Transferencia para la partícula 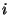 es
es
![\begin{displaymath}
\left[ \begin{array}{ccc}
\frac{\lambda + 2a}{a} & -1 \\
\\
1 & 0
\end{array} \right]
\end{displaymath}](img235.png) |
(III.29) |
para las demás partículas, todas las matrices
tienen la forma de (III.4).
Si suponemos que a la izquierda del defecto hay 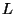 partículas y a la derecha
partículas y a la derecha  , como se muestra en la
figura siguiente
como siempre, se pueden tener distintas condiciones a la
frontera, pero en la parte anterior ya hemos visto el tratamiento
para las distintas clases de condiciones, entonces por ahora
supondremos que la cadena tiene extremos fijos. Así la
matríz que describe el movimiento de toda la red la podemos
escribir como
, como se muestra en la
figura siguiente
como siempre, se pueden tener distintas condiciones a la
frontera, pero en la parte anterior ya hemos visto el tratamiento
para las distintas clases de condiciones, entonces por ahora
supondremos que la cadena tiene extremos fijos. Así la
matríz que describe el movimiento de toda la red la podemos
escribir como
![\begin{displaymath}
\tau \left[ \begin{array}{ccc}
\frac{\lambda - a_{0}}{a_{1...
... a_{0}}{a_{1}} & -1 \\
\\
1 & 0
\end{array} \right]^{L}
\end{displaymath}](img239.png) |
(III.30) |
pero es posible escribir (III.29) como
![\begin{displaymath}
\left[ \begin{array}{ccc}
\frac{\lambda + 2a}{a} & -1 \\ ...
...y}{cc}
\varepsilon & 0 \\
\\
0 & 0
\end{array} \right]
\end{displaymath}](img240.png) |
(III.31) |
donde
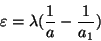 |
(III.32) |
sustituyendo (III.31) en (III.30) se tiene
Podemos evaluar fácilmente las potencias de las matrices
recordando que
se tiene entonces
donde la primera matriz, representa el comportamiento de
un segmento de la cadena original a la derecha del defecto, y la
segunda el de un segmento a la izquierda.
Haciendo uso de (III.16) y de las Ecs. de arriba,  tiene
la forma
tiene
la forma
entonces la condición que determina las frecuencias
para este modelo es
 |
(III.33) |
nuevamente como
es posible escribir (III.33) de la siguiente forma
finalmente si hacemos uso de (III.32) y de las expresiones para
 y
y  , la Ec. de arriba queda
, la Ec. de arriba queda
la interpretación que podemos hacer de la fracción
racional de arriba es la siguiente, las raíces del numerador
corresponden, salvo un factor, a las frecuencias de la cadena sin
modificaciones, y los ceros del denominador o polos de la
fracción corresponden a las frecuencias de tres cadenas, una con
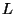 partículas, otra de
partículas, otra de  y la de la masa modificada.
Las intersecciones de la fracción racional y la constante que
aparece a la derecha de (III.33
y la de la masa modificada.
Las intersecciones de la fracción racional y la constante que
aparece a la derecha de (III.33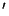 ) nos proporcionan las
frecuencias posibles para la red con un defecto en masa.
La fig. (3.1) nos muestra la gráfica de la función dada por
(III.33
) nos proporcionan las
frecuencias posibles para la red con un defecto en masa.
La fig. (3.1) nos muestra la gráfica de la función dada por
(III.33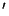 )
Si analizamos los dos límites posibles de
)
Si analizamos los dos límites posibles de 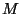 , es claro de
la gráfica, que cuando
, es claro de
la gráfica, que cuando 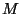 crece, las frecuencias disminuyen,
esto se debe a que todos los eigenvalores son negativos, que es un
resultado ya esperado, porque si aplicamos el Teorema de
Gerschgorin a nuestra matriz de movimiento, hallaremos que el
intervalo posible para nuestros eigenvalores es negativo. En el
límite cuando
crece, las frecuencias disminuyen,
esto se debe a que todos los eigenvalores son negativos, que es un
resultado ya esperado, porque si aplicamos el Teorema de
Gerschgorin a nuestra matriz de movimiento, hallaremos que el
intervalo posible para nuestros eigenvalores es negativo. En el
límite cuando
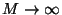 , las intersecciones de
la fracción racional y la constante, ocurren en los polos, lo
que nos indica que la cadena se separa en dos, con
, las intersecciones de
la fracción racional y la constante, ocurren en los polos, lo
que nos indica que la cadena se separa en dos, con 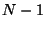 partículas en total y la masa modificada actúa como un
extremo confinante, además todas las frecuencias disminuyen a su
valor mínimo, y una de ellas en el límite tiende a cero.
Cuando la constante es cero, la intersección es precisamente
en las raíces que corresponden a la cadena sin
modificación, que es de esperarse ya que en este caso
partículas en total y la masa modificada actúa como un
extremo confinante, además todas las frecuencias disminuyen a su
valor mínimo, y una de ellas en el límite tiende a cero.
Cuando la constante es cero, la intersección es precisamente
en las raíces que corresponden a la cadena sin
modificación, que es de esperarse ya que en este caso 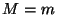 Finalmente si
Finalmente si
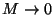 , las frecuencias van a aumentar
hasta un cierto valor que corresponderá a
, las frecuencias van a aumentar
hasta un cierto valor que corresponderá a 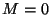 , ellas van a
estar dadas por la intesección de la asíntota
, ellas van a
estar dadas por la intesección de la asíntota 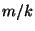 con la
fracción racional, excepto una frecuencia que tiende a ser
infinita.
En este último límite, desde el punto de vista
físico lo que sucede es que la partícula no existe,
entonces los dos resortes que originalmente estaban ligados a la
partícula se unen directamente, dando lugar a que un grado de
libertad se pierda y se tenga un resorte con constante
con la
fracción racional, excepto una frecuencia que tiende a ser
infinita.
En este último límite, desde el punto de vista
físico lo que sucede es que la partícula no existe,
entonces los dos resortes que originalmente estaban ligados a la
partícula se unen directamente, dando lugar a que un grado de
libertad se pierda y se tenga un resorte con constante 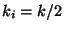 , lo anterior se puede mostrar si efectuamos el producto de
las tres siguientes Matrices de Transferencia
, lo anterior se puede mostrar si efectuamos el producto de
las tres siguientes Matrices de Transferencia
que corresponden a las partículas, vecina derecha
del defecto, el defecto y la vecina izquierda respectivamente. Se
encuentra que se obtiene el mismo resultado cuando hacemos 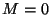 en el producto de arriba, que el de multiplicar las siguientes
matrices
en el producto de arriba, que el de multiplicar las siguientes
matrices
que representan a las partículas vecinas del
defecto unidas por una constante elástica 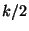 La ilustración de los resultados anteriores, de lo que sucede
en el espectro de una red unidimensional homogénea con un
defecto puntual en masa, para los dos límites posibles, lo
hace la Fig. (3.2), obtenida mediante la diagonalización de la
Matriz de Movimiento, variando la masa de la partícula 4 de
una red de 8 partículas, desde un valor pequeño hasta uno
grande; es clara la transición suave que ocurre entre los dos
límites del valor de la masa.
Desde el punto de vista físico, se espera que los Modos
Normales tengan el siguiente comportamiento: para el caso en que
La ilustración de los resultados anteriores, de lo que sucede
en el espectro de una red unidimensional homogénea con un
defecto puntual en masa, para los dos límites posibles, lo
hace la Fig. (3.2), obtenida mediante la diagonalización de la
Matriz de Movimiento, variando la masa de la partícula 4 de
una red de 8 partículas, desde un valor pequeño hasta uno
grande; es clara la transición suave que ocurre entre los dos
límites del valor de la masa.
Desde el punto de vista físico, se espera que los Modos
Normales tengan el siguiente comportamiento: para el caso en que
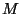 es muy pequeña, se pierde un grado de libertad, entonces se
tiene un Modo Normal, llamado localizado en el defecto, cuya
frecuencia es muy grande y en el límite llega a ser infinita;
en tal límite sólo la partícula ligera se excita. Para
los otros modos, el desplazamiento de la partícula es un
promedio del que tienen sus vecinos.
En el otro límite, es decir, cuando
es muy pequeña, se pierde un grado de libertad, entonces se
tiene un Modo Normal, llamado localizado en el defecto, cuya
frecuencia es muy grande y en el límite llega a ser infinita;
en tal límite sólo la partícula ligera se excita. Para
los otros modos, el desplazamiento de la partícula es un
promedio del que tienen sus vecinos.
En el otro límite, es decir, cuando 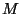 es muy grande,
difícilmente se mueve la partícula, dando lugar a que la
cadena se divida en dos, las cuales tienen un extremo confinado
debido a la inmovilidad de la partícula a la que estan
unidas, y para la frecuencia muy baja, el modo correspondiente es
aquel en el que la partícula hace que las demás
partículas vibren como ella lo hace.
es muy grande,
difícilmente se mueve la partícula, dando lugar a que la
cadena se divida en dos, las cuales tienen un extremo confinado
debido a la inmovilidad de la partícula a la que estan
unidas, y para la frecuencia muy baja, el modo correspondiente es
aquel en el que la partícula hace que las demás
partículas vibren como ella lo hace.
Figura 3.2:
Gráfica del negativo del cuadrado de las frecuencias
naturales de una cadena homogenea de 8 partículas, en la que
se modifica sistemáticamente la masa de la partícula 4, donde
el eje Y corresponde a dicho parametro.
|
|
Después de haber diagonalizado la Matriz de Movimiento, se
han obtenido los eigenvectores correspondientes, La fig. (3.3) nos
muestra la gráfica en perspectiva de todos ellos, donde el eje
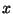 corresponde al número de partículas, la parte
``negativa'' de y es la variación del parámetro, esta vez la
variación de la masa de una de las partículas, y el eje
corresponde al número de partículas, la parte
``negativa'' de y es la variación del parámetro, esta vez la
variación de la masa de una de las partículas, y el eje 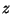 nos represente la amplitud de vibración.
Las gráficas ilustran el comportamiento esperado y que se ha
descrito arriba, se observa también la transición suave que
existe en los Modos al pasar de un límite al otro, empezando
por el menor y ascendiendo hasta llegar al límite alto,
pasando por el comportamiento de una cadena homogénea, que
ocurre en el centro de cada Modo; a la izquierda se tienen los
Modos Opticos en orden descendente y a la derecha se muestran los
Acústicos en el mismo orden.
En el Apéndice A, se describen brevemente y se muestran los
listados de las Subrutinas empleadas para diagonalizar las
distintas Matrices que nos representan los diferentes modelos de
cadenas, y además para obtener los correspondientes
Eigenvectores. En el B se tiene el listado de un Programa
Principal llamado TRIIR y las diferentes subrutinas empleadas para
obtener las gráficas de los Modos Normales, es único y fué
utilizado para todos los Modelos .
Finalmente en el C el Programa Principal llamado TRIVM, que
hace las variaciones en la masa.
nos represente la amplitud de vibración.
Las gráficas ilustran el comportamiento esperado y que se ha
descrito arriba, se observa también la transición suave que
existe en los Modos al pasar de un límite al otro, empezando
por el menor y ascendiendo hasta llegar al límite alto,
pasando por el comportamiento de una cadena homogénea, que
ocurre en el centro de cada Modo; a la izquierda se tienen los
Modos Opticos en orden descendente y a la derecha se muestran los
Acústicos en el mismo orden.
En el Apéndice A, se describen brevemente y se muestran los
listados de las Subrutinas empleadas para diagonalizar las
distintas Matrices que nos representan los diferentes modelos de
cadenas, y además para obtener los correspondientes
Eigenvectores. En el B se tiene el listado de un Programa
Principal llamado TRIIR y las diferentes subrutinas empleadas para
obtener las gráficas de los Modos Normales, es único y fué
utilizado para todos los Modelos .
Finalmente en el C el Programa Principal llamado TRIVM, que
hace las variaciones en la masa.



Next: Defecto en la constante
Up: Cadena con un defecto
Previous: Cadena con un defecto
Contents
Pedro Hernandez
2006-02-20
![\begin{displaymath}
\left[ \begin{array}{ccc}
\frac{\lambda + 2a}{a} & -1 \\
\\
1 & 0
\end{array} \right]
\end{displaymath}](img235.png)
![\includegraphics[width=5in]{f03p43.eps}](img238.png)
![\begin{displaymath}
\tau \left[ \begin{array}{ccc}
\frac{\lambda - a_{0}}{a_{1...
... a_{0}}{a_{1}} & -1 \\
\\
1 & 0
\end{array} \right]^{L}
\end{displaymath}](img239.png)
![\begin{displaymath}
\left[ \begin{array}{ccc}
\frac{\lambda + 2a}{a} & -1 \\ ...
...y}{cc}
\varepsilon & 0 \\
\\
0 & 0
\end{array} \right]
\end{displaymath}](img240.png)
![\begin{displaymath}
\tau = \left[ \begin{array}{cc}
\frac{\lambda - a_0}{a_1} ...
...- a_0}{a_1} & -1 \\
& \\
1 & 0
\end{array} \right]^{L}
\end{displaymath}](img242.png)
![\begin{displaymath}
\left[ \begin{array}{ccc}
\frac{\lambda - a_0}{a_1} & -1 ...
...hi & -\mbox{senh} \ (N - L - 2)
\varphi
\end{array} \right]
\end{displaymath}](img244.png)
![\begin{displaymath}
\left[ \begin{array}{ccc}
\frac{\lambda - a_0}{a_1} & -1 ...
... \varphi & -\mbox{senh} \ (L - 1)\varphi
\end{array} \right]
\end{displaymath}](img245.png)
![\begin{displaymath}
\tau = \frac{1}{\mbox{senh}} \ \varphi \left[ \begin{array}...
...varphi & -\mbox{senh} \ (N + 1)
\varphi
\end{array} \right]
\end{displaymath}](img246.png)
![\begin{displaymath}
\frac{+ \epsilon}{\mbox{senh}^{2} \ \varphi} \left[
\begin...
...L-1) \ \varphi \ \mbox{senh} L \ \varphi
\end{array} \right]
\end{displaymath}](img247.png)
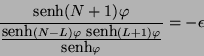
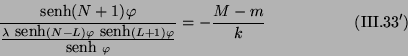
![\begin{displaymath}
\left[ \begin{array}{cc}
\frac{M}{k}\lambda + 2 & -1 \\
...
...c{m}{k}\lambda + 2 & -1 \\
\\
1 & 0
\end{array} \right]
\end{displaymath}](img261.png)
![\begin{displaymath}
\left[ \begin{array}{cc}
\frac{m}{k}\ \ \lambda+ \frac{1}...
...}{k}\lambda + 2 +1 & -2 \\
\\
1 & 0
\end{array} \right]
\end{displaymath}](img262.png)