



Next: Cadena diatómica
Up: Cadena con un defecto
Previous: Defecto en masa
Contents
Ahora deseamos hacer una modificación similar a la del caso
anterior, sólo que ahora es en una de las constantes
elásticas, esta vez también tenemos dos límites posibles,
uno cuando
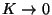 y el otro cuando
y el otro cuando
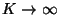 .
Nuevamente consideramos una cadena homogénea con extremos
fijos, excepto por la liga que une a las partículas
.
Nuevamente consideramos una cadena homogénea con extremos
fijos, excepto por la liga que une a las partículas 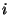 e
e 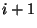 , que tiene un valor distinto al de las demás, denotémos
por
, que tiene un valor distinto al de las demás, denotémos
por
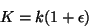 |
(III.34) |
así las Matrices de Transferencia para dichas
partículas son
y
si las denotamos por 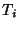 y
y 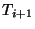 respectivamente, es posible escribirlas de la siguiente forma
respectivamente, es posible escribirlas de la siguiente forma
y
observamos que la primera parte de cada una de las
Matrices de arriba, corresponde a una partícula perteneciente
a una cadena homogénea; efectuemos el producto 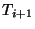
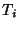
finalmente
si a la primera parte la denotamos por 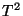 y a la
segunda por
y a la
segunda por 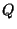 , en forma concisa queda
, en forma concisa queda
Así 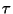 esta vez tiene la forma
esta vez tiene la forma
o también
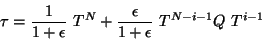 |
(III.35) |
la Ec. de Eigenvalores en este caso es
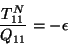 |
(III.36) |
donde 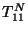 es el elemento (1,1) de
es el elemento (1,1) de 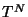 y
y
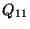 de
de
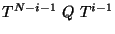 Nuevamente tenemos una fracción racional igual a una
constante, donde las raíces del numerador corresponden a las
de una cadena homogénea de
Nuevamente tenemos una fracción racional igual a una
constante, donde las raíces del numerador corresponden a las
de una cadena homogénea de 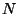 partículas y las
partículas y las 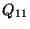 a
las de una con
a
las de una con 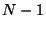 , una de las cuales tiene como masa la suma de
las dos, estas originalmente estaban ligados por el resorte
modificado. Como antes las frecuencias posibles para este modelo,
están dadas por las intersecciones de la fraccón racional y la
constante
, una de las cuales tiene como masa la suma de
las dos, estas originalmente estaban ligados por el resorte
modificado. Como antes las frecuencias posibles para este modelo,
están dadas por las intersecciones de la fraccón racional y la
constante 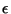 .
La fig. (3.4) muestra el comportamiento de las frecuencias para
este defecto.
El análisis de la gráfica muestra que cuando
.
La fig. (3.4) muestra el comportamiento de las frecuencias para
este defecto.
El análisis de la gráfica muestra que cuando
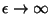 , las intersecciones de las curvas son tales
que todas, menos una, se acercan a los polos, que corresponden a
las frecuencias de una cadena con
, las intersecciones de las curvas son tales
que todas, menos una, se acercan a los polos, que corresponden a
las frecuencias de una cadena con 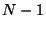 partículas, donde una
de ellas tiene una masa igual al doble de la original, que era de
esperarse ya que físicamente el resorte va a a ser
inextensible, y entonces las partículas que liga se comportan
como si fuera una sóla; arriba mencionamos que una no se
acercaba a un polo, ya que de la gráfica vemos que tiende a
infinito.
Cuando
partículas, donde una
de ellas tiene una masa igual al doble de la original, que era de
esperarse ya que físicamente el resorte va a a ser
inextensible, y entonces las partículas que liga se comportan
como si fuera una sóla; arriba mencionamos que una no se
acercaba a un polo, ya que de la gráfica vemos que tiende a
infinito.
Cuando 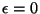 las intersecciones corresponden a las
raices de una cadena homogénea.
Finalmente si
las intersecciones corresponden a las
raices de una cadena homogénea.
Finalmente si
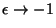 , lo cual implica que no
exista el enlace, la cadena se separa en dos partes, solo que
ahora tiene extremos libres donde la liga ha desaparecido, si en
el otro extremo las frecuencias crecían, ahora decrecen hasta
su valor mínimo, fisicamente válido, ya que a diferencia
del defecto en masa, ninguna de las frecuencias hace cero, en
ninguno de los dos límites.
La fig (3.5) nos ilustra los resultados mencionados arriba, se
obtuvo diagonalizando la matriz de movimiento directamente,
variando esta vez la constante de resorte entre las
partículas 3 y 4 para una red de 8 partículas; se
observa la misma transición suave de antes entre los dos
extremos, sólo que la gráfica es la negativa de la real.
, lo cual implica que no
exista el enlace, la cadena se separa en dos partes, solo que
ahora tiene extremos libres donde la liga ha desaparecido, si en
el otro extremo las frecuencias crecían, ahora decrecen hasta
su valor mínimo, fisicamente válido, ya que a diferencia
del defecto en masa, ninguna de las frecuencias hace cero, en
ninguno de los dos límites.
La fig (3.5) nos ilustra los resultados mencionados arriba, se
obtuvo diagonalizando la matriz de movimiento directamente,
variando esta vez la constante de resorte entre las
partículas 3 y 4 para una red de 8 partículas; se
observa la misma transición suave de antes entre los dos
extremos, sólo que la gráfica es la negativa de la real.
Figura 3.5:
Gráfica del negativo del cuadrado de las frecuencias de resonancia
de una cadena homogenea de 8 partículas, en la que se modifica
sistemáticamente la k entre las partículas 3 y 4, la variación
es en el eje vertical.
|
|
En el apéndice D se muestra el listado del programa principal
diseñado para hacer la variación en la constante elástica,
cuyo nombre es TRIVK:
Como antes, también se obtuvieron los Modos Normales y se
graficaron, la Fig. (3.6) nos muestra el comportamiento de la
cadena para esta clase de defecto, podemos observar que cuando
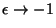 , que ocurre en cada una de las partes
inferiores de las figuras pequeñas, la separacón de la cadena
en 2 completamente independientes, ya que éstas tienen ahí
un extremo libre.
Cuando
, que ocurre en cada una de las partes
inferiores de las figuras pequeñas, la separacón de la cadena
en 2 completamente independientes, ya que éstas tienen ahí
un extremo libre.
Cuando
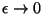 , el comportamiento es el de una
cadena homogénea y ocurre en la parte media de cada figura.
Finalmente cuando
, el comportamiento es el de una
cadena homogénea y ocurre en la parte media de cada figura.
Finalmente cuando
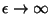 , esta vez el
comportamiento se observa en las partes superiores, se ve que en
el modo de más alta frecuencia, que es el de esquina superior
derecha, las partículas unidas por el resorte, vibran en
direcciones opuestas y las demás, no efectuan ningun movimiento,
éste es el llamado Modo localizado en el defecto; en los demás
modos las masas ligadas por el resorte inextensible se comportan
como una sóla.
También vemos la transición suave en los Modos entre los
dos límites extremos, pasando por el comportamiento de una
cadena homogénea, en las partes medias de cada uno.
Los Modos están ordenados en la figura en orden descendente,
los de la derecha son los Opticos y los de la izquierda los
Acústicos.
Aún cuando en ambos casos hemos derivado las Ecs. para
cadenas homogéneas con un defecto para simplificar el álgebra,
es claro, que los resultados son válidos para una cadena
inhomogénea, masas y resortes con valores diferentes pero que al
hacer la variación del defecto permanecen cons-tantes, sólo
que como hemos repetido muchas veces, ahora la matriz que nos
proporciona el comportamiento no es la potencia de una matriz sino
un producto de todas las distintas matrices de transferencia.
, esta vez el
comportamiento se observa en las partes superiores, se ve que en
el modo de más alta frecuencia, que es el de esquina superior
derecha, las partículas unidas por el resorte, vibran en
direcciones opuestas y las demás, no efectuan ningun movimiento,
éste es el llamado Modo localizado en el defecto; en los demás
modos las masas ligadas por el resorte inextensible se comportan
como una sóla.
También vemos la transición suave en los Modos entre los
dos límites extremos, pasando por el comportamiento de una
cadena homogénea, en las partes medias de cada uno.
Los Modos están ordenados en la figura en orden descendente,
los de la derecha son los Opticos y los de la izquierda los
Acústicos.
Aún cuando en ambos casos hemos derivado las Ecs. para
cadenas homogéneas con un defecto para simplificar el álgebra,
es claro, que los resultados son válidos para una cadena
inhomogénea, masas y resortes con valores diferentes pero que al
hacer la variación del defecto permanecen cons-tantes, sólo
que como hemos repetido muchas veces, ahora la matriz que nos
proporciona el comportamiento no es la potencia de una matriz sino
un producto de todas las distintas matrices de transferencia.




Next: Cadena diatómica
Up: Cadena con un defecto
Previous: Defecto en masa
Contents
Pedro Hernandez
2006-02-20
![\begin{displaymath}
\left[ \begin{array}{ccc}
\frac{\frac{\lambda-a_{0}}{a_{1...
...
& \\
1 & 0
\end{array} \right] \qquad \mbox{para la } i
\end{displaymath}](img271.png)
![\begin{displaymath}
\left[ \begin{array}{ccc}
\frac{\lambda-a_{0}}{a_{1}} + \...
...
& \\
1 & 0
\end{array} \right] \qquad \mbox{para } i + 1
\end{displaymath}](img272.png)
![\begin{displaymath}
T_{i} = \frac{1}{1+\epsilon} \left[ \begin{array}{ccc}
\fr...
...ft[ \begin{array}{ccc}
1 & 0 \\
1 & 0
\end{array} \right]
\end{displaymath}](img273.png)
![\begin{displaymath}
T_{i + 1} = \left[ \begin{array}{ccc}
\frac{\lambda-a_{0}}...
...{array}{ccc}
1 & -1 \\
& \\
0 & 0
\end{array} \right]
\end{displaymath}](img274.png)
![\begin{displaymath}
T_{i + 1} \ \ T_{i} = \left(\left[ \begin{array}{ccc}
\fra...
...}{ccc}
1 & 0 \\
& \\
1 & 0
\end{array} \right]\right)
\end{displaymath}](img275.png)
![\begin{displaymath}
\quad = \frac{1}{1+\epsilon} \left[ \begin{array}{ccc}
\fr...
...n{array}{ccc}
0 & 0 \\
& \\
0 & 0
\end{array} \right]
\end{displaymath}](img276.png)
![\begin{displaymath}
T_{i+1} \ T_{i} = \frac{1}{1+\epsilon} \left[ \begin{array}...
..._{0})}{a_{1}}-2 & -1 \\
& \\
1 & 0
\end{array} \right]
\end{displaymath}](img277.png)