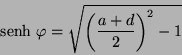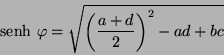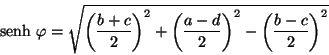


Next: Expresiones para el producto
Up: Diversos aspectos de la
Previous: Diversos aspectos de la
Contents
En el estudio de vibraciones de redes unidimensionales, que
hemos hecho en los capítulos anteriores, hemos visto que
las Matrices de Transferencia son de dimensión dos, y que para
el caso general de una cadena inhomogénea la matriz era
cuyo determinante es
no se pierde generalidad si uno factoriza la matriz
en tal forma que el determinante de  sea uno, ya que el
estudio que iniciamos en este último capítulo, es el de la
Representación Geométrica de las llamadas Matrices
unimodulares de dimensión dos, que se definen como aquellas,
que cumplen la siguiente condición.
sea uno, ya que el
estudio que iniciamos en este último capítulo, es el de la
Representación Geométrica de las llamadas Matrices
unimodulares de dimensión dos, que se definen como aquellas,
que cumplen la siguiente condición.
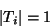 |
(IV.1) |
para el caso en que todas las constantes elásticas
sean las mismas la Ec. (IV.I) se cumple trivialmente.
De una forma completamente general consideremos la siguiente
matriz de dimensión dos
que tiene la propiedad de Unimodularidad, es decir
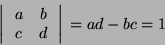 |
(IV.2) |
su Ec. característica es
explícitamente
de (IV.2) es posible escribirla como
es claro que los eigenvalores son recíprocos
entre sí, ellos son
si hacemos la sustitución usual
finalmente se obtienen
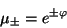 |
(IV.3) |
Ahora calculemos los eigenvectores correspondientes, los
derechos son
de donde
Los eigenvectores izquierdos son
así
Como nos interesa obtener cierta función de 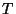 , primero
debemos aplicar el Teorema Espectral y para ello necesitamos los
Operadores de Proyección correspondientes, por lo que haremos
uso de las expresiones obtenidas en el Capítulo anterior y
que eran
, primero
debemos aplicar el Teorema Espectral y para ello necesitamos los
Operadores de Proyección correspondientes, por lo que haremos
uso de las expresiones obtenidas en el Capítulo anterior y
que eran
![\begin{displaymath}
P_{\pm} = \frac{\left[ \begin{array}{ccc}
\upsilon_{\pm} &...
...& \nu_{\pm}
\end{array} \right]}{\nu_{\pm} + \upsilon_{\pm}}
\end{displaymath}](img373.png) |
(IV.4) |
calculando las expresiones necesarias
pero
entonces
finalmente
ahora la expresión
haciendo uso de la expresión para el determinante de
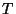
finalmente
sustituyendo todas las expresiones obtenidas en (IV.4)
se tiene
o también
aplicando ahora sí el Teorema Espectral se obtiene
![\begin{displaymath}
T = \frac{\mu_{+}}{2\mbox{senh} \ \varphi} \left[
\begin{a...
...mu_{-} - d & b \\
\\
c & \mu_{-}- a
\end{array} \right]
\end{displaymath}](img384.png) |
(IV.5) |
Para obtener 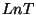 aplicamos el Teorema de Sylvester y hacemos uso
de (IV.3), con lo que se obtiene
aplicamos el Teorema de Sylvester y hacemos uso
de (IV.3), con lo que se obtiene
como
entonces
finalmente
![\begin{displaymath}
L_{n} \ T = \frac{\varphi}{2\mbox{senh} \ \varphi} \left[
...
...d}{2} & b \\
\\
c & \frac{d - a}{2}
\end{array} \right]
\end{displaymath}](img390.png) |
(IV.6) |
Si se defienen las siguientes Matrices
es posible escribir (IV.6) como
Ahora bien, si definimos la matriz
![\begin{displaymath}
U = \frac{(b + c)}{2} \ J + \frac{(a - d)}{2} \ K + \frac{(...
...d}{2} & b \\
\\
c & \frac{d - a}{2}
\end{array} \right]
\end{displaymath}](img394.png) |
(IV.7) |
donde 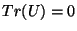
De la expresión para las raíces y la definición del
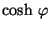 ,
se tiene
,
se tiene
sustituyendo la relación (IV.2) queda
con un poco de álgebra se llega a la expresión
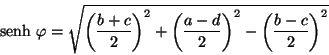 |
(IV.8) |
si examinamos (IV.7) es claro que (IV.8) corresponde a
una pseudonorma de  denominada de Lorentz en tres dimensiones,
efectuando de una nueva definición
denominada de Lorentz en tres dimensiones,
efectuando de una nueva definición
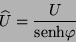 |
(IV.9) |
finalmente se tiene
![\begin{displaymath}
\left[ \begin{array}{ccc}
a & b \\
c & d
\end{array} \right] = e^{\varphi \widehat{U}}
\end{displaymath}](img402.png) |
(IV.10) |
o
las Ecs. de arriba implican que siempre es posible
escribir cualquier Matriz Unimodular de dimensión 2, como una
combinación lineal de las Matrices  y
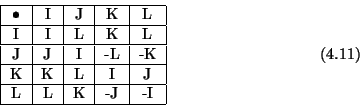
y 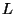 . Estas tienen
la siguiente tabla de multiplicación, que nos será muy útil
en lo que sigue
. Estas tienen
la siguiente tabla de multiplicación, que nos será muy útil
en lo que sigue
es conveniente hacer uso de esta base, ya que ademas de
que simplifican el álgebra, su determinante es distinto de cero;
porque a veces es común utilizar las siguientes matrices como
base pero son Singulares



Next: Expresiones para el producto
Up: Diversos aspectos de la
Previous: Diversos aspectos de la
Contents
Pedro Hernandez
2006-02-20
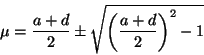
![\begin{displaymath}
P_{\pm} = \frac{\left[ \begin{array}{ccc}
\upsilon_{\pm} &...
...& \nu_{\pm}
\end{array} \right]}{\nu_{\pm} + \upsilon_{\pm}}
\end{displaymath}](img373.png)
![\begin{displaymath}
P_{\pm} = \pm \frac{b}{2\mbox{senh} \ \varphi} \left[
\beg...
...\
\frac{c}{b} & \frac{\mu_{\pm}- a}{b}
\end{array} \right]
\end{displaymath}](img382.png)
![\begin{displaymath}
T = \frac{\mu_{+}}{2\mbox{senh} \ \varphi} \left[
\begin{a...
...mu_{-} - d & b \\
\\
c & \mu_{-}- a
\end{array} \right]
\end{displaymath}](img384.png)
![\begin{displaymath}
L_{n} \ T = \frac{\varphi}{2\mbox{senh} \ \varphi} \left[
...
...d}{2} & b \\
\\
c & \frac{d - a}{2}
\end{array} \right]
\end{displaymath}](img390.png)
![\begin{displaymath}
U = \frac{(b + c)}{2} \ J + \frac{(a - d)}{2} \ K + \frac{(...
...d}{2} & b \\
\\
c & \frac{d - a}{2}
\end{array} \right]
\end{displaymath}](img394.png)
![]() ,
se tiene
,
se tiene