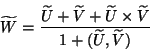


Next: Representación geométrica
Up: Diversos aspectos de la
Previous: Representación vectorial de las
Contents
Sean las siguientes Matrices Unimodulares expresadas en la
forma obtenida anteriormente
calculemos su producto
utilizando la tabla (IV.11) y agrupando los
términos como coeficientes de las matrices base, se tiene
ahora bien, si escribimos de la siguiente forma a las
matrices  y
y 
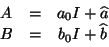 |
(IV.12) |
de los resultados de arriba es posible definir un
``producto interior'' que corresponde al coeficiente de 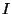 , que
difiere del producto interior usual en que existe un término con
signo negativo, lo que va a implicar que tengamos una métrica
distinta de la ordinaria; en función de los ``vectores''
, que
difiere del producto interior usual en que existe un término con
signo negativo, lo que va a implicar que tengamos una métrica
distinta de la ordinaria; en función de los ``vectores''
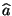 y
y 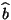 , el producto interior se define como
, el producto interior se define como
 |
(IV.13) |
También es posible definir un producto vectorial que
también difiere del ordinario en el signo del coeficiente
correspondiente a la matriz 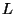 , explícitamente para los
vectores
, explícitamente para los
vectores 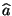 y
y 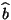 se tiene
se tiene
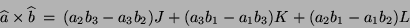 |
(IV.14) |
con todo lo anterior ya es posible efectuar el producto
de 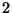 matrices representadas en forma exponencial, ya que estamos
interesados en ver como se combinan los exponentes, éstas son
matrices representadas en forma exponencial, ya que estamos
interesados en ver como se combinan los exponentes, éstas son
efectuando el producto
como 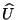 y
y 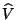 no tienen coeficiente
para
no tienen coeficiente
para 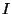 , es posible expresar el producto de ellas a partir de las
definiciones (IV.13) y (IV.14), es decir
, es posible expresar el producto de ellas a partir de las
definiciones (IV.13) y (IV.14), es decir
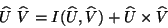 |
(IV.15) |
se tiene entonces
si se define
comparando coeficientes con el primer resultado, se
tiene que
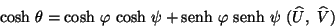 |
(IV.16) |
si hacemos analogía con trigonometría
esférica podemos decir que (IV.15) es la relación para el
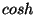 de la suma de dos ángulos en trigonometría
hiperbólica, ya que ahora estamos tratando con funciones
trigonométricas hiperbólicas, la cual nos implica que no
podemos, al multiplicar las exponenciales, sumar simplemente los
ángulos para obtener el ángulo resultante.
Para la parte vectorial se tiene
de la suma de dos ángulos en trigonometría
hiperbólica, ya que ahora estamos tratando con funciones
trigonométricas hiperbólicas, la cual nos implica que no
podemos, al multiplicar las exponenciales, sumar simplemente los
ángulos para obtener el ángulo resultante.
Para la parte vectorial se tiene
![\begin{displaymath}\mbox{tanh} \ \theta \ \widehat{W} =
\frac{\mbox{cosh} \ \va...
...phi \ \mbox{tanh} \ \psi \
(\widehat{U} \times \widehat{V})]
\end{displaymath}](img428.png) |
(IV.17) |
es conveniente efectuar una definición más
en términos de 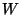
de la misma forma
 |
(IV.19) |
sustituyéndolas en (IV.16) se tiene
finalmente
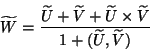 |
(IV.20) |
Las Ecs. (IV.16) y (IV.20) son las expresiones que nos permiten
el cálculo del producto de dos Matrices Unimodulares en esta
representación.



Next: Representación geométrica
Up: Diversos aspectos de la
Previous: Representación vectorial de las
Contents
Pedro Hernandez
2006-02-20
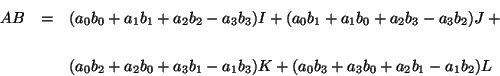
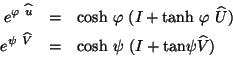
![\begin{eqnarray*}
e^{\psi \ \widehat{V}} e^{\psi \ \widehat{V}} & = &[\mbox{cos...
...h} \ \varphi \ \mbox{tanh} \ \psi \
\widehat{U} \ \widehat{V}]
\end{eqnarray*}](img420.png)
![\begin{eqnarray*}
e^{\varphi \ \widehat{U}} \ e^{\psi \ \widehat{V}} &=&
I[\m...
...arphi \ \mbox{tanh} \ \psi \
(\widehat{U} \times \widehat{V})]
\end{eqnarray*}](img424.png)