



Next: Matriz de transferencia
Up: Breve análisis de vibraciones
Previous: Breve análisis de vibraciones
Contents
Consideremos una cadena lineal de 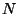 masas ligadas por resortes,
en la que existen ligas de cada una de las partículas hasta
con su K-ésimo vecino, y se supone que únicamente existen este
tipo de fuerzas, la figura nos muestra dicha cadena, que puede
tener sus extremos confinados, libres o una combinación.
si asumimos que la Ley de Hooke es válida, es decir,
las amplitudes de vibración son pequeñas, la ecuación de
movimiento para la partícula
masas ligadas por resortes,
en la que existen ligas de cada una de las partículas hasta
con su K-ésimo vecino, y se supone que únicamente existen este
tipo de fuerzas, la figura nos muestra dicha cadena, que puede
tener sus extremos confinados, libres o una combinación.
si asumimos que la Ley de Hooke es válida, es decir,
las amplitudes de vibración son pequeñas, la ecuación de
movimiento para la partícula 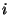 es
es
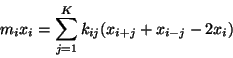 |
(I.1) |
donde 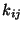 corresponde a la constante de resorte que
liga a las partículas
corresponde a la constante de resorte que
liga a las partículas 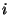 y
y 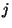 ,
, 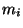 es la masa de la
partícula
es la masa de la
partícula 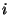 y
y 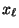 es el desplazamiento que sufre la
partícula
es el desplazamiento que sufre la
partícula 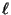 , que en todo el análisis lo consideraremos
como un desplazamiento transversal, ya que en principio, el
tratamiento de este tipo de desplazamientos y los longitudinales
es el mismo.
Sólo que la validez de esta ecuación, está limitada para los
valores de
, que en todo el análisis lo consideraremos
como un desplazamiento transversal, ya que en principio, el
tratamiento de este tipo de desplazamientos y los longitudinales
es el mismo.
Sólo que la validez de esta ecuación, está limitada para los
valores de 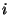 que cumplen
que cumplen
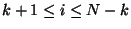 , ya que para
las partículas de los extremos de la cadena, no existen
exactamente sus
, ya que para
las partículas de los extremos de la cadena, no existen
exactamente sus 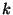 vecinos, entonces para eliminar la
restricción del índice, en otras palabras, establecer una
ecuación que sea válida para toda partícula de la cadena,
se supone que existen
vecinos, entonces para eliminar la
restricción del índice, en otras palabras, establecer una
ecuación que sea válida para toda partícula de la cadena,
se supone que existen 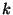 partículas ficticias a cada lado de
la red, con desplazamientos
partículas ficticias a cada lado de
la red, con desplazamientos 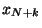 ,
,
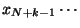 ,
,
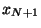 y
y 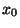 ,
, 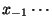 ,
, 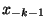 , cuyos valores
se postulan idénticamente cero.
En forma matricial las Ecs. (I.1) son
, cuyos valores
se postulan idénticamente cero.
En forma matricial las Ecs. (I.1) son
![\begin{displaymath}
\left[ \begin{array}{c}
m_{1} \ddot{x}_{1} \\
m_{2} \dd...
..._{k} \\
\\
\vdots \\
\\
x_{N}
\end{array} \right]
\end{displaymath}](img20.png) |
(I.2) |
se observa que la matriz de las constantes elásticas,
tiene elementos distintos de cero, únicamente en una banda de
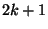 diagonales, la diagonal principal está en el centro de la
banda.
Si definimos a
diagonales, la diagonal principal está en el centro de la
banda.
Si definimos a 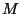 como la siguiente matriz diagonal
como la siguiente matriz diagonal
a 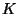 como la matriz de las
como la matriz de las 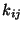 y a
y a 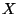 como el
vector columna de los desplazamientos de cada una de las
partículas, en forma concisa la ecuación (I.2) queda
como el
vector columna de los desplazamientos de cada una de las
partículas, en forma concisa la ecuación (I.2) queda
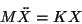 |
(I.3) |
Desde el punto de vista algebraico, el método más simple para
obtener la solución de la ecuación anterior, es multiplicar
por 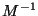 , con lo que se tiene
, con lo que se tiene
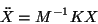 |
(I.4) |
Si suponemos que 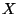 es un eigenvector de la matriz
es un eigenvector de la matriz 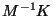 ,
se obtiene
,
se obtiene
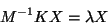 |
(I.5) |
o también
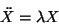 |
(I.6) |
que se reconoce como una ecuación diferencial para los
modos normales de movimiento, las soluciones en términos de
exponenciales complejas se conocen muy bien, pero la
inconveniencia primordial del proceso anterior es que, la matriz
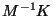 no es simétrica cuando las masas de las
partículas son distintas, que implica que los cálculos
numéricos sean más laboriosos, aún cuando la derivación
algebraica se simplifique.
El obstáculo anterior se elimina si definimos
no es simétrica cuando las masas de las
partículas son distintas, que implica que los cálculos
numéricos sean más laboriosos, aún cuando la derivación
algebraica se simplifique.
El obstáculo anterior se elimina si definimos
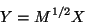 |
(I.7) |
ya que entonces la ecuación (I.3) se puede escribir de la
siguiente manera
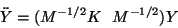 |
(I.8) |
en donde ahora
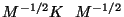 es una matriz simétrica, y gracias a
ello es posible trabajar con sus eigenvalores y eigenvectores que
van a ser ortogonales, los elementos de dicha matriz son de la
forma
es una matriz simétrica, y gracias a
ello es posible trabajar con sus eigenvalores y eigenvectores que
van a ser ortogonales, los elementos de dicha matriz son de la
forma
De cualquier manera, la matriz que necesita ser diagonalizada es
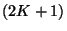 diagonal, que permite emplear una técnica recursiva
para obtener sus eigenvalores y eigenvectores. Para evitar
confusión denotemos por
diagonal, que permite emplear una técnica recursiva
para obtener sus eigenvalores y eigenvectores. Para evitar
confusión denotemos por 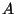 a la matriz
a la matriz 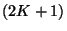 diagonal, sin
tener en cuenta si es
diagonal, sin
tener en cuenta si es 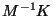 ó
ó 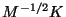
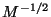 y examinemos
su ecuación de eigenvalores, que es a lo que tenemos que avocarnos
y examinemos
su ecuación de eigenvalores, que es a lo que tenemos que avocarnos
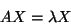 |
(I.9) |




Next: Matriz de transferencia
Up: Breve análisis de vibraciones
Previous: Breve análisis de vibraciones
Contents
Pedro Hernandez
2006-02-20
![\includegraphics[width=5in]{f01p04.eps}](img4.png)
![\includegraphics[width=5in]{f01p04.eps}](img4.png)
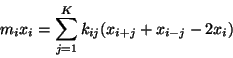
![\begin{displaymath}
\left[ \begin{array}{c}
m_{1} \ddot{x}_{1} \\
m_{2} \dd...
..._{k} \\
\\
\vdots \\
\\
x_{N}
\end{array} \right]
\end{displaymath}](img20.png)
![\begin{displaymath}
M = \left[ \begin{array}{cccc}
m_1 & 0 & \dots & 0 \\
0 ...
... \cdot & \cdot \\
0 & \cdots & & m_{N}
\end{array} \right]
\end{displaymath}](img23.png)