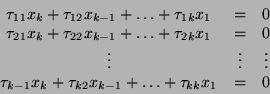


Next: Interpretación de los eigenvalores
Up: Breve análisis de vibraciones
Previous: Matriz de movimiento
Contents
Si se escribe la ecuación anterior en términos de las componentes
de 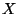 , se tiene
, se tiene
 |
(I.10) |
para toda
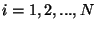 ; ya que, como dijimos al
principio
; ya que, como dijimos al
principio
de (I.10) es posible escribir
donde
y
Se ve que las ecuaciones (I.11b) tienen la forma de una
relación de diferencia finita, que definen a 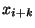 en
términos de los desplazamientos de sus
en
términos de los desplazamientos de sus  partículas
antecesoras.
De las muchas técnicas, para obtener la solución
de sistemas lineas de ecuaciones de diferencia finita, una de las
más adecuadas es establecer el sistema en forma matricial.
Entonces si se añaden a las ecuaciones (I.11b) las
partículas
antecesoras.
De las muchas técnicas, para obtener la solución
de sistemas lineas de ecuaciones de diferencia finita, una de las
más adecuadas es establecer el sistema en forma matricial.
Entonces si se añaden a las ecuaciones (I.11b) las 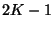 identidades triviales.
identidades triviales.
producen un sistema que se escribe como
![\begin{displaymath}
\left [ \begin{array}{c}
x_{i + k} \\
x_{i + k - 1} \\ ...
...
x_{i + k -2} \\
\vdots \\
x_{i - k}
\end{array} \right]
\end{displaymath}](img53.png) |
(I.12) |
o de una manera más concisa
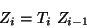 |
(I.13) |
A la matriz  de coeficientes es a la que se le denomina
Matriz de Transferencia, debido a que mediante su uso podemos conocer el
desplazamiento de la partícula
de coeficientes es a la que se le denomina
Matriz de Transferencia, debido a que mediante su uso podemos conocer el
desplazamiento de la partícula  , si se conocen los desplazamientos
de sus
, si se conocen los desplazamientos
de sus  partículas antecesoras, y es posible
efectuarlo desde la partícula
partículas antecesoras, y es posible
efectuarlo desde la partícula 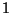 hasta la
hasta la 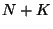 , que es en realidad en lo que estamos
interesados. Así se tiene
, que es en realidad en lo que estamos
interesados. Así se tiene
si se efectua la cadena de sustituciones, se tiene
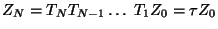 |
|
|
(I.14) |
donde 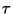 denota al producto de las
denota al producto de las 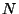 matrices de
transferencia que para una cadena arbitraria todas ellas son
distintas, el producto es en el orden correspondiente a la
sucesión de partículas de que está compuesta la cadena.
Para una cadena uniforme, es decir, en la que todas las masas constantes
de resorte son las mismas, se tiene una simplificación ya que todas las
matrices de
transferencia que para una cadena arbitraria todas ellas son
distintas, el producto es en el orden correspondiente a la
sucesión de partículas de que está compuesta la cadena.
Para una cadena uniforme, es decir, en la que todas las masas constantes
de resorte son las mismas, se tiene una simplificación ya que todas las
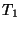 son iguales y por lo tanto
son iguales y por lo tanto
 |
(I.15) |
Es claro, que los elementos de 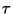 son polinomios en
son polinomios en
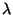 , ya que cada
, ya que cada  depende en
depende en 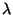 .
Donde los vectores
.
Donde los vectores 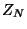 y
y 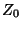 escritos explícitamente
son:
escritos explícitamente
son:
ahora bien, si hacemos uso de las condiciones
suplementarias (I.11a), éstos toman la siguiente forma
De la ecuación (I.14) podemos escribir el siguiente sistema
homogéneo de ecuaciones lineales
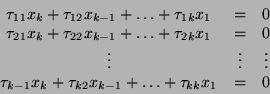 |
(I.16) |
donde cada
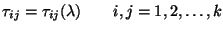 Sabemos que existirá una solución no trivial para las
Sabemos que existirá una solución no trivial para las
 si y sólo si se cumple lo
siguiente
si y sólo si se cumple lo
siguiente
 |
(I.17) |
que es otra forma de establecer la ecuación
característica para 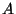 que era de esperarse, ya que las
condiciones suplementarias, no son otra cosa que un tipo de
condiciones a las frontera.
Es claro que los desplazamientos iniciales
que era de esperarse, ya que las
condiciones suplementarias, no son otra cosa que un tipo de
condiciones a las frontera.
Es claro que los desplazamientos iniciales
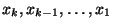 forman un eigenvector de la submatriz de
forman un eigenvector de la submatriz de 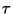 perteneciente al
eigenvalor cero.
perteneciente al
eigenvalor cero.



Next: Interpretación de los eigenvalores
Up: Breve análisis de vibraciones
Previous: Matriz de movimiento
Contents
Pedro Hernandez
2006-02-20



![\begin{displaymath}
\left [ \begin{array}{c}
x_{i + k} \\
x_{i + k - 1} \\ ...
...
x_{i + k -2} \\
\vdots \\
x_{i - k}
\end{array} \right]
\end{displaymath}](img53.png)
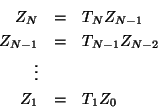
![\begin{displaymath}
Z_{N} = \left[ \begin{array}{cccc}
x_{N + k} \\
x_{N + k...
...
x_{N} \\
\vdots \\
x_{N - k + 1}
\end{array} \right]
\end{displaymath}](img66.png)
![\begin{displaymath}
Z_{0} = \left[ \begin{array}{cccc}
x_{k} \\
x_{k - 1} \\...
...} \\
x_{0} \\
\vdots \\
x_{-k + 1}
\end{array} \right]
\end{displaymath}](img67.png)
![\begin{displaymath}
Z_{N} = \left[ \begin{array}{cccc}
0 \\
0 \\
\vdots \\...
...\
x_{N} \\
\vdots \\
x_{N - k + 1}
\end{array} \right]
\end{displaymath}](img68.png)
![\begin{displaymath}
Z_{0} = \left[ \begin{array}{cccc}
x_{k} \\
x_{k - 1} \\...
...ots \\
x_{1} \\
0 \\
\vdots \\
0
\end{array} \right]
\end{displaymath}](img69.png)