Next: Referencias
Up: Diversos aspectos de la
Previous: Condición para obtener los
Contents
Hemos visto en este Capítulo que es posible representar a
las Matrices de Transferencia en varias formas, una que es
análoga a la fórmula de Euler para números complejos y que
está dada por la Ec. (IV.10'), otra denominada vectorial en
donde los ``vectores" bases son las Matrices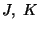 
y 
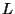dada
por (IV.10) y finalmente en la que cada Matriz de Transferencia
representa un arco sobre la superficie de un hiperboloide de una
sóla rama. En las dos últimas representaciones se obtuvieron
las analogías con respecto a la multiplicación de las
matrices directamente, que en una consiste en una suma vectorial,
y en la otra también en una suma pero de arcos sobre el
hiperboloide.
También se obtuvo una parametrización de las ``rotaciones''
que representan los arcos del hiperboloide, en el producto de dos
Involuciones.
Finalmente se obtuvo en la representación vectorial la
condición para la existencia de las frecuencias naturales de la
red unidimensional.
// FOR
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
SUBROUTINE TRIEV ( Z,K )
C
C APENDICE A
C
C TRIEV (Z,K) EVALUA LAS COMPONENTES DEL EIGENVECTOR K ,
C CUYO EIGENVENVALOR ES V(K). SIEMPRE SE TOMA LA PRIMERA
C COMPONENTE IGUAL A 1.0, Y LAS DEMAS SE CALCULAN RECURSI-
C VAMENTE MEDIANTE LAS MATRICES Q. EN EL ARREGLO Z SE AL-
C MACENA EL EIGENVECTOR DESEADO.
DIMENSION S(31),T(32)
DIMENSION Z(31)
COMMON N,LI,LO,LP,LT,IC,X0,XN
COMMON V(31),Q(2,2)
COMMON A(30),B(30),C(30)
EQUIVALENCE (S(1),T(2))
T(1)=0.0
T(2)=1.0
DO 10 J=1,N
10 S(J+1)=(A(J)+V(K)*C(J))*T(J+1)+B(J)*T(J)
N1=N+1
DO 30 I=1,N1
30 Z(I)=S(I)
RETURN
END
// FOR
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
SUBROUTINE TRIGE
C TRIGE GRAFICA POR IMPRESORA LA COLECCION COMPLETA DE
C EIGENVECTORES, USANDO INFORMACION QUE PREVIAMENTE SE
C ALMACENO EN EL DISCO.
DIMENSION Z(31)
COMMON N,LI,LO,LP,LT,IC,X0,XN
COMMON V(31),Q(2,2)
COMMON B(30),A(30),C(30)
DO 32 I=1,N
CALL TRIPG (Z,N,0,10,1)
CALL TRIPG (Z,N,0,10,2)
DO 31 J=1,41
CALL TRIST (Z,N,100+I,J,5)
30 CALL TRIST (Z,N,J,10,3)
32 CALL TRIPG (Z,N,0,10,5)
RETURN
END
// FOR
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
SUBROUTINE TRIGR (Z,W)
C TRIGR (Z,W) FORMA LA GRAFICA DE LAS FRECUENCIAS, LO
C HACE EN 120 COLUMNAS, EN EL ARREGLO Z ESTAN ALMACENADAS
C LAS FRECUENCIAS Y W ES UN FACTOR DE ESCALA.
DIMENSION Z(1)
DIMENSION III(120)
COMMON N,LI,LO
DO 11 I=1,120
11 III(I)=16448
DO 12 I=1,120,20
12 III(I)=-14016
S=120.0/W
DO 27 I=1,N
L=IFIX(-Z(I)*S)+1
IF (L) 27,27,21
21 IF (L-120) 22,22,27
22 III(L)=23616
27 CONTINUE
WRITE (LC,300) III
300 FORMAT (1X,120A1)
RETURN
END
// FOR
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
SUBROUTINE TRIII
C TRIII CALCULA LOS LIMITES DE GERSCHGORIN DE LOS EIGEN-
C VALORES Y FORMA LOS COEFICIENTES USADOS EN LAS RELACIO-
C NES RECURSIVAS COMO ELEMENTOS DE LAS Q'S.
COMMON N,LI,LO,LP,LT,IC,I0,X0,XN
COMMON V(31),Q(2,2)
COMMON B(30),A(30),C(30)
C ESTABLECE LOS LIMITES DE GERSCHGORIN PARA LOS EIGENVA-
C LORES.
R=ABS(C(1))
X0=B(1)-R
XN=B(1)+R
IF (N-2) 30,15,10
10 N1=N-1
DO 14 I=2,N1
R = ABS(A(I))+ABS(C(I))
IF (X0-(B(I)-R)) 12,12,11
11 X0=B(I)-R
12 IF (XN-(B(I)+R)) 13,14,14
13 XN=B(I)+R
14 CONTINUE
15 R=ABS(A(N))
IF (X0-(B(N)-R)) 17,17,16
16 X0=B(N)-R
17 IF (XN-(B(N)+R)) 18,19,19
18 XN=B(N)+R
19 CONTINUE
C FORMA LOS COEFICIENTES USADOS EN LAS RELACIONES RECUR-
C SIVAS.
DO 20 I=1,N
R=1.0/C(I)
A(I)=-A(I)*R
B(I)=-B(I)*R
20 C(I)=R
30 RETURN
END
// FOR
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
SUBROUTINE TRINO (Z,N)
C TRINO (N,Z) NORMALIZA LAS N PRIMERAS COMPONENTES DEL
C VECTOR Z.
DIMENSION Z(1)
A=0.0
DO 5 I=1,N
5 A=A+Z(I)**2
A=1.0/SQRT(A)
DO 7 I=1,N
7 Z(I)=A*Z(I)
RETURN
END
// FOR
*LIST WORD INTEGERS
*EXTENDED PRECISION
SUBROUTINE TRIPG (Z,N,M,K,L)
C TRIPG ((Z,N,M,K,L) HACE UNA GRAFICA DE UNA PAGINA PARA
C CADA EIGENVECTOR. Z ES EL VECTOR QUE CONTIENE LAS COM-
C PONENTES DEL EIGENVECTOR, N ES SU DIMENSION, M ES EL NU-
C MERO DE VARIACIONES DESEADAS, EN REALIDAD UNA TERCERA
C COORDENADA, K ES EL NUMERO DE ARCHIVO Y L ES LA OPCION
C DESEADA.
C L=1 GENERA LA IMAGEN DE UNA PAGINA EN BLANCO SOBRE
C EL DISCO.
C L=2 GENERA LINEAS DE EQUILIBRIO.
C L=3 COLOCA LAS COMPONENTES DEL EIGENVECTOR ADECUADA-
C MENTE
C L=5 IMPRIME LA PAGINA DE GRAFICA TERMINADA
DIMENSION Z(1),JJJ(120)
COMMON N8,LI,LO,LP
GO TO (10,20,30,40,50),L
10 CONTINUE
DO 11 I=1,120
11 JJJ(I)=16448
DO 12 I=1,57
12 WRITE(K'I) JJJ
RETURN
20 CONTINUE
DO 21 I=1,N
DO 21 J=1,41
21 CALL TRIPL (5*I+J,50-J,10,19264)
RETURN
30 CONTINUE
DO 31 I=1,N
31 CALL TRIPL (5*I+M,50-(IFIX(10.0*Z(I))+M),10,23616)
RETURN
40 CONTINUE
WRITE (K'M) (Z(J),J=1,N)
RETURN
50 CONTINUE
WRITE (LO,352)
WRITE (LO,350)
DO 51 I=1,57
READ (K'I) JJJ
WRITE (LO,351) JJJ
51 CONTINUE
WRITE (LO,350)
RETURN
350 FORMAT (1X,12('ESFM*1970*'))
351 FORMAT (1X,120A1)
352 FORMAT (1H1)
END
// FOR
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
SUBROUTINE TRIPL (IA,IB,K,ICH)
C TRIPL (IA,IB,K,ICH) INTRODUCE EL CARACTER ICH EN EL
C ARCHIVO DEL DISCO K, EN LA COLUMNA IA DEL REGISTRO IB.
DIMENSION III(120)
IF (IA) 1,1,2
1 IA=1
2 IF (120-IA) 3,3,4
3 IA=120
4 IF (IB) 5,5,6
5 IB=1
6 IF (57-IB) 7,7,8
7 IB=57
8 READ (K'IB) III
III(IA)=ICH
WRITE (K'IB) III
RETURN
END
// FOR
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
SUBROUTINE TRIQK (X,Y,K)
C DO K EN EL PUNTO X, DEPOSITA EL VALOR EN Y. EN EL PROCESO
C TRIQK (X,Y,K) EVALUA EL POLINOMIO CARACTERISTICO DE GRASO
C LA MATRIZ Q, DE LA QUE SE DESEA EL VALOR DEL ELEMENTO (1,1).
C SOLO SE EVALUA LA PRIMERA COLUMNA DE Q YA QUE NO ES NECESARIA
C LA SEGUNDA.
COMMON N,LI,L0,LP,LT,I0,X0,XN
COMMON V(31),Q(2,2)
COMMON A(30),B(30),C(30)
EQUIVALENCE (Q11,Q(1,1)),(Q21,Q(2,1))
RS(X,Y) =SIGN(1.0,X)-SIGN(1.0,Y)
I0=0
Y0=1.0
Q11=1.0
Q21=0.0
IF (K-1) 30,10,10
10 D0 20 J=1,K
W1=(A(J)+X*C(J))*Q11+B(J)*Q21
Q21=Q11
Q11=W1
IF (RS(Q11,Y0)) 15,20,15
15 I0=I0+1
Y0=-Y0
20 CONTINUE
30 Y=Q11
RETURN
END
// FOR
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
SUBROUTINE TRIRK (Z,K)
C TRIRK (Z,K) LOCALIZA LA RAIZ K DEL POLINOMIO CARACTERIS-
C TICO QK, QUE SE DEPOSITA EN Z. LA PRIMERA RAIZ ES LA
C MAS NEGATIVA MIENTRAS QUE LA ULTIMA ES LA MAS POSITIVA.
DIMENSION XX(2),KK(2)
COMMON N,LI,LO,LP,LT,I0,X0,XN
COMMON V(31),Q(2,2)
COMMON B(30),A(30),C(30)
EQUIVALENCE (X1,XX(1)),(X2,XX(2))
KK(1)=K-1
KK(2)=K
X1=X0
X2=XN
DO 15 I=1,2
10 X=0.5*(X1+X2)
CALL TRIQK (X,Y,K)
IF (I0-KK(I)) 11,15,12
11 X1=X
GO TO 10
12 X2=X
GO TO 10
15 XX(I)=X
CALL TRIZR (X1,X2,Z,K)
RETURN
END
// FOR
*LIST SOURCE PROGRAM
* ONE WORD INTEGERS
* EXTENDED PRECISION
SUBROUTINE TRIRO
C TRIRO LOCALIZA LAS RAICES DEL POLINOMIO CARACTERISTICO
C POR UN PROCESO RECURSIVO QUE USA LAS RAICES DE LAS SUB-
C MATRICES PARA AISLAR LAS DE LA MATRIZ ORIGINAL. SE UTI-
C LIZA EL METODO DE 'REGULA FALSI' COMBINADO CON EL DE
C AITKEN DEL CUADRADO DE LA DELTA.
DIMENSION T(31),U(32)
COMMON N,LI,LO,LP,LT,I0,X0,XN
COMMON V(31),Q(2,2)
COMMON A(30),B(30),C(30)
RS(X,Y) = SIGN(1.0,X)-SIGN(1.0,Y)
U(1)=X0
V(1)=-A(1)/C(1)
C LOS CEROS DE POLINOMIO ANTERIOR DETERMINAN LOS INTERVA-
C LOS PARA ESTE CICLO, ASI COMO TAMBIEN EL FACTOR DE ESCA-
C LA QUE SERA EMPLEADO.
DO 500 K=2,N
CALL TRIQK(X0,T(1),K)
DO 10 I=2,K
U(I)=V(I-1)
CALL TRIQK (U(I),T(I),K)
10 CONTINUE
U(K+1)=XN
CALL TRIQK (XN,T(K+1),K)
U(K+2)=XN+0.01
DO 20 I=1,K
IF (RS(T(I),T(I+1))) 20,12,20
12 XX=U(I+1)+1.0E-3*ABS(U(I+2)-U(I))
CALL TRIQK (XX,YY,K)
IF(RS(T(I),YY)) 13,14,13
13 U(I+1)=XX
T(I+1)=YY
GO TO 20
14 XX=U(I+1)-1.0E-3*ABS(U(I+1)-U(I))
CALL TRIQK (XX,YY,K)
IF (RS(T(I),YY)) 13,15,13
15 WRITE (LO,3000)
3000 FORMAT (1X,'BAD INTERVAL')
20 CONTINUE
C UNA RAIZ SE DEBE LOCALIZAR PARA CADA UNO DE LOS K INTER-
C VALOS.
DO 400 I=1,K
CALL TRIZR (U(I),U(I+1),V(I),K)
400 CONTINUE
500 CONTINUE
RETURN
END
// FOR
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDER PRECISION
SUBROUTINE TRIST (Z,N,K,M,L)
C TRIST (Z,N,K,M,L) ALMACENA Y RECUPERA LOS VECTORES DEL
C DISCO DE ACUERDO CON LA OPCION L. EL ARGUMENTO ES UN
C VECTOR Z DE DIMENSION N.K ES EL ARCHIVO QUE SE UTILIZA-
C RA Y M EL REGISTRO.
C L=1 IMPRIME LETRERO POR CONSOLA PARA EL OPERADOR.
C L=2 PERFORA LAS COMPONENTES DE Z.
C L=3 LEE TARJETAS QUE CONTIENEN LAS COMPONENTES
C DE LOS VECTORES.
C L=4 PRUEBA PARA CONTINUIDAD DE LOS VECTORES.
C L=5 BUSCA EL VECTOR EN EL DISCO Y LO PASA A MEMO-
C RIA.
C L=6 ALMACENA EL VECTOR EN EL DISCO.
DIMENSION X(31),Y(31),Z(31)
COMMON N8,LI,LO,LP
GO TO (10,20,30,40,50,60),L
10 CONTINUE
WRITE (1,100)
100 FORMAT (' CLEAR CARDS FROM THE CARD READER AND INSERT BLANK CARDS'
* ///)
PAUSE
RETURN
20 CONTINUE
WRITE (LP,200) (Z(I),I=1,N)
RETURN
30 CONTINUE
READ (LI,200) (Z(I),I=1,N)
200 FORMAT (8F10.6)
RETURN
40 CONTINUE
READ (K'M) X
DO 46 J=2,M
READ (K'J) Y
A=0.0
B=0.0
DO 41 I=1,N
A=A+ABS(Y(I)-X(I))
B=B+ABS(Y(I)+X(I))
41 CONTINUE
IF (A-B) 44,44,42
42 DO 43 I=1,N
43 Y(I)=-Y(I)
44 DO 45 I=1,N
45 X(I)=Y(I)
46 WRITE (K'J) Y
RETURN
50 CONTINUE
READ (K'M) (Z(I),I=1,N)
RETURN
60 CONTINUE
WRITE (K'M) (Z(I),I=1,N)
RETURN
END
// FOR
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
SUBROUTINE TRIZR (AA,BB,U,K)
C TRIZR (AA,BB,U,K) CALCULA LA RAIZ DE QK QUE SE HALLA
C EN EL INTERVALO (AA,BB), DEPOSITA LA LOCALIZACION EN U.
C SE UTILIZA UNA COMBINACION DE 'REGULA FALSI', BISECCION
C Y EL PROCESO DE AITKEN DEL CUADRADO DE LA DELTA.
DIMENSION J(2),R(2)
COMMON N,LI,LO,LP,LT,I0,X0,XN
COMMON V(31),Q(2,2)
COMMON A(30),B(30),C(30)
EQUIVALENCE (J1,J(1)),(J2,J(2)),R1,R(1)),(R2,R(2))
SIZ(X) =ABS(X)-EPS
WID(X,Y) =ABS(Y-X)-DEL
RS(X,Y) =SIGN(1.0,X)-SIGN(1.0,Y)
X1=AA
CALL TRIQK (X1,Y1,K)
X2=BB
CALL TRIQK (X2,Y2,K)
DEL=0.1E-6*ABS(X2-X1)
C AUNQUE LOS EXTREMOS DEL INTERVALO NO PUEDEN SER RAICES
C DEL POLINOMIO, LA EXPERIENCIA HA MOSTRADO QUE PUEDEN
C ESTAR DEMASIADO PROXIMOS A LOS CEROS PARA REPRESENTAR
C LA ESCALA DEL POLINOMIO EXACTAMENTE. POR LO QUE SE USAN
C DOS VALORES INTERIORES, COMO SE SABE AL MENOS HAY UNA
C RAIZ EN EL INTERIOR DE CADA INTERVALO.
A1=(X1+X1+X2)/3.0
A2=(X1+X2+X2)/3.0
CALL TRIQK (A1,Z1,K)
CALL TRIQK (A2,Z2,K)
IF (RS(Z1,Z2)) 21,22,21
21 X1,A1
Y1=Z1
X2=A2
Y2=Z2
GO TO 25
22 IF (RS(Y1,Z1)) 23,24,23
23 X2=A1
Y2=Z1
GO TO 25
24 X1=A2
Y1=Z2
25 CONTINUE
EPS=0.5E-9*(ABS(Z1)+ABS(Z2))
C EMPLEANDO EL METODO DE 'REGULA FALSI' NORMALMENTE SE
C ENCUENTRA QUE EL VALOR DE LA FUNCION EN UN EXTREMOS ES
C MUCHO MENOR QUE EN EL OTRO, CUANDO ES MUY PEQUENO, EL
C PUNTO SE PUEDE TOMAR COMO UNA RAIZ, CUANDO LA RAZON
C DE LOS EXTREMOS ES MENOR QUE LA PRECISION DE LA COMPU-
C TADORA, LA NUEVA APROXIMACION SERA DESCONFIABLE,
C ENTONCES EL EXTREMO, MAYOR DEBE SER TRASLADADO.
DO 200 M=1,30
X=0.5*(X1,X2)
CALL TRIQK (X,Y,K)
IF (RS(Y,Y1)) 106,105,106
105 X1=X
Y1=Y
GO TO 107
106 X2=X
Y2=Y
107 IF (WID(X1,X2)) 108,108,110
108 U=0.5*(X1+X2)
RETURN
110 IF (ABS(Y1/Y2+Y2/Y1)-1.0E-6) 125,200,200
125 CONTINUE
S1=X1
S2=X2
C DOS CICLOS DE 'REGULA FALSI'
DO 135 L=1,2
R(L)=(X1*Y2-Y2*Y1)/(Y2-Y1)
CALL TRIQK (R(L),Y,K)
IF (SIZ(Y)) 131,131,132
131 U=R(L)
RETURN
132 IF (RS(Y,Y1)) 134,133,134
133 X1=R(L)
Y1=Y
J(L)=-1
GO TO 135
134 X2=R(L)
Y2=Y
J(L)=1
135 CONTINUE
C EL PROCESO DE AITKEN DEL CUADRADO DE LA DELTA PROPOR-
C CIONA LAS ULTIMAS DOS APROXIMACIONES TRASLADADAS AL
C MISMO PUNTO EXTREMO, Y PROPORCIONA LA NUEVA ESTIMACION
C LOCALIZADA DENTRO DEL INTERVALO.
IF (J1+J2) 141,200,142
141 R0=S1
GO TO 150
142 R0=S2
150 X=(R0*R2-R1*R1)/(R0-R1-R1+R2)
IF (X1-X) 151,200,200
151 IF (X-X2) 152,200,200
152 CALL TRIQK (X,Y,K)
IF (SIZ(Y)) 153,153,154
153 U=X
RETURN
154 IF (RS(Y,Y1)) 156,155,156
155 X1=X
Y1=Y
GO TO 200
156 X2=X
Y2=Y
200 CONTINUE
RETURN
END
// FOR
*I00S(2501 READER,1403 PRINTER,DISK)
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
*NAME TRIIR
C
C APENDICE B
C
C TRIIR ES EL PROGRAMA PRINCIPAL QUE JUNTO CON LAS
C SUBRUTINAS TRILE Y TRIGM DIBUJA EN PERSPECTIVA POR
C GRAFICADOR LOS MODOS NORMALES DE VIBRACION, HACE USO
C DE LA INFORMACION PREVIAMENTE ALMACENADA EN EL DISCO.
DIMENSION Z(31),X(31)
DIMENSION U(41),V(41)
DEFINE FILE 10(41,93,U,K0)
DEFINE FILE 101(41,93,U,K01)
DEFINE FILE 102(41,93,U,K02)
DEFINE FILE 103(41,93,U,K03)
DEFINE FILE 104(41,93,U,K04)
DEFINE FILE 105(41,93,U,K05)
DEFINE FILE 106(41,93,U,K06)
DEFINE FILE 107(41,93,U,K07)
DEFINE FILE 108(41,93,U,K08)
DEFINE FILE 109(41,93,U,K09)
DEFINE FILE 110(41,93,U,K10)
DEFINE FILE 111(41,93,U,K11)
DEFINE FILE 112(41,93,U,K12)
DEFINE FILE 113(41,93,U,K13)
DEFINE FILE 114(41,93,U,K14)
DEFINE FILE 115(41,93,U,K15)
DEFINE FILE 116(41,93,U,K16)
DEFINE FILE 117(41,93,U,K17)
DEFINE FILE 118(41,93,U,K18)
DEFINE FILE 119(41,93,U,K19)
DEFINE FILE 120(41,93,U,K20)
LI=8
READ (LI,100) N,M
100 FORMAT (2I2)
CALL SCALE (0.2,1.2,-60.0,-0.2)
NM=1
N2=N/2
DO 50 K2=1,N2
DO 50 K1=1,2
L=1
DO 12 I=1,M
KK=100+(K1-1)*N2+K2
READ (KK'I) Z
DO 13 J=1,N
Z(J)=-10.0*Z(J)-I
13 X(J)=J+0.1*I
CALL TRIGM (Z,X,N,L)
12 CONTINUE
CALL EPLOT (1,0.0,0.0)
L=1
DO 16 J=1,N
DO 15 I=1,M
U(I)=-I
15 V(I)=J+0.1*I
CALL TRILE(U,V,M,L)
16 CONTINUE
CALL EPLOT (1,0.0,0.0)
GO TO (30,31),NM
30 CALL SCALE (0.2,1.2,0.0,-10.0)
NM=2
GO TO 50
31 CALL SCALE (0.2,1.2,-70.0,10.0)
NM=1
GO TO 50
50 CONTINUE
CALL EXIT
END
// FOR
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
SUBROUTINE TRIGM (X,Z,N,L)
C TRIGM (X,Z,N,L) DIBUJA LAS COMPONENTES DE LOS MODOS
C NORMALES. X ES LA COORDENADA DEL NUMERO DE PARTICULAS,
C Z ES LA AMPLITUD DE VIBRACION, N ES LA LONGITUD DE LA
C CADENA Y L ES UNA OPCION
C L=1 DIBUJA HACIA LA IZQUIERDA
C L=2 DIBUJA HACIA LA DERECHA
DIMENSION Z(31),X(31)
GO TO (1,2),L
1 DO 10 I=1,N
CALL EPLOT (-2,X(I),Z(I))
10 CALL POINT (1)
CALL EPLOT (1,X(N),Z(N))
L=2
RETURN
2 DO 12 I=1,N
J=N-I+1
CALL EPLOT (-2,X(J),Z(J))
12 CALL POINT (1)
CALL EPLOT (1,X(1),Z(1))
L=1
RETURN
END
// FOR
*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
SUBROUTINE TRILE(U,V,N,L)
C TRILE (U,V,N,L) DIBUJA LAS POSICIONES DE EQUILIBRIO DE
C LAS PARTICULAS, U Y V SON LAS COORDENADAS, N ES LA DI-
C MENSION DE LA CADENA Y L ES UNA OPCION PARA QUE LA PLU-
C MA DEL GRAFICADOR VAYA EN UNA DIRECCION
C L=1 HACIA ABAJO.
C L=2 HACIA ARRIBA.
DIMENSION U(41),V(41)
GO TO (1,2),L
1 DO 10 I=1,N
10 CALL EPLOT(-2,U(I),V(I))
CALL EPLOT(1,U(N),V(N))
L=2
RETURN
2 DO 12 I=1,N
J=N-I+1
12 CALL EPLOT(-2,U(J),V(J))
CALL EPLOT(1,U(1),V(1))
L=1
RETURN
END
// FOR
*IOOS(2501 READER,1403 PRINTER,DISK)
*LIST ALL
*ONE WORD INTEGERS
*EXTENDED PRECISION
*NAME TRIVM
C
C APENDICE C
C
C TRIVM ES UN PROGRAMA PRINCIPAL QUE VARIA SISTEMATICA-
C MENTE LA MASA DE LA PARTICULA K DE UNA CADENA UNIFORME.
C SE CALCULAN E IMPRIMEN LOS EIGENVALORES Y EIGENVECTORES
C PARA CADA INCREMENTO EN LA MASA PERTURBADA.
DIMENSION Z(31)
COMMON N.LI,LO,LP,LT,I0,X0,XN
COMMON V(31),Q(2,2)
COMMON B(30),A(30),C(30)
DEFINE FILE 10(57,120,U,K00)
DEFINE FILE 101(41,93,U,K01)
DEFINE FILE 102(41,93,U,K02)
DEFINE FILE 103(41,93,U,K03)
DEFINE FILE 104(41,93,U,K04)
DEFINE FILE 105(41,93,U,K05)
DEFINE FILE 106(41,93,U,K06)
DEFINE FILE 107(41,93,U,K07)
DEFINE FILE 108(41,93,U,K08)
DEFINE FILE 109(41,93,U,K09)
DEFINE FILE 110(41,93,U,K10)
DEFINE FILE 111(41,93,U,K11)
DEFINE FILE 112(41,93,U,K12)
DEFINE FILE 113(41,93,U,K13)
DEFINE FILE 114(41,93,U,K14)
DEFINE FILE 115(41,93,U,K15)
DEFINE FILE 116(41,93,U,K16)
DEFINE FILE 117(41,93,U,K17)
DEFINE FILE 118(41,93,U,K18)
DEFINE FILE 119(41,93,U,K19)
DEFINE FILE 120(41,93,U,K20)
LI=8
LO=5
LP=9
F=EXP(ALOG(16.0)/40.0)
1 READ (LI,2000) N,K
2000 FORMAT (2I2)
IF (N) 2,2,3
2 WRITE (LO,3000)
3000 FORMAT (59X,'FIN')
CALL EXIT
3 CONTINUE
X=0.25
DO 20 M=1,41
DO 10 J=1,N
A(J)=1.0
B(J)=-2.0
10 C(J)=1.0
UU=1.0/X
Y=SQRT(UU)
C(K-1)=Y
A(K)=Y
B(K)=-2.0*UU
C(K)=Y
A(K+1)=Y
CALL TRIII
CALL TRIRO
CALL TRIGR (V,6.0)
D0 12 I=1,N
CALL TRIEV (Z,I)
Z(K)=Y*Z(K)
CALL TRINO (Z,N)
12 CALL TRIST (Z,N,100+I,M,6)
20 X=X*F
WRITE (LO,400) N,K
400 FORMAT(' GRAFICA DEL NEGATIVO DEL CUADRADO DE LAS FRE'
1'CUENCIAS NATURALES DE UNA CADENA HOMOGENEA'/' DE',I2,
2' PARTICULAS, EN LA QUE SE MODIFICA SISTEMATICAMENTE LA'
3' MASA DE LA PARTICULA',I2,','/' DONDE EL EJE Y CORRES'
4' PONDE A DICHO PARAMETRO.')
DO 32 I=1,N
CALL TRIPG (Z,N,0,10,1)
CALL TRIPG (Z,N,0,10,2)
DO 31 J=1,41
CALL TRIST (Z,N,100+I,J,5)
31 CALL TRIPG (Z,N,J,10,3)
32 CALL TRIPG (Z,N,0,10,5)
GO TO 1
END
// FOR
*IO0S(2501 READER,1403 PRINTER,DISK)
189'*LIST SOURCE PROGRAM
*ONE WORD INTEGERS
*EXTENDED PRECISION
*NAME TRIVK
C
C APENDICE D
C
C TRIVK ES UN PROGRMA PRINCIPAL QUE VARIA SISTEMATICA-
C MENTE LA CONSTANTE ELASTICA ENTRE LAS PARTICULAS K Y
C K+1 EN UNA CADENA HOMOGENEA HACIENDO USO DE LAS SUB-
C RUTINAS PARA MATRICES TRIDIAGONALES CALCULA E IMPRIME
C LOS EIGENVALORES Y EIGENVECTORES PARA CADA INCREMENTO
C EN LA CONSTANTE ELASTICA.
DIMENSION Z(31)
COMMON N,LI,LO,LP,LT,I0,X0,XN
COMMON V(31),Q(2,2)
COMMON B(30),A(30),C(30)
DEFINE FILE 10(57,120,U,K00)
DEFINE FILE 101(41,93,U,K01)
DEFINE FILE 102(41,93,U,K02)
DEFINE FILE 103(41,93,U,K03)
DEFINE FILE 104(41,93,U,K04)
DEFINE FILE 105(41,93,U,K05)
DEFINE FILE 106(41,93,U,K06)
DEFINE FILE 107(41,93,U,K07)
DEFINE FILE 108(41,93,U,K08)
DEFINE FILE 109(41,93,U,K09)
DEFINE FILE 110(41,93,U,K10)
DEFINE FILE 111(41,93,U,K11)
DEFINE FILE 112(41,93,U,K12)
DEFINE FILE 113(41,93,U,K13)
DEFINE FILE 114(41,93,U,K14)
DEFINE FILE 115(41,93,U,K15)
DEFINE FILE 116(41,93,U,K16)
DEFINE FILE 117(41,93,U,K17)
DEFINE FILE 118(41,93,U,K18)
DEFINE FILE 119(41,93,U,K19)
DEFINE FILE 120(41,93,U,K20)
LI=8
LO=5
F=EXP(ALOG(100.0)/40.0)
X=0.1
1 READ (LI,2000) N,K
2000 FORMAT (2I2)
IF (N) 2,2,3
2 WRITE (LO,3000)
3000 FORMAT (' FIN')
CALL EXIT
3 CONTINUE
WRITE(LO,300)
300 FORMAT(1X,/)
DO 30 I=1,41
DO 10 J=1,N
A(J)=1.0
B(J)=-2.0
10 C(J)=1.0
B(K)=-1.0-X
C(K)=X
A(K+1)=X
B(K+1)=-1.0-X
CALL TRIII
CALL TRIRO
CALL TRIGR (V,6.0)
DO 15 J=1,N
CALL TRIEV (Z,J)
CALL TRINO (Z,N)
15 CALL TRIST (Z,N,100+J,I,6)
30 X=X*F
K1=K+1
WRITE (LO,400) N,K,K1
400 FORMAT(' GRAFICA DEL NEGATIVO DEL CUADRADO DE LAS FRE'
1'CUENCIAS DE RESONANCIA DE UNA CADENA HOMO-'/' GENEA '
2'DE',I2,' PARTICULAS,EN LA QUE SE MODIFICA SISTEMATICA'
3'MENTE LA K ENTRE LAS PARTICULAS',I2,' Y'/,I2,' ,LA '
4'VARIACION ES EN EL EJE VERTICAL.')
DO 32 I=1,N
CALL TRIPG (Z,N,0,10,1)
CALL TRIPG (Z,N,0,10,2)
DO 31 J=1,41
CALL TRIST (Z,N,100+I,J,5)
31 CALL TRIPG (Z,N,J,10,3)
32 CALL TRIPG (Z,N,0,10,5)
GO TO 1
END
// FOR
*LIST SOURCE PROGRAM
*IOOS(2501 READER,1403 PRINTER,DISK)
*ONE WORD INTEGERS
*EXTENDED PRECISION
*NAME TRIDI
C
C APENDICE E
C
C TRIDI ES UN PROGRAMA PRINCIPAL QUE VARIA LA RAZON DE
C MASAS DE UNA CADENA DIATOMICA, CONSIDERA TODAS LAS
C CONTANTES ELASTICAS IGUALES, CALCULA E IMPRIME LOS
C EIGENVALORES Y EIGENVECTORES PARA CADA INCREMENTO DE
C LA RAZON DE MASAS.
DIMENSION Z(31)
COMMON N,LI,LO,LP,LT,I0,X0,XN
COMMON V(31),Q(2,2)
COMMON B(30),A(30),C(30)
DEFINE FILE 10(57,120,U,K00)
DEFINE FILE 101(41,93,U,K01)
DEFINE FILE 102(41,93,U,K02)
DEFINE FILE 103(41,93,U,K03)
DEFINE FILE 104(41,93,U,K04)
DEFINE FILE 105(41,93,U,K05)
DEFINE FILE 106(41,93,U,K06)
DEFINE FILE 107(41,93,U,K07)
DEFINE FILE 108(41,93,U,K08)
DEFINE FILE 109(41,93,U,K09)
DEFINE FILE 110(41,93,U,K10)
DEFINE FILE 111(41,93,U,K11)
DEFINE FILE 112(41,93,U,K12)
DEFINE FILE 113(41,93,U,K13)
DEFINE FILE 114(41,93,U,K14)
DEFINE FILE 115(41,93,U,K15)
DEFINE FILE 116(41,93,U,K16)
DEFINE FILE 117(41,93,U,K17)
DEFINE FILE 118(41,93,U,K18)
DEFINE FILE 119(41,93,U,K19)
DEFINE FILE 120(41,93,U,K20)
LI=8
LO=5
F=EXP(ALOG(6.25)/40.0)
1 READ (LI,2000) N
2000 FORMAT (I2)
IF (N) 2,2,3
2 WRITE (LO,3000)
3000 FORMAT (59X,'FIN')
CALL EXIT
3 CONTINUE
WRITE(LO,300)
300 FORMAT(1X,/)
X=0.4
DO 30 K=1,41
DO 10 J=1,N
A(J)=1.0
C(J)=1.0
10 CONTINUE
DO 11 J=1,N,2
11 B(J)=-2.0/X
DO 12 J=2,N,2
12 B(J)=-2.0*X
CALL TRIII
CALL TRIRO
CALL TRIGR (V,6.0)
DO 15 I=1,N
CALL TRIEV (Z,I)
Y=SQRT(X)
DO 13 J=1,N,2
13 Z(J)=Z(J)/Y
DO 14 J=2,N,2
14 Z(J)=Z(J)*Y
CALL TRINO (Z,N)
15 CALL TRIST (Z,N,100+I,K,6)
30 X=X*F
WRITE (LO,400) N
400 FORMAT(' GRAFICA DEL NEGATIVO DEL CUADRADO DE LAS FRE'
1'CUENCIAS NATURALES DE UNA CADENA DIATOMICA'/' DE',I2,
2'PARTICULAS, DONDE SE VARIA LA RAZON DE MASAS EN EL
3'EJE VERTICAL.')
DO 32 I=1,N
CALL TRIPG (Z,N,0,10,1)
CALL TRIPG (Z,N,0,10,2)
DO 31 J=1,41
CALL TRIST (Z,N,100+I,J,5)
31 CALL TRIPG (Z,N,J,10,3)
32 CALL TRIPG (Z,N,0,10,5)
GO TO 1
END
// FOR
*LIST SOURCE PROGRAM
*IO0S(2501 READER,1403 PRINTER,DISK)
*ONE WORD INTEGERS
*EXTENDED PRECISION
*NAME TRIVD
C
C APENDICE F
C
C TRIVD ES UN PROGRAMA PRINCIPAL QUE VARIA LA MASA DE
C LA PARTICULA K DE UNA CADENA DIATOMICA CON RAZON DE
C MASAS R. CALCULA E IMPRIME LOS EIGENVALORES Y EIGEN-
C VECTORES PARA EL INTERVALO DE VARIACION DE LA MASA.
DIMENSION Z(31)
COMMON N,LI,LO,LP,LT,I0,X0,XN
COMMON V(31),Q(2,2)
COMMON B(30),A(30),C(30)
DEFINE FILE 10(57,120,U,K00)
DEFINE FILE 101(41,93,U,K01)
DEFINE FILE 102(41,93,U,K02)
DEFINE FILE 103(41,93,U,K03)
DEFINE FILE 104(41,93,U,K04)
DEFINE FILE 105(41,93,U,K05)
DEFINE FILE 106(41,93,U,K06)
DEFINE FILE 107(41,93,U,K07)
DEFINE FILE 108(41,93,U,K08)
DEFINE FILE 109(41,93,U,K09)
DEFINE FILE 110(41,93,U,K10)
DEFINE FILE 111(41,93,U,K11)
DEFINE FILE 112(41,93,U,K12)
DEFINE FILE 113(41,93,U,K13)
DEFINE FILE 114(41,93,U,K14)
DEFINE FILE 115(41,93,U,K15)
DEFINE FILE 116(41,93,U,K16)
DEFINE FILE 117(41,93,U,K17)
DEFINE FILE 118(41,93,U,K18)
DEFINE FILE 119(41,93,U,K19)
DEFINE FILE 120(41,93,U,K20)
LI=8
LO=5
F=EXP(ALOG(49.0)/40.0)
1 READ (LI,2000) N,K
2000 FORMAT (2I2)
IF (N) 2,2,3
2 CONTINUE
WRITE (LO,3000)
3000 FORMAT (59X,'FIN')
CALL EXIT
3 CONTINUE
WRITE(LO,300)
300 FORMAT(1X,/)
R=0.75
X=0.143
DO 20 I=1,41
DO 10 J=1,N
A(J)=1.0
10 C(J)=1.0
DO=11 J=1,N,2
11 B(J)=-2.0/R
DO 12 J=2,N,2
12 B(J)=-2.0*R
T=-2.0/(X*B(K))
Y=SQRT(T)
C(K-1)=C(K-1)*Y
A(K)=A(K)*Y
B(K)=B(K)*T
C(K)=C(K)*Y
A(K+1)=A(K+1)*Y
CALL TRIII
CALL TRIRO
CALL TRIGR (V,6.0)
DO 19 L=1,N
CALL TRIEV (Z,L)
S=SQRT(R)
DO 13 J=1,N,2
13 Z(J)=Z(J)/S
DO 15 J=2,N,2
15 Z(J)=Z(J)*S
Z(K)=Z(K)*Y
CALL TRINO (Z,N)
19 CALL TRIST (Z,N,100+L,I,6)
20 X=X*F
WRITE (LO,400) N,K
400 FORMAT (' GRAFICA DEL NEGATIVO DEL CUADRADO DE LAS FRE'
1'CUENCIAS NATURALES DE UNA CADENA DIATOMICA '/' DE',I2,
2' PARTICULAS VARIANDO EN EL EJE VERTICAL LA MASA DE LA'
3' PARTICULA',I2'.')
DO 32 I=1,N
CALL TRIPG (Z,N,0,10,1)
CALL TRIPG (Z,N,0,10,2)
DO 31 J=1,41
CALL TRIST (Z,N,100+I,J,5)
31 CALL TRIPG (Z,N,J,10,3)
32 CALL TRIPG (Z,N,0,10,5)
GO TO 1
END
// FOR
*LIST SOURCE PROGRAM
*IO0S(2501 READER,1403 PRINTER,DISK)
*ONE WORD INTEGERS
*EXTENDED PRECISION
*NAME TRIVL
C
C APENDICE G
C
C TRIVL ES UN PROGRAMA PRINCIPAL QUE VARIA LA DIFERENCIA
C DE LA SUCESION ARITMETICA QUE SIGUEN LAS MASAS DE UNA
C CADENA UNIDIMENSIONAL, EN LA QUE TODAS LAS CONSTANTES
C ELASTICAS SON IGUALES. CALCULA E IMPRIME LOS EIGENVALO-
C RES Y EIGENVECTORES PARA EL INTERVALO DE VARIACION DE
C ESTA DIFERENCIA.
DIMENSION Z(31)
COMMON N,LI,LO,LP,LT,I0,X0,XN
COMMON V(31),Q(2,2)
COMMON B(30),A(30),C(30)
DEFINE FILE 10(57,120,U,K00)
DEFINE FILE 101(41,93,U,K01)
DEFINE FILE 102(41,93,U,K02)
DEFINE FILE 103(41,93,U,K03)
DEFINE FILE 104(41,93,U,K04)
DEFINE FILE 105(41,93,U,K05)
DEFINE FILE 106(41,93,U,K06)
DEFINE FILE 107(41,93,U,K07)
DEFINE FILE 108(41,93,U,K08)
DEFINE FILE 109(41,93,U,K09)
DEFINE FILE 110(41,93,U,K10)
DEFINE FILE 111(41,93,U,K11)
DEFINE FILE 112(41,93,U,K12)
DEFINE FILE 113(41,93,U,K13)
DEFINE FILE 114(41,93,U,K14)
DEFINE FILE 115(41,93,U,K15)
DEFINE FILE 116(41,93,U,K16)
DEFINE FILE 117(41,93,U,K17)
DEFINE FILE 118(41,93,U,K18)
DEFINE FILE 119(41,93,U,K19)
DEFINE FILE 120(41,93,U,K20)
LI=8
LO=5
1 READ (LI,200) N
200 FORMAT (I2)
IF (N) 2,2,3
2 CALL EXIT
3 CONTINUE
WRITE (LO,300)
300 FORMAT (1H1)
X=1.0
DO 30 K=1,41
B=2.0*(1.0-X)/(N-1)
DO 10 J=1,N
XJ=J-1
A(J)=1.0/SQRT((X+(XJ-1.0)*B)*(X+XJ*B))
B(J)=-2.0/(X+XJ*B)
C(J)=1.0/SQRT((X+XJ*B)*(X+(XJ+1.0)*B))
10 CONTINUE
CALL TRIII
CALL TRIRO
CALL TRIGR (V,6.0)
DO 12 I=1,N
CALL TRIEV (Z,I)
DO 11 J=1,N
XJ=J-1
1 Z(J)=Z(J)/SQRT(X+XJ*B)
CALL TRINO (Z,N)
12 CALL TRIST (Z,N,100+I,K,6)
30 X=X-0.02
WRITE (LO,400) N
400 FORMAT ('GRAFICA DEL NEGATIVO DEL CUADRADO DE LAS FRE'
1'CUENCIAS NATURALES DE UNA CADENA UNIDI-'/' MENSIONAL'
2' DE',I2,' PARTICULAS, EN LA QUE SUS MASAS VARIAN COMO'
3' UNA SUCESION ARITMETICA,'/' EN EL EJE VERTICAL SE VA'
4' RIA LA DIFERENCIA DE DICHA SUCESION.')
DO 32 I=1,N
CALL TRIPG (Z,N,0,10,1)
CALL TRIPG (Z,N,0,10,2)
DO 31 K=1,41
CALL TRIST (Z,N,100+I,K,5)
31 CALL TRIPG (Z,N,K,10,3)
32 CALL TRIPG (Z,N,0,10,5)
GO TO 1
END
// FOR
*LIST SOURCE PROGRAM
*IO0S(2501 READER, 1403 PRINTER,DISK)
*ONE WORD INTEGERS
*EXTENDED PRECISION
*NAME TRIVE
C
C APENDICE H
C
C TRIVE ES EL PROGRAMA PRINCIPAL QUE VARIA SISTEMATICA-
C MENTE LAS MASAS DE LAS PARTICULAS EN TAL FORMA QUE LA
C MASA TOTAL DE LA CADENA PERMANECE CONSTANTE, PERO CON
C UNA RAZON FIJA ENTRE UNA MASA Y LA SIGUIENTE. CALCULA
C E IMPRIME LOS EIGENVALORES Y EIGENVECTORES PARA EL IN-
C TERVALO DE VARIACION DE ESTA RAZON.
DIMENSION Z(31)
COMMON N,LI,LO,LP,LT,I0,X0,XN
COMMON V(31),Q(2,2)
COMMON B(30),A(30),C(30)
DEFINE FILE 10(57,120,U,K00)
DEFINE FILE 101(41,93,U,K01)
DEFINE FILE 102(41,93,U,K02)
DEFINE FILE 103(41,93,U,K03)
DEFINE FILE 104(41,93,U,K04)
DEFINE FILE 105(41,93,U,K05)
DEFINE FILE 106(41,93,U,K06)
DEFINE FILE 107(41,93,U,K07)
DEFINE FILE 108(41,93,U,K08)
DEFINE FILE 109(41,93,U,K09)
DEFINE FILE 110(41,93,U,K10)
DEFINE FILE 111(41,93,U,K11)
DEFINE FILE 112(41,93,U,K12)
DEFINE FILE 113(41,93,U,K13)
DEFINE FILE 114(41,93,U,K14)
DEFINE FILE 115(41,93,U,K15)
DEFINE FILE 116(41,93,U,K16)
DEFINE FILE 117(41,93,U,K17)
DEFINE FILE 118(41,93,U,K18)
DEFINE FILE 119(41,93,U,K19)
DEFINE FILE 120(41,93,U,K20)
LP=2
LI=8
LO=5
1 READ (LI,2000) N
2000 FORMAT (I2)
IF (N) 2,2,3
2 WRITE (LO,3000)
3000 FORMAT (59X,'FIN')
CALL EXIT
3 CONTINUE
WRITE (LO,300)
300 FORMAT(1X,/)
R=1.0-1.0E-8
DO 30 K=1,41
F=N*(1.0-R)/(1.0-R**N)
S=SQRT(R)
X=F
DO 10 J=1,N
A(J)=S/X
B(J)=-2.0/X
C(J)=1.0/(S*X)
10 X=R*X
CALL TRIII
CALL TRIRO
CALL TRIGR (V,6.0)
DO 15 I=1,N
CALL TRIEV (Z,I)
X=SQRT(F)
DO 12 J=1,N
Z(J)=Z(J)/X
12 X=X*S
CALL TRINO (Z,N)
15 CALL TRIST (Z,N,100+I,K,6)
30 R=R-0.018
WRITE (LO,400) N
400 FORMAT (' GRAFICA DEL NEGATIVO DEL CUADRADO DE LAS FRE'
1'CUENCIAS DE RESONANCIA DE UNA CADENA DE'/,1X,I2,' PAR'
2'TICULAS, EN LA QUE SUS MASAS VARIAN COMO UNA EXPONEN'
3'CIAL DECRECIENTE, EN EL EJE'/' VERTICAL SE VARIA LA '
4'RAZON, SE CONSIDERA LA MASA TOTAL CONSTANTE.')
DO 32 I=1,N
CALL TRIPG (Z,N,0,10,1)
CALL TRIPG (Z,N,0,10,2)
DO 31 K=1,41
CALL TRIST (Z,N,100+I,K,5)
31 CALL TRIPG (Z,N,K,10,3)
32 CALL TRIPG (Z,N,0,10,5)
GO TO 1
END
// FOR
*LIST SOURCE PROGRAM
*IO0S(2501 READER,1403 PRINTER,DISK)
*ONE WORD INTEGERS
*EXTENDED PRECISION
*NAME TRIVG
C
C APENDICE I
C
C TRIVG ES EL PROGRAMA PRINCIPAL QUE VARIA LA MASA DE LAS
C PARTICULAS DE UNA CADENA LINEAL EN FORMA GAUSSIANA
C EXP(-((X-X0)/A)**2)
C CALCULA E IMPRIME LOS EIGENVALORES Y EIGENVECTORES PARA
C UN INTERVALO DE LA VARIANCIA A.
REAL MA(30)
DIMENSION Z(31)
DIMENSION AM(32)
COMMON N,LI,LO,LP,LT,I0,X0,XN
COMMON V(31),Q(2,2)
COMMON B(30),A(30),C(30)
EQUIVALENCE (MA(1),AM(2))
DEFINE FILE 10(57,120,U,K00)
DEFINE FILE 101(41,93,U,K01)
DEFINE FILE 102(41,93,U,K02)
DEFINE FILE 103(41,93,U,K03)
DEFINE FILE 104(41,93,U,K04)
DEFINE FILE 105(41,93,U,K05)
DEFINE FILE 106(41,93,U,K06)
DEFINE FILE 107(41,93,U,K07)
DEFINE FILE 108(41,93,U,K08)
DEFINE FILE 109(41,93,U,K09)
DEFINE FILE 110(41,93,U,K10)
DEFINE FILE 111(41,93,U,K11)
DEFINE FILE 112(41,93,U,K12)
DEFINE FILE 113(41,93,U,K13)
DEFINE FILE 114(41,93,U,K14)
DEFINE FILE 115(41,93,U,K15)
DEFINE FILE 116(41,93,U,K16)
DEFINE FILE 117(41,93,U,K17)
DEFINE FILE 118(41,93,U,K18)
DEFINE FILE 119(41,93,U,K19)
DEFINE FILE 120(41,93,U,K20)
LI=8
LO=5
1 READ (LI,2000) N
2000 FORMAT (I2)
IF (N) 2,2,3
2 WRITE (LO,3000)
3000 FORMAT (59X,'FIN')
CALL EXIT
3 CONTINE
WRITE(LO,300)
300 FORMAT (1H1)
XL=-2.0
XR=2.0
DX=(XR-XL)/FLOAT(N-1)
ALFA=-0.5
ALFA=0.0
DO 20 M=1,41
AM(1)=1.0
DO 5 J=1,N
5 MA(J)=EXP(-ALFA*(XL+(J-1)*DX)**2)
AM(N+2)=1.0
CALL TRINO (MA,N)
F=SQRT(FLOAT(N))
DO 6 J=1,N
6 MA(J)=MA(J)*F
DO 7 J=1,N
7 MA(J)=SQRT(MA(J))
DO 10 J=1,N
A(J)=1.0/(AM(J)*AM(J+1))
B(J)=-2.0/(MA(J)*MA(J))
C(J)=1.0/(AM(J+1)*AM(J+2))
10 CONTINUE
CALL TRIII
CALL TRIRO
CALL TRIGR (V,6.0)
DO 12 I=1,N
CALL TRIEV (Z,I)
DO 11 J=1,N
11 Z(J)=Z(J)/MA(J)
CALL TRINO (Z,N)
12 CALL TRIST (Z,N,100+I,M,6)
20 ALFA=ALFA+0.015
WRITE (LO,400) N
400 FORMAT ('GRAFICA DEL NEGATIVO DEL CUADRADO DE LAS FRE'
1' CUENCIAS DE RESONANCIA DE UNA CADENA LINEAL'/' DE',I2,
2' PARTICULAS EN LA QUE SUS MASAS SE VARIAN COMO UNA DI'
3' STRIBUCION GAUSSIANA'/' EXP(-((X-XO)/A)**2), EN EL EJE'
4' VERTICAL SE VARIA LA VARIANCIA A.')
CALL TRIGE
GO TO 1
END
Next: Referencias
Up: Diversos aspectos de la
Previous: Condición para obtener los
Contents
Pedro Hernandez
2006-02-20