



Next: Conclusiones
Up: Diversos aspectos de la
Previous: Parametrización de rotaciones hiperbólicas
Contents
En el Cap. II vimos que la condición para obtener los
Eigenvalores 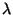 era que la matriz resultante del producto
de todas las Matrices de Transferencia tuviera su elemento (1,1)
igual a cero, ahora veamos en cual condición se transforma la
anterior en la Representación Vectorial de las Matrices
Unimodulares.
Supongamos que el
era que la matriz resultante del producto
de todas las Matrices de Transferencia tuviera su elemento (1,1)
igual a cero, ahora veamos en cual condición se transforma la
anterior en la Representación Vectorial de las Matrices
Unimodulares.
Supongamos que el  es el ``vector'' que representa a la suma total
de los distintos ``vectores'' que representan a las Matrices de
Transferencia
es el ``vector'' que representa a la suma total
de los distintos ``vectores'' que representan a las Matrices de
Transferencia
por otra parte de la Ec. (IV.10') se tiene
 |
(IV.34) |
si expresamos a 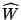 como
como
y luego sustituímos en (IV.34), se tiene
para que existan eigenvalores 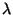 se tiene que
cumplir que
se tiene que
cumplir que  , lo que implica de la Ec. de arriba
, lo que implica de la Ec. de arriba
por lo tanto
 |
(IV.35) |
finalmente si sustituímos la Ec. anterior en la
expresión para  se tiene
se tiene
o también
 |
(IV.36) |
entonces la condición para que existan Eigenvalores
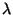 es
es
 |
(IV.37) |




Next: Conclusiones
Up: Diversos aspectos de la
Previous: Parametrización de rotaciones hiperbólicas
Contents
Pedro Hernandez
2006-02-20