



Next: Dinámica de una red
Up: Breve análisis de vibraciones
Previous: Interpretación de los eigenvalores
Contents
Esencialmente se tienen tres problemas de eigenvalores
distintos por resolver, en este enfoque para las vibraciones de
una cadena lineal, y que son:
- La determinación de las frecuencias naturales o de
resonancia
y los modos normales de vibración, que implica hallar los
eigenvalores
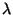 y los eigenvectores
y los eigenvectores 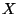 de la matriz de
movimiento
de la matriz de
movimiento 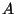 .
.
- La determinación de los números de onda de los modos
normales y ondas, que significa encontrar los eigenvalores
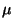 y eigenvectores
y eigenvectores 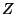 de la matriz de Transferencia
de la matriz de Transferencia 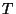 .
.
- La determinación del vector aniquilado por la submatriz de
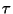 , que únicamente puede ocurrir para ciertas frecuencias.
, que únicamente puede ocurrir para ciertas frecuencias.
Mucho del análisis de la interacción general hasta el
k-ésimo vecino, se simplifica enormemente si uno considera
únicamente interacciones a primeros vecinos, en los
capítulos siguientes es el único tipo de interacciones
que se analizan, ya que 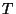 es de dimensión 2 y la
ecuación (I.17) es un simple polinomio y no una ecuación
determinantal.
es de dimensión 2 y la
ecuación (I.17) es un simple polinomio y no una ecuación
determinantal.




Next: Dinámica de una red
Up: Breve análisis de vibraciones
Previous: Interpretación de los eigenvalores
Contents
Pedro Hernandez
2006-02-20