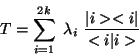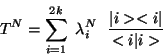Next: Conclusiones
Up: Breve análisis de vibraciones
Previous: Matriz de transferencia
Contents
Es conveniente, examinar los eigenvalores y eigenvectores de la
matriz de Transferencia 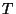 , es decir, considerar un segundo
problema de eigenvalores.
, es decir, considerar un segundo
problema de eigenvalores.
 |
(I.18) |
así, cuando 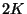 desplazamientos sucesivos forman
un eigenvector de
desplazamientos sucesivos forman
un eigenvector de 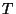 , se tiene que cada componente es
multiplicada por el factor
, se tiene que cada componente es
multiplicada por el factor 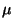 al pasar de una partícula a
la siguiente. La interpretación natural de estos eigenvectores
es que definen la descomposición de los desplazamientos de las
partículas de ondas, cuya constante de propagación es
al pasar de una partícula a
la siguiente. La interpretación natural de estos eigenvectores
es que definen la descomposición de los desplazamientos de las
partículas de ondas, cuya constante de propagación es
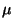 . Como
. Como 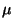 puede ser real o complejo, imaginario, de
módulo 1 ó diferente; es posible distinguir la propagación
de ondas, de forma creciente o decreciente, oscilaciones, o una
mezcla, respectivamente.
A menudo el logaritmo de
puede ser real o complejo, imaginario, de
módulo 1 ó diferente; es posible distinguir la propagación
de ondas, de forma creciente o decreciente, oscilaciones, o una
mezcla, respectivamente.
A menudo el logaritmo de 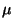 es más útil
es más útil
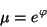 |
(I.19) |
y a 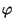 es a lo que se le denomina como
número de onda de Z.
En el caso de una cadena homogénea, ya hemos visto que
es a lo que se le denomina como
número de onda de Z.
En el caso de una cadena homogénea, ya hemos visto que
Entonces teniendo los eigenvalores y eigenvectores de 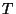 uno
puede aplicar el Teorema Espectral para expresar a
uno
puede aplicar el Teorema Espectral para expresar a 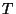 como
como
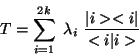 |
(I.20) |
donde
es el operador de Proyección para el eigenvalor
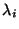 , en el caso de que lo eigenvectores no estén
normalizados.
Con lo anterior es muy fácil calcular cualquier potencia de
, en el caso de que lo eigenvectores no estén
normalizados.
Con lo anterior es muy fácil calcular cualquier potencia de
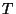 , ya que si uno aplica el Teorema de Sylvester, se tiene
, ya que si uno aplica el Teorema de Sylvester, se tiene
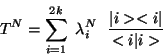 |
(I.21) |




Next: Conclusiones
Up: Breve análisis de vibraciones
Previous: Matriz de transferencia
Contents
Pedro Hernandez
2006-02-20