


Next: Matriz de transferencia
Up: Dinámica de una red
Previous: Dinámica de una red
Contents
En el caso en que únicamente existen interacciones a
primeros vecinos, es decir, se considera que las masas están
ligadas por resortes a sus vecinos más próximos, como lo
muestra la figura
la ecuación de movimiento para la partícula 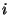 es
es
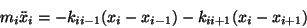 |
(II.1) |
si denotamos
se tiene
 |
(II.2) |
Al igual que en el Cap. anterior, suponemos que existen ahora
únicamente dos partículas ficticias, una a cada lado de la
red y cuyos desplazamientos son idénticamente cero, por lo que
la ecuación (II.2) es válida para toda
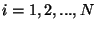 .
Entonces el conjunto de Ecs. (II.2) dan lugar a un sistema de
Ecs. diferenciales, con una matriz de coeficientes
Tridiagonal, explícitamente se tiene
.
Entonces el conjunto de Ecs. (II.2) dan lugar a un sistema de
Ecs. diferenciales, con una matriz de coeficientes
Tridiagonal, explícitamente se tiene
![\begin{displaymath}
\left [ \begin{array}{c}
m_{1} \ddot{x}_{1} \\
m_{2} \d...
...
x_{1} \\
x_{2} \\
\vdots \\
x_{N}
\end{array} \right]
\end{displaymath}](img89.png) |
(II.3) |
Como estamos considerando que las masa de las partículas
son distintas, nos conviene hacer la transformación del
capítulo anterior.
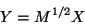 |
(II.4) |
donde 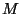 es la misma matriz diagonal de antes, y
es la misma matriz diagonal de antes, y 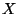 sigue siendo el vector de los desplazamientos de las
partículas.
Así, si
sigue siendo el vector de los desplazamientos de las
partículas.
Así, si 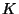 es la matriz de los coeficientes elásticos,
se tiene
es la matriz de los coeficientes elásticos,
se tiene
 |
(II.5) |
donde los elementos de la matriz
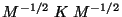 son de la forma
son de la forma
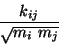 |
(II.6) |
Si denotamos a la matriz de arriba por 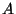 , la Ec. de
movimiento para la cadena, en el sistema de coordenadas definidas
(II.4) es
, la Ec. de
movimiento para la cadena, en el sistema de coordenadas definidas
(II.4) es
![\begin{displaymath}
\frac{d^{2}}{d t^{2}} \left [ \begin{array}{c}
y_{1} \\
...
...
y_{1} \\
y_{2} \\
\vdots \\
y_{N}
\end{array} \right]
\end{displaymath}](img93.png) |
(II.7) |
Ahora bien, la cadena puede tener sus extremos fijos a una
pared, que es como se ha considerado, pero de las Ecs. (II.2)
es claro, que para analizar una cadena con sus extremos libres
sólo hay que modificar los elementos 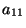 y
y 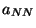 , ya que si para
extremos confinados sus valores eran
, ya que si para
extremos confinados sus valores eran
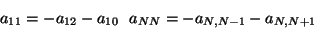 |
(II.8) |
ahora son
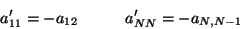 |
(II.9) |
y para el caso de una combinación, es decir, un
extremo libre y otro confinado, se elige una constante de (II.8) y
otra de (II.9) según sea el caso.
El que uno sólo tenga que modificar los elementos 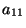 y
y 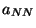 es un
resultado de haber introducido las partículas ficticias.
Si suponemos que
es un
resultado de haber introducido las partículas ficticias.
Si suponemos que 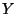 es eigenvector de
es eigenvector de 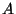 , se tiene
, se tiene
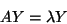 |
(II.10) |
o también
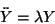 |
(II.11) |
entonces nuestro problema consiste en obtener los
eigenvalores y eigenvectores de 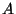 , ya que la Ec. (II.11) se
reconoce como una Ec. diferencial para los Modos Normales de
Vibración y los
, ya que la Ec. (II.11) se
reconoce como una Ec. diferencial para los Modos Normales de
Vibración y los 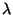 son precisamente las frecuencias
naturales o de resonancia para el Sistema, la resolución del
problema por métodos analíticos en el caso general no es
posible, excepto para el caso de una cadena homogénea, en el que
sí es posible hallar la solución analítica, para los
demás casos hay necesidad de utilizar métodos numéricos para
obtener el espectro de frecuencias y los Modos Normales de
Vibración.
son precisamente las frecuencias
naturales o de resonancia para el Sistema, la resolución del
problema por métodos analíticos en el caso general no es
posible, excepto para el caso de una cadena homogénea, en el que
sí es posible hallar la solución analítica, para los
demás casos hay necesidad de utilizar métodos numéricos para
obtener el espectro de frecuencias y los Modos Normales de
Vibración.



Next: Matriz de transferencia
Up: Dinámica de una red
Previous: Dinámica de una red
Contents
Pedro Hernandez
2006-02-20
![\includegraphics[width=5in]{f02p16.eps}](img85.png)
![\includegraphics[width=5in]{f02p16.eps}](img85.png)
![\begin{displaymath}
\left [ \begin{array}{c}
m_{1} \ddot{x}_{1} \\
m_{2} \d...
...
x_{1} \\
x_{2} \\
\vdots \\
x_{N}
\end{array} \right]
\end{displaymath}](img89.png)
![\begin{displaymath}
\frac{d^{2}}{d t^{2}} \left [ \begin{array}{c}
y_{1} \\
...
...
y_{1} \\
y_{2} \\
\vdots \\
y_{N}
\end{array} \right]
\end{displaymath}](img93.png)