Logaritmo de la misma clase de matrices.

Por un procedimiento similar, consideremos el logaritmo de una matriz cuyos eigenvalores ocurren en parejas recíprocas, esto es:

$$\ln T=\sum_{i=-n}^n \ln\mu_i\Gamma_i =\sum_{i>0}\ln\mu_i \: [\Gamma_i -\Gamma_{-1} ]$$

En donde:

$$\Gamma_i -\Gamma_{-i} =\frac{T^{n-1}}{\,{\mbox{senh}}\phi_i} \: \gamma_i \: [T\cosh (n-1)\phi_i -II\cosh n\phi_i ]$$

En donde hemos empleado la definición $\mu_i +\mu_{-i} = 2\cosh\phi_i$, por lo tanto resulta:

$$\ln T=\sum_{i>0} \ln\mu_i \frac{T^{n-1}}{\,{\mbox{senh}}\phi_i} \: \{ T\cosh(n-1)\phi_i -\cosh n\phi_i \} \: \gamma_i$$

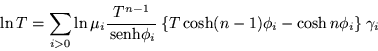
Es conveniente mencionar, que todos estos cálculos serán empleados posteriormente.