Teorema acerca de las raíces en parejas recíprocas.

Analicemos como elevar a una potencia, una matriz cuya ecuación característica tiene raíces que ocurren en parejas recíprocas.

En primer lugar, tomaremos una matriz con las características mencionadas anteriormente y obtendremos sus eigenvalores y eigenvectores; el método es un artificio matemático, en el sentido de que ésta es una forma de elevar una matriz a una potencia muy grande, este método se basa en el cálculo de los eigenvalores y eigenvectores para lo cual se puede aplicar el teorema de Silvester y obtener con ello, que una matriz se puede expresar como una función de sus eigenvalores, elevados a una cierta potencia, por sus operadores idempotentes.

Por lo tanto lo que nos interesa es obtener una fórmula, para matrices cuyas raíces ocurren en parejas recíprocas que nos permita elevarla a una cierta potencia.

Nuestra hipótesis es que, para todo eigenvalor $\mu$, $1/\mu$ es también un eigenvalor, es por lo tanto conveniente numerar los eigenvalores de $-N/2$ ($=n$) a $N/2$, en donde $N$ es la dimensión de la matriz, además es necesario eliminar algunos casos excepcionales como: $\mu =0$ que no tiene inverso, y $\mu =1$ que da lugar a un par degenerado. Si una matriz posee tales eigenvalores, no podemos trabajar en su subespacio complementario usando técnicas bien establecidas. También supondremos que la matriz tiene un conjunto de eigenvectores, así que las fórmulas

$$T = \sum_{i=1}^n \mu_i \Gamma_i$$ (3.10)

$$\Gamma_i = \frac{\prod_{\mu_j\neq\mu_i} (T-\mu_j II)} {\prod_{j\neq i}(\mu_i -\mu_j )}$$ (3.11)

Son válidas en términos de los eigenvalores $\mu_i$ y operadores de proyección $\Gamma_i$. Cuando existen eigenvectores repetidos hay que cambiar la condición de que $\mu_i\neq\mu_j$ ya que el denominador es el producto de las diferencias de distintos eigenvalores y no de los índices, pero por el momento supondremos que todos estos eigenvectores son distintos (la demostración de la validez de (3.10) y (3.11) pueden verse en el apéndice B trabajando con (3.11), tomando en cuenta que, los eigenvalores ocurren en parejas recíprocas resulta:

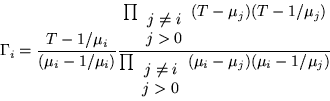$$\Gamma_i =\frac{T-1/\mu_i}{(\mu_i -1/\mu_i)} \frac{\prod_{... ...j\neq i \\ j>0 \end{array}} (\mu_i -\mu_j)(\mu_i -1/ \mu_j) }$$ (3.12)

Multiplicando explícitamente los factores y denotando los eigenvalores recíprocos por $\mu_{-i},\; \mu_{-j}$ resulta

$$\Gamma_i =\frac{T-\mu_{-i}}{(\mu_i -\mu_{-i})} \frac{\pro... ... i \\ j>0 \end{array}} [\mu_i^2 -\mu_i\:(\mu_j+\mu_{-j}) +1]}$$ (3.13)

Esta ecuación nos indica la conveniencia de emplear las definiciones de funciones hiperbólicas esto es:

$$\mu_i +\mu_{-i} =2\cosh\phi_i \qquad \mbox{\hspace{.2in}y\hspace{.2in}} \qquad \mu_i -\mu_{-i} =2\,{\mbox{senh}}\phi_i$$

en cuyo caso resulta $\mu =e^{\phi}$ como se había empleado con anterioridad, también es conveniente definir.

$$T+T^{-1} =2\cosh\Phi$$ (3.14)

donde $\cosh\Phi$ es una matriz, que está definida en los mismos términos de la fórmula espectral. Por lo tanto con estas equivalencias y suponiendo que todas las raíces son distintas, la ecuación (3.13) se transforma en:

$$\Gamma_i =\frac{T^{n-1}}{\mu_i^{n-1}} \frac{T-\mu_{-i}}{2\,... ...ray}{c} j\neq i \\ j>0 \end{array}}(\cosh\phi_i -\cosh\phi_j)}$$

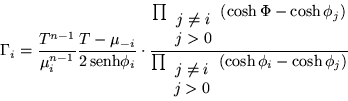
Consideremos la fórmula para $\Gamma_{-i}$:

$$\Gamma_{-i}=\frac{T-\mu_i}{\mu_{-i} -\mu_i} \frac{\prod_{... ...q i \\ j>0 \end{array}} (\mu_{-i} -\mu_j)(\mu_{-i} -\mu_{-j})}$$ (3.15)

Por un procedimiento similar resulta finalmente:

$$\Gamma_{-i} =\frac{T^{n-1}}{\mu_i^{-(n-1)}}\cdot\frac{T-\mu_... ...ay}{c} j\neq i \\ j>0 \end{array}} [\cosh\phi_i -\cosh\phi_j]}$$ (3.16)

Notemos que la matriz $\cosh\Phi$ tiene como eigenvalores $\cosh\phi_i$, así que los productos, en las fórmulas para $\Gamma_i$ y $\Gamma_{-i}$, son justamente los operadores de proyección para $\cosh\Phi$, esto es:

$$\gamma_i =\gamma_{-i} = \frac{\prod_{j\neq i} [\cosh\Phi -\cosh\phi_j]} {\prod_{j\neq i} [\cosh\phi_i -\cosh\phi_j]}$$

La diferencia entre $\Gamma_i$ y $\Gamma_{-i}$, es por supuesto el reemplazamiento de $\mu_i$ por $\mu_{-i}$ y el signo menos involucrado en el $\,{\mbox{senh}}$.

En el empleo de la resolución espectral (ver apéndice) para calcular la función de $T$, estamos interesados en el cálculo de potencias de $T$ este interés es debido al empleo directo que se puede hacer, en la condición que resultó para calcular los eigenvalores esto es, (2.17); por lo tanto lo que deseamos calcular en forma explícita es:

$$T^K =\sum_{i=-n}^n\mu_i^K \Gamma_i$$

la base de esto es suponer, que existe un conjunto completo de eigenvectores y por lo consiguiente en el caso no degenerado que todos los eigenvalores son distintos, ya que en este caso tendremos que existe un eigenvector para cada eigenvalor lo cual garantiza un número igual a la dimensión, por lo tanto:

Para un eigenvalor $\mu_1$ existe otro $1/ \mu_1$

Para un eigenvalor $\mu_2$ existe otro $1/ \mu_2$ etc.

Es conveniente denotar a los recíprocos como $\mu_{-1},\mu_{-2},\ldots ,$ con lo cual

$$T^K =\sum_{i=1}^{n=n/2} \{\mu_i^K \Gamma_i +\mu_{-i}^K \Gamma_i\}$$ (3.17)

Por otra parte para el caso que estamos tratando, los operadores de proyección (ver apéndice), están dados por:

$$\Gamma_i =\frac{T-\mu_i^{-1}}{2\,{\mbox{senh}}\phi_i}\frac{... ...,{\mbox{senh}}\phi_i}\frac{T^{n-1}}{\mu_i^{-(n+1)}} \gamma_i$$ (3.18)

En donde el operador $\gamma_i$ está definido como:

$$\gamma_i =\frac{\prod_{i<j}^n (\cosh\Phi -\cosh\phi_j)} {\prod_{i\neq j}^n (\cosh\phi_i -\cosh\phi_j)}= \gamma_{-i}$$ (3.19)

Sustituyendo los operadores dados por (3.18) y (3.19) en la ecuación (3.17) obtenemos

$$T^K=\sum_{i>0}^{n=N/2} \left[\mu_i^K \frac{T-\mu_i^{-1}}{... ...x{senh}}\phi_i}\frac{T^{n-1}}{\mu_i^{-(n-1)}}\gamma_i \right]$$

factorizando parcialmente tomando en cuenta que $T^{n-1}$ no depende del índice de la suma:

$$T^K=T^{n-1}\sum_{i=1}^n\frac{1}{2\,{\mbox{senh}}\phi_i} \l... ...-(K-n+1)}] -II[\mu_i^{K-n} -\mu_i^{-(K-n)}]\right\} \gamma_i$$

Podemos reducir finalmente la ecuación, usando la definición de $\mu$, esto es $\mu =e^{\phi}$, junto con el hecho de que $T$ tiene inverso:

$$T^{K-n+1} =\sum_{i=1}^n \left\{ T\frac{\,{\mbox{senh}}(K-... ...ox{senh}}(K-n)\phi_i}{\,{\mbox{senh}}\phi_i} \right\} \gamma_i$$ (3.20)

definifiendo $m = K-n+1$ y sustituyendo en (3.20) resulta

$$T^m =\sum_{i=1}^n \left\{T\frac{\,{\mbox{senh}}m\phi_i}{\,{... ...x{senh}}(m-1)\phi_i}{\,{\mbox{senh}}\phi_i} \right\} \gamma_i$$

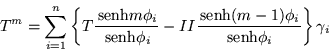
Que es finalmente la ecuación que nos permite calcular la matriz de transferencia a la enésima potencia.

Otra forma de la matriz $T^m$, se obtiene redefiniendo $m=K-n$ y multiplicando la ecuación obtenida por $T^{-1}$ con lo que resulta:

$$Q^m =\sum_{i=1}^n \left\{ II\frac{\,{\mbox{senh}}(m+1)\:\ph... ...\mbox{senh}}m\phi_i}{\,{\mbox{senh}}\phi_i} \right\} \gamma_i$$ (3.21)

Y una tercera forma, que es conveniente tener para cálculos posteriores, es la que se obtiene de sumar las ecuaciones (3.20) y (3.21), y de emplear la relación trigonométrica:

$$\,{\mbox{senh}}(m+1)\phi_i -\,{\mbox{senh}}(m-1)\phi_i =2\cosh m\phi_i \,{\mbox{senh}}\phi_i$$

y además la definición $T-T^{-1} =2\,{\mbox{senh}}\Phi$, en donde $\Phi$ es una matriz (ver apéndice) de estas ecuaciones resulta:

$$Q^m =\sum_{i=1}^n \left\{ II\cosh m\phi_i -\,{\mbox{senh}... ...{\mbox{senh}}m\phi_i}{\,{\mbox{senh}}\phi_i} \right\} \gamma_i$$

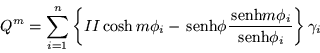
O sea tenemos tres fórmulas alternativas, para el caso en que queramos elevar a una potencia arbitraria una matriz también arbitraria, pero que cumple con las condiciones de que los eigenvalores se sucedan en parejas recíprocas y otras condicioes señaladas en el teorema, es conveniente señalar que el índice de la sumatoria se fija como la dimensión sobre dos, así por ejemplo cuando se trata de una matriz $2\times 2$, entonces $N=2$ y $n=N/2 =1$, por lo tanto existirá un solo término dado por $T^{-1}$ y no existirá el factor $\gamma_1$ además este caso partícular, se reduce al caso desarrollado con anterioridad el cual depende únicamente de si existen dos eigenvalores distintos. El desarrollo del caso que nos interesa de vibraciones a segundos vecinos, da lugar a matrices de $4\times 4$ por lo tanto $N=4 \;\rightarrow \;n=2$.