Debido a que este modelo es relativamente fácil, ya que su solución no depende del tipo de interacción que se esté llevando a cabo, entonces analizamos el caso general, pero que nos permite particularizar para el caso de interacciones a segundos vecinos, como se verá posteriormente.
Por lo tanto consideramos un sistema de masas y resortes con 
partículas, en el cual exigimos que las amplitudes de las
partículas 
sean cero, (para interacciones a segundos
vecinos serán las 
y 
) así como también las de las
partículas 
y 
, no todos los modos normales cumplirán
con tales condiciones, desde luego lo que podría ser esperado,
son los ceros en una onda en puntos diametralmente opuestos debido a
los requerimientos de simetría.
Por lo tanto nosotros empleamos las condicines cíclicas a
la frontera de Born-Kármán, esto es que:
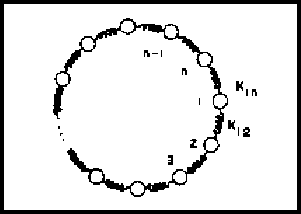
Por otra parte, podemos considerar los desplazamientos normales al plano, ya que se sigue con un problema unidimensional, la ventaja de discutir estos anillos, es que su solución analítica es relativamente fácil, ya que su relación de dispersión, que es lo que interesa obtener en primer lugar, se puede escribir en función de una serie de Fourier y una suma de potencias de cosenos, y más que ésto, podemos encontrar los eigenvalores y eigenvectores en el sentido del número de onda, pero es un poco restringido ya que las soluciones siempre van a salir cosenos y senos, por lo tanto vamos a ver ondas del tipo oscilatorio, ya que la amplitud, no puede aumentar ni disminuir, es decir, es constante, porque cuando iniciamos el ciclo con una amplitud determinada, tenemos forzosamente que llegar a donde iniciamos el ciclo con esa amplitud, entonces el movimiento ondulatorio es el único tipo de movimiento posible, o sea que como modelo no es realista ya que no nos permite obtener las amplitudes de las ondas, pero es conveniente solucionar el sistema por los resultados a que da lugar y también por la perturbación pequeña que se obtiene.