![\begin{displaymath}
M_c =\left[\begin{array}{llllll}
a_0 & a_1 & a_2 & a_3 & ...
...ots & a_{n-3} \\
\vdots & & & & \vdots
\end{array}\right]
\end{displaymath}](img620.gif)
La matriz de movimiento que describe el sistema esta dada por:
![\begin{displaymath}
M_c =\left[\begin{array}{llllll}
a_0 & a_1 & a_2 & a_3 & ...
...ots & a_{n-3} \\
\vdots & & & & \vdots
\end{array}\right]
\end{displaymath}](img620.gif)
Por lo tanto tenemos un tipo de matrices en cuya forma muy
general vemos: La diagonal principal es cíclica con elementos
![]() , la primera diagonal cíclica con elementos
, la primera diagonal cíclica con elementos ![]() , etc. por
lo tanto es un tipo de matriz llamada circulante, además se cumple
que
, etc. por
lo tanto es un tipo de matriz llamada circulante, además se cumple
que ![]() , que es impuesto por las condiciones mecánicas de
las redes.
, que es impuesto por las condiciones mecánicas de
las redes.
Como vemos la matriz de movimiento ![]() es simétrica, que es
una consecuencia del problema pero que no va a influir mucho en las
consideraciones matemáticas.
es simétrica, que es
una consecuencia del problema pero que no va a influir mucho en las
consideraciones matemáticas.
Además es fácil ver que la matriz ![]() se puede
factorizar en la forma:
se puede
factorizar en la forma:
![\begin{displaymath}
M_c =\left[\begin{array}{lcl} a_0 & & 0 \\ & \ddots & \\ 0 ...
... 0 \\ & \ddots & \\ 0 & & a_1 \end{array}\right] II+
\cdots
\end{displaymath}](img623.gif)
![\begin{displaymath}
S = \left[\begin{array}{ccccc}
0 & 1 & & & \\
& & 1 & &...
...& \\
& & & \ddots & 1 \\
1 & & & & 0
\end{array}\right]
\end{displaymath}](img625.gif)
Por otra parte de las propiedades de esta matriz se sabe que:
Es decir tiene raices ![]() -ésimas de ``uno'' como eigenvalores
y los eigenvectores tienen la forma:
-ésimas de ``uno'' como eigenvalores
y los eigenvectores tienen la forma:
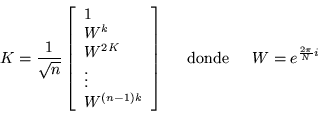
Por lo tanto con esta base, podemos solucionar el problema
cíclico que corresponde a un anillo; con estas consideraciones
podemos expresar la matriz ![]() en la forma:
en la forma:
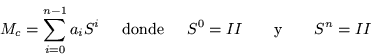 |
(5.2) |
Entonces las potencias se generan por un ciclo de ![]() 's, todas
diferentes, hasta
's, todas
diferentes, hasta ![]() que reproduce
que reproduce ![]() y
y ![]() ,...,etc.
,...,etc.
Además ![]() es una función de
es una función de ![]() , y cualquier función de
, y cualquier función de
![]() se puede escribir, utilizando un teorema visto con anterioridad en
la forma
se puede escribir, utilizando un teorema visto con anterioridad en
la forma
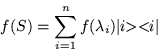 |
(5.3) |
 |
(5.4) |
Ahora sabemos que, ![]() está dada explícitamente
como una exponencial (ec. 5.1), que la matriz es simétrica,
lo cual nos permite determinar los eigenvalores de
está dada explícitamente
como una exponencial (ec. 5.1), que la matriz es simétrica,
lo cual nos permite determinar los eigenvalores de ![]() y que los
eigenvalores de una función matricial, son las mismas funciones de
los eigenvalores de la matriz original, entonces en lugar de la matriz
tenemos que sustituir los eigenvalores esto es:
y que los
eigenvalores de una función matricial, son las mismas funciones de
los eigenvalores de la matriz original, entonces en lugar de la matriz
tenemos que sustituir los eigenvalores esto es:
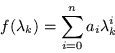
Además como
![]() que corresponde al eigenvalor
número
que corresponde al eigenvalor
número ![]() , tenemos
, tenemos
En donde ![]() es el entero más cercano y el último
término ocurre cuando
es el entero más cercano y el último
término ocurre cuando ![]() es par, por ejemplo si la matriz es
de orden 6 tenemos
es par, por ejemplo si la matriz es
de orden 6 tenemos
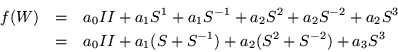
En donde vemos que sobra el término ![]() que corresponde
al último término de (5.5), además el exponente está
elevado a la dimensión de la matriz sobre dos; por lo tanto existe
una diferencia entre casos pares e impares que esta dado por el
último término.
que corresponde
al último término de (5.5), además el exponente está
elevado a la dimensión de la matriz sobre dos; por lo tanto existe
una diferencia entre casos pares e impares que esta dado por el
último término.
Calculemos:

![\begin{displaymath}
f(W^k) =a_0 II+2\sum_{i=1}^{n/2} a_i\cos\frac{2\pi }{N} ik +\frac{a_n}{2} [(-1)^k]
\end{displaymath}](img646.gif)
Que es la ley de dispersión, que da la frecuencia (al
cuadrado) como función del número de onda ![]() .
.
Para el caso de interacciones a segundos vecinos tenemos que
![]()
Expresando esta ecuación, con los mismos términos empleados
en el caso del interior de cualquier cadena, esto es:
Que es exactamente la relación de dispersión para el
interior de cualquier cadena, la única diferencia en la obtención
de esta ecuación con respecto a la primera, es que ésta tiene como
eigenvalores.