Comparación de los resultados con el interior de una cadena y conclusiones.

La gráfica de la relación (5.7) está dada por (IV.IV), en esa gráfica vemos que los eigenvalores caen sobre las líneas de ``$C$'' constante. Esto es porque el anillo necesita una condición de periodicidad, así que únicamene ciertos números de onda son permitidos (esto es, números de onda que corresponden a ondas oscilatorias). Además en este modelo vemos que habrán ciertas degeneraciones; donde las ondas de dos números de onda diferentes pueden tener las mismas frecuencias. En el plano $Z_1 -Z_2$ esos forman una red determinada por los ceros de los polinomios de Tchebychev esto es:

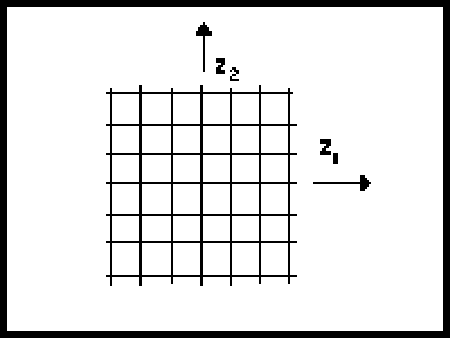
Además es necesario investigar si combinaciones lineales de esas ondas degeneradas tienden a desvanecerse sobre un par diametralmente opuesto de puntos.

Desde luego podemos escoger la fase de cada onda degenerada como se desee, podemos hacer que tengan un máximo entre las dos partículas nodales. Entonces por simetría, los desplazamientos de las dos partículas serán iguales.

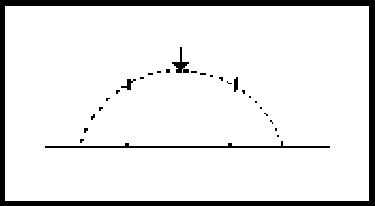
Para la otra onda degenerada haremos lo mismo, y por lo tanto ahora es un asunto sencillo encontrar los coeficientes para los cuales la suma se desvanece en ambos puntos.

En seguida hagamos la selección de tal forma de que los nodos caigan entre las partículas nodales. Esta vez las partículas tienen desplazamientos opuestos por simetría, esto es:

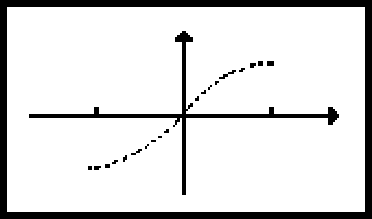
Una selección similar de fase para la segunda onda, permitirá otra vez una combinación lineal que se anule en las partículas nodales. Claramente esas dos construcciones, admiten modos normales independientes y por lo tanto tenemos una variedad bidimensional de ondas degeneradas, que se anulan en las partículas nodales, para el puro anillo tendremos una variedad tetradimensional, desde luego no exise restricción sobre la fase de una onda ni de su relación de amplitudes.

Una forma de comprobar lo anterior se puede ver analizando la relación de dispersión para un anillo, esto es, ecuación (5.5'), que nos da eigenvalores de $M_c$ expresadas por una serie de cosenos, por otra parte este es un caso de interés, ya que una matriz simétrica debe tener eigenvalores reales y los obtenidos aquí son complejos, pero esta ambiguedad se anula por un análisis gráfico del coseno que resulta en (5.5'), esto es, vamos a obtener $f(w^k)$, como está dado en función de una suma tenemos que dividir el intervalo entre $0$ y $2\pi$ y éste dividirlo en intervalos; de tal forma que si $i=1$ entonces $k=0,1,2,\ldots ,$ se encuentre en el intervalo $0\leq k\leq N$, lo cual quiere decir que el coseno dado por (5.5'), se encuentra entre $0$ y $2\pi$ al menos cuando $i=1$, por lo tanto la gráfica del coseno tendrá la forma siguiente:

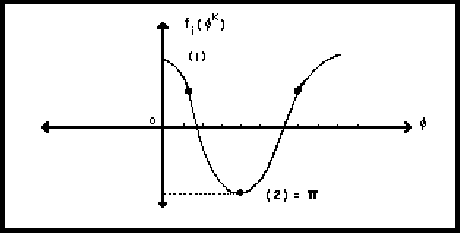
En donde hemos evaluado su argumento definido como $\theta =\frac{2\pi i}{N}k$ por lo tanto hay que ver en cada uno de los puntos, el valor de esta función, lo importante es que, como este subintervalo lo hemos dividido en una manera simétrica regular, entonces para cada valor de un lado tenemos su correspondiente simétrico en el otro lado, lo cual quiere decir que para $k$ y $n-k$ la función siempre toma el mismo valor, por lo tanto tenemos que el coseno tiene una simetría por reflexión respecto a $\pi$, entonces esto nos permite suponer que

$$f(W^k) =f(W^{-k})$$

Ya que es posible suponer que $-k =n-k$, entonces casi siempre existe una degeneración doble, y no existirá degeneración doble cuando $n$ es impar, en cuyo caso vemos el punto $\pi$ en un punto de subdivisión es decir vemos un sólo valor y esto corresponde el caso cuando se involucra el último término de la ecuación (5.5).

Otro caso es que excluimos los puntos $(1)$ y $(2)$ de la gráfica por lo tanto, los puntos donde el coseno alcanza a sus extremos que corresponden a $-1$ y $1$ no ocurren dobles, éstos corresponden al eigenvector de componentes $1$'s y al término $a_n /2$, porque en este caso tendremos valores de la forma $1,-1,1,-1,\ldots$ que ya son reales completamente, por lo tanto podemos formar combinaciones entre el vector $k$ y el $-k$, con lo cual podemos construir

$$K=\frac{1}{\sqrt{n}} \left[\begin{array}{l} 1 \\ W^k \\ W... ...W^{-k} \\ W^{-2k} \\ \vdots \\ W^{-(n-1)k} \end{array}\right]$$

Con esto podemos formar el vector siguiente:

$$\left[\begin{array}{c} \cos\frac{2\pi }{N}k . 0 \\ \cos\fr... .... 1 \\ \cos\frac{2\pi }{N}k . 2 \\ \vdots \end{array}\right]$$

En donde $0,1,\ldots$ son coordenadas espaciales, además podemos construir otro con componentes senos, también es posible construir uno con la parte imaginaria y otro con la real correspondiente al eigenvalor complejo.

Por lo tanto este es un aspecto del problema de un anillo, en el cual siempre existe degeneración doble, con excepción de las dos frecuencias extremas.

Además podemos ver, que para el caso en que $n$ es más grande, se obtiene el mismo resultado, entonces no importa a que número de vecinos se este llevando a cabo las interacciones.

Por otra parte vamos a tener como eigenfunciones, funciones que dependen de las coordenadas espaciales: $0,1,2,\ldots ,$ y de una función trigonométrica. Entonces escribiendo esto en forma lineal, obtendremos que para el caso en que $k=1$ vemos una onda cosenosoidal y otra sensoidal; cuando $k=2$, obtendremos una onda con dos oscilaciones, pero siempre se conserva su amplitud y por lo tanto hay que identificar el punto $(1)$ con el $(2)$ de tal forma que el desplazamiento sinosoidal sea respecto a las frecuencias de los anillos. El hecho de que la frecuencia espacial se considere fija, quiere decir que es cosenosoidal con un multiplicador, entonces vemos ondas con frecuencia creciente hasta llegar al extremo de que la frecuencia es tan grande que las partículas siguientes tienen desplazamientos $1,-1,1,-1,\ldots ,$ etc., lo cual da lugar a una función sinosoidal discreta, ya que lo que vamos a evaluar son puntos discretos.

Entonces tenemos una ley de dispersión que nos relaciona el número de onda (esto es, $(-1)^k a_n /2$), con la frecuencia $(W^k)$, por lo tanto si producimos una perturbación en el anillo y analizamos la superposición de las ondas en el mismo, particularmente cuando está formado por muchas partículas, observaremos una distorción ya que todas las ondas no se van a mover con la misma velocidad, debido a que todas tienen el mismo número de onda, pero la frecuencia que les corresponde no es nada lineal ya que siempre se fija el número de onda, en una onda determinada, por estas exponenciales complejas.

Por otra parte una cosa importante que debemos analizar es, la condición mecánica, esto es, $a_0 = -2a_1 -2a_2$ con lo que veremos de nuevo que el coseno es siempre menor que uno, entonces $a_0$ es igual a menos todos los coeficientes, (es decir, los elementos de la matriz de movimiento ) más los coeficientes multiplicados por un número cuyo valor es menor que uno, por lo tanto siempre saldrán negativos estos eigenvalores, o sea las $a$'s sumadas, cada vez se verán menores y como $a_0$ es menos la suma de todas las $a$'s se cumple que

$$-2\sum_{i\neq 0} a_i \leq f(W^k) \leq 0$$

Que es el intervalo dentro del cual quedan las frecuencias.

En interacciones a primeros vecinos, la relación de disposición que resulta es un coseno desfasado, tal que sus máximos lleguen a cero, lo cual es responsable de la forma, de la distribución cosenosoidal o arcosenosoidal, que siempre tienen las frecuencias de un sistema finito discreto.

En interacciones a segundos vecinos existe una degeneración, en el límite cuando el espectro es continuo y dicha degeneración es cuádruple ya que en este caso la relación de dispersión tiene dos máximos y un mínimo.

Además el hecho que $f(W^k)\leq 0$ es también debido a que $a_0$ es muy negativo y las $a$'s no son muy positivas, esto es porque tenemos un sistema oscilatorio y el desplazamiento generalmente resulta de una fuerza aplicada en el sentido contrario, en lugar de una fuerza paralela, por lo tanto los eigenvalores tienen que ser negativos, de tal forma de que sus raíces cuadradas tengan que salir imaginarias, con lo cual se tendrán oscilaciones en lugar de funciones hiperbólicas.

El caso en que la frecuencia temporal es igual al número de onda, no tiene mucho sentido, ya que esto implicaría que habríamos usado unidades tales que la velocidad del sonido tendría el valor de ``$1$'', lo cual si se puede hacer, pero no es conveniente, ya que podemos cambiar $f(W^k)$, por cambio en la unidad de su distancia, o en su unidad de tiempo, aunque existen algunos parámetros que no es posible modificar fácilmente, en el caso de que todos resultaran iguales, las ondas se moverían sin distorción siempre conservarán su forma, además si ondas distintas se mueven con velocidades distintas, entonces habrá distorción, la cual depende de la que se mueva mas rápidamente. Además sin cambiar la linealidad o propiedades del medio, ciertas ondas se mueven más rápidamente que otras, por lo tanto una onda larga puede llegar antes de que lleguen las componentes de alta frecuencia ya que inicialmente se genera un pulso de un lado y en el transcurso del movimiento éste es modificado, por lo tanto el pulso incial al llegar al otro extremo cambia, entonces la evidencia que vamos a observar en un anillo, con interacciones a segundos vecinos, es una compresión del rango; una extensión del mismo depende del signo relativo que puedan tener las frecuencias.

Otro aspecto es que se pueden apreciar frecuencias dobles, es decir, frecuencias próximas, entonces fuera de la degeneración normal, existe esta degeneración, la cual hace que una onda pueda pasar en dos direcciones esto mismo sucede en una cadena libre como veremos posteriormente, exsite otra degeneración no muy usual, pero que puede suceder en configuraciones muy distintas, como por ejemplo en aquellas en las que el número de onda sea completamente distinto, en donde además pueden resultar las mismas frecuencias, esto tiene que ver con el hecho de que exista cooperación o antagonismo entre primeros y segundos vecinos. Por último es necesario mencionar, que si tenemos interacciones a más vecinos, obtendremos una ley de dispersión más complicada, pero lo interesante es que pueden encontrarse máximos y mínimos entre mayor sea el número de interacciones, lo cual quiere decir que habrá más aproximaciones degeneradas.