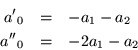Consideraciones del modelo, ecuaciones de movimiento.

Anteriormente vimos que es necesario aumentar elementos en las esquinas de la matriz de movimiento, de tal forma de poder emplearla uniformemente para el modelo con extremos fijos, lo cual es equivalente a prolongar la cadena suponiendo para ello, que existen dos partículas ficticias y que van a permanecer sin movimiento, aún cuando tengan el mismo tipo de interacción con las demás partículas que se encuentran en el interior de la cadena. Esto es semejante al caso de cuando se sostiene un hilo por sus extremos y no se deja mover, lo cual es conveniente por la uniformidad de la cadena, pero es poco real, ya que en las aplicaciones de sólidos es más conveniente suponer ``extremos libres'', de tal manera que los resortes extremos no existan, esto es:

$$k_0 =k_n =0$$

lo cual implicará un cambio en las constantes de las esquinas de la matriz $M$, esto es:

$$\left[\begin{array}{ccccccc} {a'}_0 & a_1 & a_2 & & & & \... ...''}_0 & a_1 \\ & & & & a_2 & a_1 & a_0 \end{array}\right]$$

En donde:

$$\begin{eqnarray*} {a'}_0 & = & -a_1 -a_2 \\ {a''}_0 & = & -2a_1 -a_2 \end{eqnarray*}$$

lo cual tiene validez si empleamos la condición mecánica, esto es $a_0 +2a_1 +2a_2 =0$, analizada con anterioridad.