Modos normales de vibración.

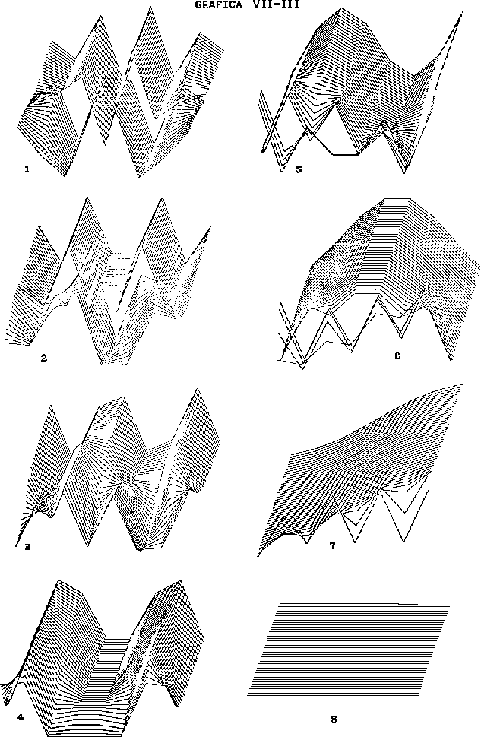
Para la descripción del comportamiento de estos modos normales, empleamos el mismo criterio que en el caso de la cadena de extremos fijos, tanto para la gráfica de frecuencias (Gráfica VII.II), como para la gráfica de los modos normales (Gráfica VII.III), pero se observaron diferentes propiedades, una de ellas es que no existen tantas degeneraciones como en el caso de extremos fijos, además que no se nota mucha discontinuidad cuando se cruzan dos curvas de frecuencia y la observación obvia de que el modo de frecuencia más baja no tiene nodos y en este caso corresponde a una traslación de las partículas, esto es debido al no confinamiento de las partículas extremas, el séptimo modo corresponde a una especie de rotación. En esta gráfica también tomemos como eje $-y$ en el espacio tridimensional, una perspectiva isométrica (correspondiente a un ángulo de $60^o$), en el eje $z$ a la razón de constantes de interacción y en el eje $x$ el número de partículas.