Modos Normales de vibración.

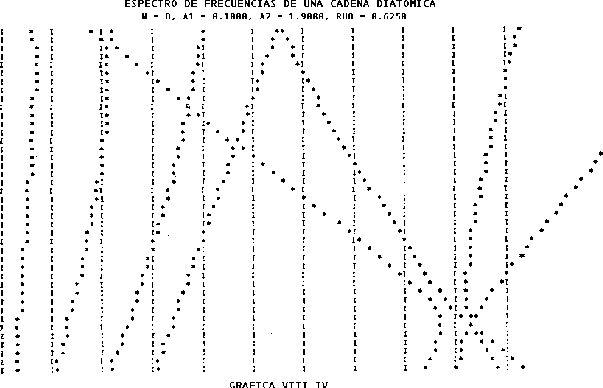
El espectro de frecuencias (Gráfica VIII.4) que nos marcará tendencias del comportamiento de los modos normales se realizó tomando como variable independiente la variación de frecuencias y como variable dependiente se tomó a $a_1$ como constante y $a_2$ de tal forma que $a_1 +a_2$ fuera constante, en esta misma forma se tomó el eje $z$ de los modos normales de vibración (gráfica VIII.5), el eje $-y$ como los desplazamientos, y el eje $x$ como el número de partículas; además se tomó un cociente de masas de 0.6250. En este caso se pueden apreciar regiones no definidas completamente como en el caso límite de primeros vecinos (banda acústica y óptica), estas regiones pueden traslaparse esto pasa cuando las interacciones a segundos son severas; además, si el número de onda es complejo puede dar lugar a un modo localizado que lo es en el sentido de que puede atravesar la región prohibida, si al menos uno es real indicará propagación. Un resultado interesante que se puede apreciar en el espectro de frecuencias es que en la rama óptica las curvas de frecuencia son rectas y que convergen en un punto (a este punto no se le ha podido dar una interpretación adecuada) de la misma forma que en los modos normales de vibración de modelos anteriores, podemos notar, que el modo de más baja frecuencia no tiene puntos nodales, de esto podemos decir que este modo es suceptible a todo tipo de variación.

Otra forma por la cual se puede ver las curvas definidas por la relación de dispersión es la siguiente.

Otra vez la relación de dispersión

$$\xi^2 +2P\xi(K+1) -2P\xi C +4C^2 -2C(K^2+4(K+1)) +2(K^2+4K+2) = 0$$

Que podemos poner en la siguiente forma

$$[\xi \;\;\; C]\left[\begin{array}{rr} 1 & -P \\ -P & 4 \end{a... ...d{array}\right] +2P\xi(K+1) -2C(K^2+4(K+1)) +2(K^2+4K+2) = 0$$

Calculando las raíces de la matriz de $2\times 2$

$$\begin{eqnarray*} \left\vert\begin{array}{cc} 1-\lambda & -P \\ -P & 4-\lambda ... ...y}\right\vert & = & 0 \\ (1-\lambda) (4-\lambda) -P^2 & = & 0 \end{eqnarray*}$$

Por lo tanto las raíces están dadas por

$$\lambda =\frac{5\pm \sqrt{25 +4(P^2-4)}}{2}$$

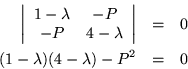
Con lo cual vemos que siempre tenemos una raíz positiva y una negativa.

Calculando las componentes de los eigenvectores tenemos

$$\left[\begin{array}{rr} 1 & -P \\ -P & 4 \end{array}\right]... ...t] =\lambda \left[\begin{array}{c} 1 \\ U \end{array}\right]$$

$$\begin{eqnarray*} 1 - P U =\lambda \\ U =\frac{1-\lambda}{P} \end{eqnarray*}$$

Por lo tanto la relación de dispersión define familia de hipérbolas.