Ahora deseamos encontrar los números de onda, lo cual se puede hacer
encontrando los eigenvalores ![]() de la matriz de transferencia.
de la matriz de transferencia.
![\begin{displaymath}
\left[\begin{array}{cccc}
K^2+\frac{\xi}{\rho}+2(K+1)-\mu...
...
1 & 0 & -\mu & 0 \\
0 & 1 & 0 & -\mu \end{array}\right] =0
\end{displaymath}](img786.gif)
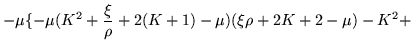 |
|||
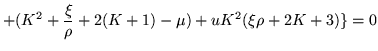 |
Reagrupando términos resulta la relación de dispersión que
involucra, ![]() y
y ![]() .
.
![$\displaystyle \mu^4 -\mu^3 [K^2 +\xi(\rho +\frac{1}{\rho}) +4(K+1)]
+\mu^2[(K^2 +\xi / \rho +2(K+1) )\cdot (\xi\rho +2(K+1))+$](img790.gif) |
|||
El coeficiente de ![]() puede ser simplificado más, para
esto, definimos
puede ser simplificado más, para
esto, definimos
![\begin{eqnarray*}
(X+\frac{\xi}{\rho})(X+\xi\rho) -2K^2 +2 & = & X^2 +X(\frac{\...
...4(K+1)^2 + [ 2(K+1)\xi(\frac{\rho +1}{\rho}) +\xi^2 - 2K^2 + 2 ]
\end{eqnarray*}](img793.gif)
Por lo tanto la relación de dispersión, conectando ![]() y
y
![]() es
es
Como vemos los coeficientes de esta ecuación resultan
simétricos, como en el caso del interior de una cadena. Además
sabemos que las raíces ocurren en parejas recíprocas,
definamos
| (8.13) |
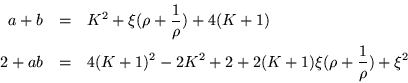
| (8.16) |
Estas ecuaciones determinan los números de onda como función
de ![]() y
y ![]() . Sin embargo, podemos resolver la relación de
dispersión para
. Sin embargo, podemos resolver la relación de
dispersión para ![]() , para esto despejamos
, para esto despejamos ![]() de la ecuación
(8.12) junto con la definición (8.15) resultando
de la ecuación
(8.12) junto con la definición (8.15) resultando
La ecuación ha sido simplificada al punto de que puede ser
solucionada para ![]() , esto es:
, esto es:
Que después de cierta álgebra toma la forma simplificada
Con objeto de checar el álgebra, consideremos el caso donde ![]() así que
así que
Ahora queremos solucionar para ![]() en términos de
en términos de ![]() y
y
![]() , por lo tanto reduciendo a una ecuación de segundo orden la
ecuación anterior.
, por lo tanto reduciendo a una ecuación de segundo orden la
ecuación anterior.
| (8.19) |
El descriminante, que define la transición entre números de
onda reales y complejos, es:
| (8.20) |
Para ![]() y
y ![]() fijos, hay dos valores de
fijos, hay dos valores de ![]() que satisfacen
esta relación, y para los cuales
que satisfacen
esta relación, y para los cuales ![]() puede tener una doble
raíz. Cuando
puede tener una doble
raíz. Cuando ![]() , hay solamente una raíz.
, hay solamente una raíz.
Para el caso general
| (8.21) |
Por lo tanto ![]() tendrá únicamente una raíz cuando
tendrá únicamente una raíz cuando
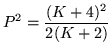 |
|||
| (8.22) | |||
Para valores de ![]() dados por la ecuación anterior, tendremos
la frontera entre la región real y compleja de los números de
onda, además es conveniente conocer donde
dados por la ecuación anterior, tendremos
la frontera entre la región real y compleja de los números de
onda, además es conveniente conocer donde ![]() , retornando a la
relación de dispersión dada por (8.17) y suponiendo
, retornando a la
relación de dispersión dada por (8.17) y suponiendo
![]() .
.
O sea que si ![]() entonces
entonces ![]() tendrá dos raíces
distintas y generalmente positivas, ya que el radical es siempre
positivo.
tendrá dos raíces
distintas y generalmente positivas, ya que el radical es siempre
positivo.
Modificando ligeramente la relación de dispersión (8.17)
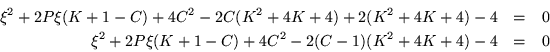
Lo que deseamos graficar es
![]() . En donde tenemos
que
. En donde tenemos
que ![]() es un parámetro que es la razón de masas y
es un parámetro que es la razón de masas y ![]() es una
constante que depende de los dos números de onda y que en las
gráficas es la que nos va a definir los contornos, con objeto de
distinguir las dos
es una
constante que depende de los dos números de onda y que en las
gráficas es la que nos va a definir los contornos, con objeto de
distinguir las dos ![]() 's que se obtienen una la denotamos con
's que se obtienen una la denotamos con ![]() y la
otra con
y la
otra con ![]() .
.
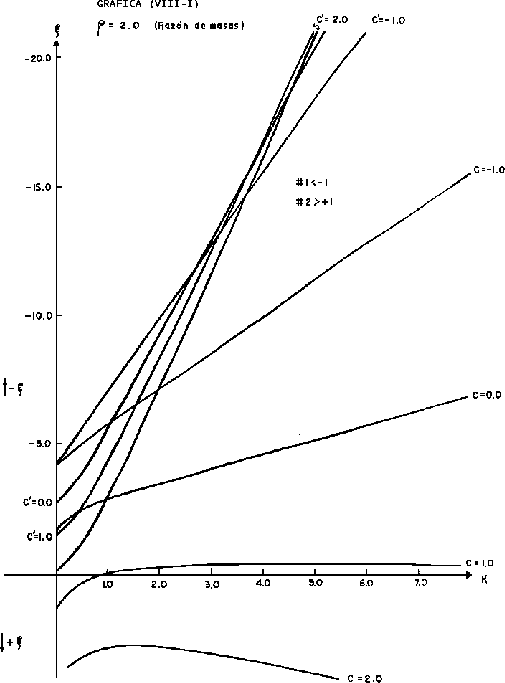
En la gráfica (VIII.1) la razón de masas ![]() que
utilizamos fué de 2:1, en esta gráfica podemos apreciar las bandas
características de las cadenas diatómicas, así podemos
distinguir la banda acústica (esta banda se caracteriza por curvas
de baja frecuencia) entre los contornos de
que
utilizamos fué de 2:1, en esta gráfica podemos apreciar las bandas
características de las cadenas diatómicas, así podemos
distinguir la banda acústica (esta banda se caracteriza por curvas
de baja frecuencia) entre los contornos de ![]() y
y ![]() en esta
región también podemos apreciar que al menos existe una onda
oscilatoria la cual nos indica que hay propagación. La banda
óptica está dada por la familia de curvas de
en esta
región también podemos apreciar que al menos existe una onda
oscilatoria la cual nos indica que hay propagación. La banda
óptica está dada por la familia de curvas de ![]() , en esta
gráfica vemos que no es posible ordenar las frecuencias por el
número de onda que es característico de primeros vecinos, esto
es debido a que hay una cierta inversión de las frecuencias en esta
región. La banda prohibida formada entre estas dos regiones se
caracteriza porque no existe ninguna onda
, en esta
gráfica vemos que no es posible ordenar las frecuencias por el
número de onda que es característico de primeros vecinos, esto
es debido a que hay una cierta inversión de las frecuencias en esta
región. La banda prohibida formada entre estas dos regiones se
caracteriza porque no existe ninguna onda ![]() .
.
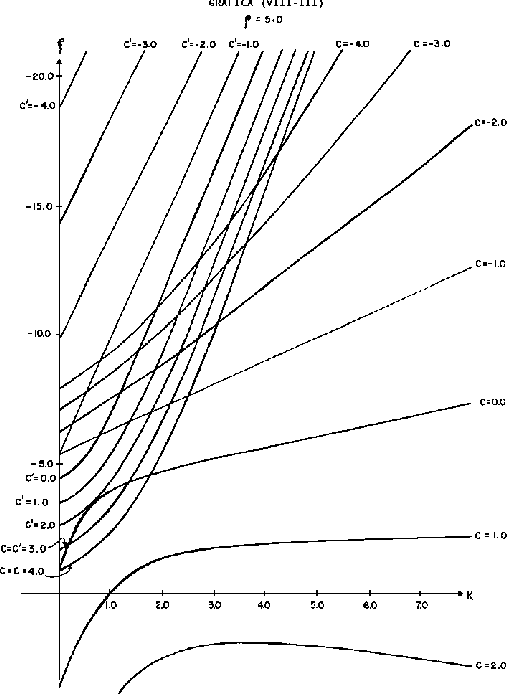
La gráfica (VIII.2) se llevó a cabo con una razón
de masas de ![]() lo cual nos indica que es el caso de la cadena
uniforme, al comparar esta gráfica con la (IV.IV) vemos que
concuerdan en algunos aspectos, otros aspectos que no son observados
con claridad debido a que se necesita una investigación mayor en
este punto, como por ejemplo no llevamos a cabo el análisis completo
de la región compleja que se caracteriza por estar formada por
familias de hipérbolas, sin embargo, el único fin que nos
propusimos fue el de indentificar ciertos aspectos que al final de
cuentas, fueran congruentes. La gráfica (VIII.3) es con
razón de más
lo cual nos indica que es el caso de la cadena
uniforme, al comparar esta gráfica con la (IV.IV) vemos que
concuerdan en algunos aspectos, otros aspectos que no son observados
con claridad debido a que se necesita una investigación mayor en
este punto, como por ejemplo no llevamos a cabo el análisis completo
de la región compleja que se caracteriza por estar formada por
familias de hipérbolas, sin embargo, el único fin que nos
propusimos fue el de indentificar ciertos aspectos que al final de
cuentas, fueran congruentes. La gráfica (VIII.3) es con
razón de más ![]() ésta da esencialmente la misma información
que la gráfica (VIII.2).
ésta da esencialmente la misma información
que la gráfica (VIII.2).
Una cosa que podemos apreciar de estas gráficas es que al aumentar la razón de masas, los rangos de las bandas se van haciendo más cortos.