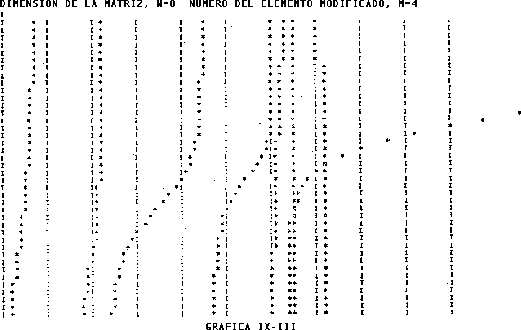
En este modelo, la gráfica del espectro de frecuencias (Gráfica
IX-III) se lleva a cabo tomando como eje vertical las
frecuencias y en el eje horizontal la variación del logaritmo del
cociente de masas, la variación fue de 2/8 a 8 con incrementos de
0.194, en la gráfica de los modos normales de vibración (Gráfica
IX-IV) tomamos como variable independiente (eje 
) la
variación del logaritmo del cociente de masas, en el eje y los
desplazamientos con perspectiva isométrica y el eje 
como el
número de partículas. En la serie de modos normales se puede
apreciar que si el defecto es ligero, el modo de frecuencia más
grande es localizado en el sentido de que tendrá una gran amplitud
de vibración en el sitio del defecto y decae exponencialmente lejos
del defecto. Este fenómeno es manifestado en el diagrama de
dispersión por notar que el punto que representa la frecuencia más
alta se mueve dentro de la región de números de ondas
pertenecientes a ondas amortiguadas a medida que la severidad del
defecto es aumentada. Si el defecto es pesado el modo de frecuencias
más bajo casi no se mueve, este modo se mueve jalando a todos los
demás, en el límite puden desaparecer dependiendo de la masa.
De la masa defectuosa dependerán los otros modos y que haya
cruzamiento.
