Modificación de dos Partículas Interiores.

Habiendo visto que la modificación de únicamente una masa en la cadena con interacciones a segundos vecinos no produce una ecuación secular que sea partículamente interesante, se puede confiar en la experiencia adquirida con una cadena con interacciones a primeros vecinos, entonces es permitido modificar una masa en el extremo de una cadena, sin embargo, en cadenas con interaciones a segundos vecinos, se requiere la modificación de dos átomos para cortar la cadena.

Analizando la matriz de recursión

$$\left[\begin{array}{cccc} \gamma & \beta & \gamma & -1 \\... ... 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]$$

El término que depende en la masa es $\beta$ a través de $\lambda m/K$. Por lo tanto el cambio de $m$ a $m(1+\delta)$ resulta en el cambio de $\beta$ a $\beta +\delta\lambda m/K =\beta+\epsilon$.

Si cambiamos las masas $i$ y $i+1$, tenemos entonces la modificación siguiente

$$\begin{eqnarray*} T_i \; \; \; \; \rightarrow & T_i +\left[\begin{array}{llll} ... ...0 & 0 & 0 & 0 \end{array}\right] & = \; T_{i+1} +\epsilon _1 \\ \end{eqnarray*}$$

y un segmento interior de los $T$ productos contiene:

$$(T_{i+1} +\epsilon _2)(T_i +\epsilon _1)=T_{i+1}T_i +\epsilon _2T_i +T_{i+1}\epsilon _i +\epsilon _2\epsilon _1$$

El último producto es cero, así que los términos dependiendo en $\epsilon$ son en forma matricial los siguientes:

$$\epsilon _2 \left[\begin{array}{llll} 0 & 1 & 0 & 0 \\ ... ... & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right]=$$

$$=\epsilon _2 \left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ ... ... 0 & 0 & 0 & 0 \end{array}\right] \qquad \qquad \qquad \qquad$$

Si llamamos la matriz total no modificada por $Q$, al segmento del lado izquierdo por $T$ y al segmento del lado derecho por $t$, resulta

$$\begin{eqnarray*} Q' & = & Q+ \left[\begin{array}{cccc} T_{11} & T_{12} & T_... ...lta \\ \Delta & \Delta & \Delta & \Delta \end{array}\right] \end{eqnarray*}$$

Por lo tanto el menor que determina la ecuación característica es

$$\left\vert\begin{array}{cc} Q_{11}+\epsilon _2 T_{11}t_{1... ...t_{22} +\epsilon _1 \gamma T_{21}t_{22} \end{array}\right]=0$$

Los dos límites significantes ocurren, por supuesto cuando $\epsilon \rightarrow 0$ y $\epsilon \rightarrow \infty$. Pero $\epsilon =0$, por supuesto que recuperamos la cadena sin modificar como se puede ver al hacer $\epsilon _1 =0$ y $\epsilon _2 =0$ en el determinante anterior. Para $\epsilon \rightarrow \infty$ podemos ignorar las $Q$'s, a menos cuando éstas no sean vitales para la obtención del determinante, esto es de su valor real.

Después de cierta álgebra resulta que la suma de las determinantes parciales para el caso en que $\epsilon \rightarrow \infty$ toma la forma

$$\begin{eqnarray*} & = & (\epsilon _2 t_{11} +\epsilon _1\gamma t_{21})(e_{11}t_... ...epsilon _1 t_{21} & \epsilon _1 t_{22} \end{array}\right\vert \end{eqnarray*}$$

Con lo cual resulta finalmente que la condición para obtener el espectro de eigenvalores cuando modificamos dos partículas en la cadena con interacciones a segundos vecinos es

$$Q_{11}^{\prime} =\epsilon _1 \epsilon _2 \left\vert\begin... ...t_{11} & t_{12} \\ t_{21} & t_{22} \end{array}\right\vert = 0$$

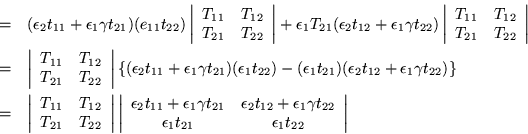
Por lo tanto en el límite, nuestro determinante se reduce a $\lambda^2$ veces el producto de los polinomios característicos para los dos segmentos dentro de los cuales la cadena se separa.