A ![]() matrix notation is admirably suited for discussing one-dimensional problems. For the Schrödinger equation, we would write
matrix notation is admirably suited for discussing one-dimensional problems. For the Schrödinger equation, we would write
| = | 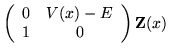 |
(1) |
For a constant potential it is a matter of finding the eigenvalues and eigenvectors of the coefficient matrix, then writing the solution as an exponential. Even so, there is a question of keeping the solution in a real form, making it convenient to distinguish V>E with a matrix of hyperbolic functions from the realm V<E with sines and cosines. After introducing the attenuation factor
| = | (V-E)1/2, | (2) |
| = | 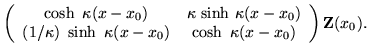 |
(3) |
| = | 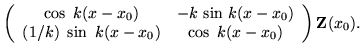 |
(4) |
Splitting a nominal period of ![]() into parts and multiplying the matrices corresponding to each part gives a result which could be graphed as a function of the parameters involved. Consider a one dimensional lattice whose base potential is zero, but for which part of the period consists of a barrier of height hi. In other words, the potential could be a Walsh function of simple form. The result of varying the height from the value of 0.0, representing a plane wave to 10.0, representing a sizable barrier, is shown in Figure 1. Actually it contains contour maps of the dispersion relation
into parts and multiplying the matrices corresponding to each part gives a result which could be graphed as a function of the parameters involved. Consider a one dimensional lattice whose base potential is zero, but for which part of the period consists of a barrier of height hi. In other words, the potential could be a Walsh function of simple form. The result of varying the height from the value of 0.0, representing a plane wave to 10.0, representing a sizable barrier, is shown in Figure 1. Actually it contains contour maps of the dispersion relation
| = | (5) |
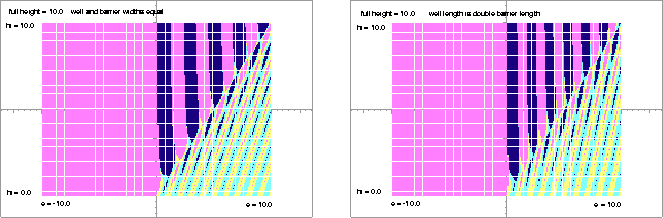 |
The expected result is that for energies larger than the barrier height, the solutions are mostly free waves, with occasuional exponential regions which can be attributed to Bragg reflection. On the other hand, for lower values of the energy the solution resembles bound states confined to the wells with a meagre possibility of tunneling between them, while the diffraction diminishes in intensity the further one goes above the top of the well.
Suppose that V is large with x-x0 proportionally small, keeping
![]() constant. Then
constant. Then
![]() would be infinitesimal with a huge
would be infinitesimal with a huge ![]() ,
whose reciprocal would remove the lower left element in the solution while cancelling the hyperbolic sine in the upper right element, finally leaving the factor P (remember that
,
whose reciprocal would remove the lower left element in the solution while cancelling the hyperbolic sine in the upper right element, finally leaving the factor P (remember that ![]() is only the square root of V). Altogether the solution matrix over such an interval is a shear:
is only the square root of V). Altogether the solution matrix over such an interval is a shear:
| = | 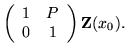 |
(6) |
Joined to an interval of length L, the resulting solution is
 | |||
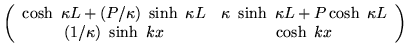 |
(7) | ||
The quantities of interest in this new matrix are still its eigenvectors and eigenvalues, and in particular whether the eigenvalues are hyperbolic or trigonometric. Half the trace of the matrix compared to unity tells which; we get
| = |  |
(8) |
Written with wave numbers to orient the interpretation towards free particles rather than bound states,
| = | 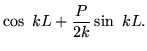 |
(9) |
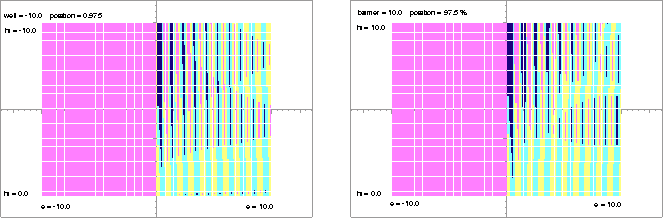 |
The dependence of the dispersion relation on P becomes evident when it is graphed. When P is zero, there is nothing but a plane wave, which is still mostly true when P is small. But when L corresponds to about half a free particle's wave length, there is an amplitude change resulting from a slight reflection, which is compounded as more and more unit cells are taken into account.
At the other extreme, a favorable phase relation allows consistent tunneling from one side of the potential step to the other, making a wave propagate. The size of P, which determines the scale of the effect, is measured by the same scale in which E or V themselves are expressed.
All these relationships can be discerned in Figure 2 on the left, in the regime of wells, interference creates narrow reflection bands wherein waves do not propagate. On the right in the regime of barriers, narrow tunneling bands permit wave propagation. The bands are not always so narrow, and are somewhat complementary, so the two figures look rather much the same. More resolution and enlarging the area under examination would be required to pursue the subject in greater detail.
If the contour maps are examined is closer detail, as in Figure 3, the ``bound state'' of the Kronig-Penney wells is visible. As the well becomes narrower, it has to become deeper to support a bound state, and thus will show up at an ever higher location in the contour plot as the delta-function limit is taken.
A third approach to the study of periodic potentials is to use a trigonometric function rather than a Walsh function for the potential of the Schrödinger equation. The solution involves the Mathieu functions, which have been well studied, but for which there are no limits which simplify the algebra as there were for the Kronig-Penney lattices.
Figure 4 shows the contour map for the Mathieu dispersion relation, otherwise known as its stability chart. The energy runs from -10.0 to 30.0, the amplitude of the cosine from 0.0 to 15.0. Here the potential is centered on zero, so there are negative energy bound states for sufficiently deep potentials. The Mathieu function itself is traditionally defined in terms of
![]() to give it a zero floor.
to give it a zero floor.
The program SERO calculates solutions for second order ordinary differential equationa or, equivalently, pairs of first order equations. The latter is the form already taken by the Dirac equation, so it is only necessary to write the coefficient matrix before proceding.
The program has a fixed list of potentials, with provision for varying some of their parameters. After they have been chosen, the solutions can be displayed in one or the other of two forms. One, the more traditional presentation, graphs solutions as functions of the independent variable, sometimes several at a time along with coefficients from the matrix in the form of options.
The other presentation is via the phase plane, wherein one component of the solution is plotted as a function of the other (often, its dertivative).
A sample of the two forms of presentation is shown in Figure 5. They are little used in this report, to get the illustrations for which an independent facility graphing selected dispersion relations has been used.