| = | 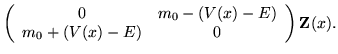 |
(10) |
The one-dimensional Dirac equation for a particle of rest mass m0 has a matrix form
| = | 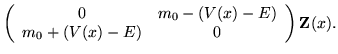 |
(10) |
The substitutions
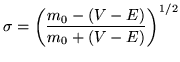 |
(11) |
| = | 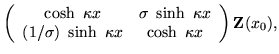 |
(12) |
When the rest mass is zero, the coefficient matrix is a scalar multiple of the unit antisymmetric matrix, so the use of the angle
Irrespective of either m0 or E, if V is very large yet extending over a small interval such that
![]() ,
the result is this same rotation matrix, now running through the angle P. An interesting consequence is that strengths differing by
,
the result is this same rotation matrix, now running through the angle P. An interesting consequence is that strengths differing by ![]() make identical changes to the solution.
make identical changes to the solution.
The fact that a concentrated potential produces a finite rotation rather than a shear is somewhat disconcerting, since it implies a discontinuity in both components of a solution vector. But mainly, this illustrates the fact that not all potentials give rise to continuous derivatives, nor even to continuous wave functions.
Following the Kronig-Penney precedent of compounding the delta-function potential with a plane wave, we would get
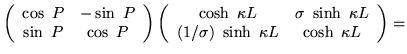 | |||
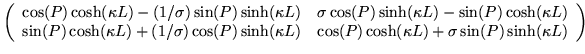 |
(15) | ||
| = | (16) |