Small mass compared to height

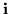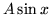When the mass is small or even zero, the coefficient matrix of the Dirac equation is nearly a scalar multiple of the unit antisymmetric matrix ${\bf i}$. Accordingly solutions take the form seen in Equations (13) and (13). For the potential $A\sin x$ the results for the interval 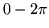$0 - 2\pi$ are

 

$$\varphi \int_0^{2\pi}(A\sin(t)-E)dt$$ =

$$[-A\cos(t) - Et]_0^{2\pi}$$ =

$$- 2\pi E$$ = (17)

and accordingly

 

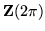$${\bf Z}(2\pi) \left(\begin{array}{cc} \cos(2\pi E) & -\sin(2\pi E) \\ \sin (2\pi E) & \cos\ (2\pi E) \end{array} \right) {\bf Z}(0),$$ = (18)

half of whose trace is 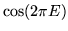$\cos(2\pi E)$, independently of the strength of the potential, and even of its form so long as it is periodic. This is evident in Figure 6 and even in the contour plot of Figure 7, whose apparent structure is more likely due to the precision of the computation than to the effects of mass, height, and energy.

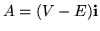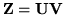Mass and energy may be separated in the Dirac equation by writing the coefficient matrix as M = A + B where $A = (V-E){\bf i}$ and $B=m_0{\bf j}$. Factoring the solution into ${\bf Z}= {\bf U}{\bf V}$ and solving

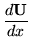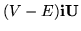$$\frac{d{\bf U}}{dx} (V-E){\bf i}{\bf U}$$ = (19)

to get the result already shown in Equation 18 (where the solution was called 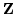${\bf Z}$), there remains the solution of the equation for ${\bf V}$,

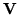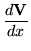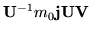$$\frac{d{\bf V}}{dx} {\bf U}^{-1}m_0{\bf j}{\bf U}{\bf V}$$ = (20)

When m₀ is small, it is approximately solved by the so-called first Born approximation

$${\bf V}(x) {\bf I}+ m_0\int_0^x {\bf U}(t)^{-1}{\bf j}{\bf U}(t) dt + \ldots$$ = (21)

$${\bf I}+ m_0\int_0^x {\bf j}{\bf U}^2(t) dt + \ldots,$$ = (22)

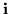the second form being due to the anticommutation of the quaternion matrices. Taking into account that ${\bf U}$ is a combination of ${\bf 1}$ and ${\bf i}$ while the integral is a mixture of ${\bf j}$ and ${\bf k}$, changes in the dispersion relation due to a small mass will be of at least second order.

  

Figure 6: A perspective view of the stability function for the relativistic Mathieu potential. Mass = 0.125, nearly negligible. Strength = 1.0. The energy varies from 0.0 to 3.5, the height of the potential form 0.0 to 1.5. Negative energies give the same results as positive energies. The mass causes a slight expansion of the interval -1.0 - 1.0 occupied by the massless half trace, something visible in the change of coloring.

  

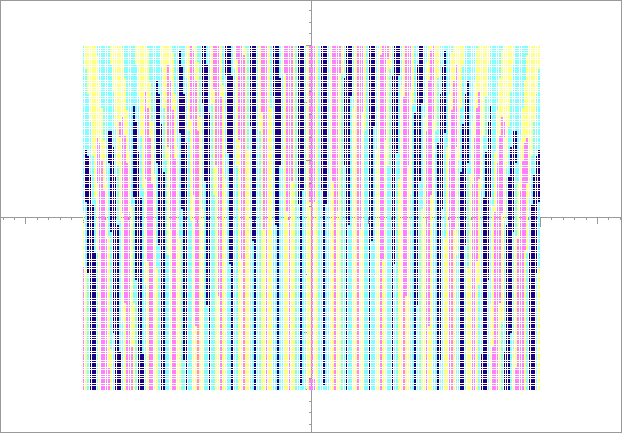
Figure 7: Stability contours for the relativistic Mathieu potential. There is essentially no variation with respect to the height of the potential, with results very close to those for a mass of exactly zero.