Ahora discutiremos otros espacios, de polinomios homogéneos de grado
mayor. Así hablaremos de ![]()
cuando ![]()
cuando ![]()
Definimos un monomio homogéneo de grado ![]() como el siguiente producto
como el siguiente producto
donde ![]() ,
, ![]() pueden ser elementos de
pueden ser elementos de
![]() ,
con la condición:
,
con la condición:
![]() es un espacio vectorial y trataremos de definir en él un producto
interno, utilizando el paréntesis de Poisson.
es un espacio vectorial y trataremos de definir en él un producto
interno, utilizando el paréntesis de Poisson.
Para esto nos fijamos en que si ![]() es un polinomio de
grado
es un polinomio de
grado ![]() y
y ![]() un polinomio de grado
un polinomio de grado ![]()
Entonces si escogemos ![]() tenemos
tenemos
Así repitiendo ![]() veces la misma operación,
veces la misma operación,
Hay que hacer notar que haciendo las operaciones con distintos
![]() el resultado sigue siendo un escalar.
el resultado sigue siendo un escalar.
En esta manera podemos definir funcionales lineales para los espacios
homogéneos de grado ![]() mayor que uno.
mayor que uno.
Si podemos definir un ![]() una funcional bilineal, utilizando los
paréntesis de Poisson casi hemos definido un producto interno.
una funcional bilineal, utilizando los
paréntesis de Poisson casi hemos definido un producto interno.
Supongamos que
![]() representa una funcional bilineal operando
sobre
representa una funcional bilineal operando
sobre ![]() por lo tanto tiene la forma
por lo tanto tiene la forma
donde
![]() pertenecen a
pertenecen a ![]() o
o
![]() es una combinación lineal de monomios homogéneos.
Así
es una combinación lineal de monomios homogéneos.
Así
será una combinación lineal de elementos de la forma
![]() donde por
donde por ![]() hemos denotado al
hemos denotado al ![]() -ésimo
monomio homogéneo que forma a
-ésimo
monomio homogéneo que forma a ![]() . Pero recordemos que
. Pero recordemos que ![]() es un
producto de polinomios homogéneos de grado uno.
es un
producto de polinomios homogéneos de grado uno.
Por lo tanto
![\begin{eqnarray*}
\left[{\varphi^\prime}^k,\varphi^k\right] & = &
\sum c_i \lef...
...ft[\prod_{i=1}^n q_i^{\alpha_i}p_i^{\beta_i},\varphi^k
\right]
\end{eqnarray*}](img509.gif)
Por lo tanto basta con definir la funcional para los monomios.
Queremos que:
Si ![]()
![\begin{eqnarray*}
\left\{x,\left\{y,uv\right\}\right\} & = &
- \left\{y,\left...
...\left\{y,\left\{x,uv\right\}\right\} \, = \, \left[yx,uv\right]
\end{eqnarray*}](img522.gif)
Con esta funcional bilineal definiremos la operación de conjugar canónicamente.
Con objeto de ilustrar la definición lo haremos primero en ![]() .
.
Recordemos que una funcional bilineal siempre define una funcional lineal.
Así definiremos una transformación lineal
![]() de la siguiente manera:
de la siguiente manera:
Tomemos la base de ![]() formada por los productos de la base
formada por los productos de la base
![]() , es decir;
, es decir;
Definimos el conjugado canónico de cualquiera de estos elementos
![]() como el elemento
como el elemento ![]() de la base tal que
de la base tal que
Averiguaremos ahora cuales son los conjugados de los distintos elementos.
Para esto veamos que si ![]() ,
, ![]() son dos monomios homogéneos de segundo
grado
son dos monomios homogéneos de segundo
grado
![\begin{eqnarray*}
\left[fg,uv\right] & = & \left\{f,\left\{g,uv\right\}\right\}...
...t\{g,v\right\}\right\} +
\left\{f,\left\{g,u\right\}v\right\}
\end{eqnarray*}](img533.gif)
Pero
![]() y
y
![]() son escalares, entonces
son escalares, entonces
Si consideramos ahora los elementos base de ![]() tenemos
tenemos
![\begin{eqnarray*}
T_{x_ix_j}(x_kx_l) & = & \left[x_ix_j,x_kx_l\right] \\
& = ...
...j,x_l \right\}+
\left\{x_i,x_l\right\}\left\{x_j,x_k \right\}
\end{eqnarray*}](img538.gif)
Definiendo
![]()
Consideremos ![]() entonces
entonces

Si ![]() obtendremos 0, en cambio si
obtendremos 0, en cambio si ![]()
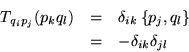
Así tenemos:
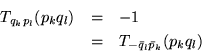
Esto nos induce a probar con el producto de los conjugados en el subíndice.
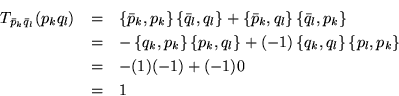
Ahora veamos los elementos de la forma ![]()
Para ![]() obtenemos:
obtenemos:
Hasta el momento hemos asumido ![]() , ¿Qué pasa si
, ¿Qué pasa si ![]() ?
?
Tomemos ![]()
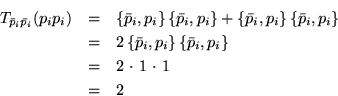
Para ![]() , también se obtiene lo mismo.
, también se obtiene lo mismo.
De aquí podemos ver que salvo para los elementos de la forma ![]() ya tenemos los elementos de la base dual, Pero si escogemos como base
de
ya tenemos los elementos de la base dual, Pero si escogemos como base
de ![]()
Después definimos por extensión lineal, exactamente de la misma manera
que en ![]() , el conjugado canónico de cualquier elemento de
, el conjugado canónico de cualquier elemento de ![]() .
.
Hay que notar que aquí la diferencia de ![]() , el conjugar
canónicamente es una operación involutoria y no anti-involutoria.
, el conjugar
canónicamente es una operación involutoria y no anti-involutoria.
En una manera similar podemos demostrar que para ![]() la funcional
la funcional
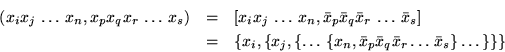
y la conjugación estará definida por
Habiendo visto como los paréntesis de Poisson pueden ser usados para
definir un producto interno, una operación de conjugación y un sistema de
bases duales tanto en el espacio fase ![]() como en los espacios de mayor
orden, de polinomios homogéneos
como en los espacios de mayor
orden, de polinomios homogéneos ![]() .
.
Ahora veremos como pueden ser usados para definir un espacio de
transformaciones lineales, las cuales actuarán sobre los espacios arriba
mencionados, estas transformaciones serán definidas por medio del espacio
de polinomios homogenéos de segundo grado ![]() .
.