Lema.- Si
Ahora probaremos que dada una base canónica, podremos construir una nueva base canónica, es decir, una base que tiene la propiedad de que si un vector pertenece a ella, su conjugado también pertenece a ella. Pero esta nueva base canónica la construiremos de tal manera que si un vector arbitrario distinto de cero queremos que esté en la base esto será posible.
Lo que haremos es contruir una nueva base canónica a partir de un vector arbitrario distinto de cero.
En realidad no tendremos mucha libertad en escoger los demás vectores base, pero cualquier vector que sea una combinación de coordenadas y momenta pueda llegar a ser un elemento base.
Primero probaremos el siguiente lema:
Lema.- Si
![]() , entonces
, entonces ![]() .
.
Corolario.- El único vector autoconjugado es el cero.
Lema - ![]() es ortogonal a
es ortogonal a ![]() .
.
Ahora sí, ya estamos en la posibilidad de construir nuestra nueva base.
Sea
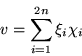
Así tenemos escrito ![]() como una combinación de
como una combinación de ![]() y
y
![]() con
con ![]() . Por tanto
. Por tanto
Ahora podemos escribir ![]() con respecto a esta base
con respecto a esta base
Sabemos que
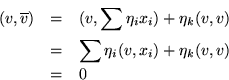
Pero
Así
Así podemos formar una nueva base
El unico problema que tenemos es que la base ![]() puede no ser ortogonal.
Pero el proceso de Gram-Schmidt puede verse que preserva el hecho de tener
solamente parejas conjugadas en la base.
puede no ser ortogonal.
Pero el proceso de Gram-Schmidt puede verse que preserva el hecho de tener
solamente parejas conjugadas en la base.
Realmente este último teorema puede generalizarse, y queda así:
Dada una base arbitraria, y un vector arbitrario siempre podemos construir una nueva base tal que el vector este en ella y consista de puras parejas de vectores conjugados canónicamente.
Sea
![]() la base y
la base y ![]() el vector.
el vector.
Formamos el conjunto

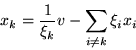
El conjunto
es linealmente independiente ya que si formamos
entonces
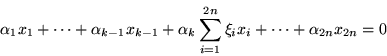
y como ![]() es linealmente independiente, entonces
es linealmente independiente, entonces
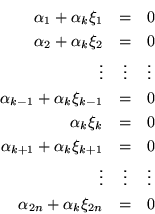
pero
Así tenemos una nueva base con nuestro vector formando parte de ella.
Ahora
Si todo ![]() es igual a cero tenemos contradicción, por lo tanto tenemos
uno de ellos, digamos
es igual a cero tenemos contradicción, por lo tanto tenemos
uno de ellos, digamos ![]() , distinto de cero.
, distinto de cero.
Aplicando el razonamiento anterior podemos tomar el conjunto
linealmente independiente.
Ahora tomamos cualquier ![]() tal que
tal que
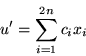

Formamos el conjunto
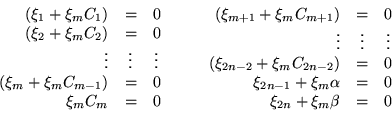
Lo que tenemos que hacer ahora es introducir ![]() en nuestra base,
para eso nos fijamos en que
en nuestra base,
para eso nos fijamos en que
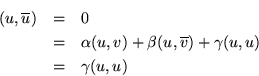
entonces
![]() .
.
Por tanto
![]() .
.
Así al menos uno de los coeficientes
Así tenemos que existe ![]() tal que
tal que ![]() es distinto de cero, quitando
este vector de la base y poniendo en su lugar
es distinto de cero, quitando
este vector de la base y poniendo en su lugar ![]() tendremos una nueva base
tendremos una nueva base
Este es un proceso finito, al término del cual tendremos una base conjugada y ortogonal. Lo cual prueba nuestro teorema.
Una pregunta natural que uno se hace, es si podemos formar una base con puros vectores que tengan la propiedad de que ninguno sea el conjugado de algún otro elemento de la base.
Para contestarla probaremos el siguiente:
Teorema.- La mayor sub-base ortogonal de nuestro espacio que no contenga un
conjugado cuenta con ![]() elementos, es decir, con la mitad de los elementos
que forman una base para el espacio.
Una sub-base de este tipo se llama isotrópica.
elementos, es decir, con la mitad de los elementos
que forman una base para el espacio.
Una sub-base de este tipo se llama isotrópica.
Lema 1.-
Demostración
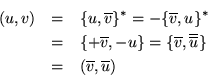
Lema 2.-
Si
entonces
Demostración
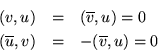
entonces falta ver el valor de
pero
Demostración del teorema.
Si tenemos una base isotrópica ortogonal tal que
entonces
y
ya que
por la definición de conjugado canónico.
Así por el lema 2
Pero debe ser ![]() por lo tanto
por lo tanto ![]() .
Así queda probado nuestro teorema.
.
Así queda probado nuestro teorema.
¿Que sucederia si en nuestro teorema acabado de probar quitamos la condición de ortogonalidad?
La respuesta a esta pregunta es que el teorema sigue siendo válido.
En resumen si denotamos por
![]() el conjunto de vectores los
cuales son conjugados de los vectores que pertenecen a un subespacio
el conjunto de vectores los
cuales son conjugados de los vectores que pertenecen a un subespacio
![]() , y si por
, y si por ![]() denotamos al conjunto de todos los paréntesis
de Poisson de la forma
denotamos al conjunto de todos los paréntesis
de Poisson de la forma ![]() tal que
tal que ![]() pertenezca a
pertenezca a ![]() y
y ![]() pertenezca a
pertenezca a ![]() . Entonces hemos visto que si
. Entonces hemos visto que si
Como una consecuencia de esto cuando deseamos encontrar un subespacio para
el cual
Por lo tanto un subespacio maximal isotrópico tiene dimensión ![]() y
y