$\Phi _n^{(2)}$ operando sobre $\Phi _n^{(k)}$

Tomaremos el conjunto de transformaciones lineales del espacio fase, conoceremos condiciones sobre sus eigenvalores y eigenvectores, definiremos el transpuesto de un operador y en base a esto el concepto de normalidad. En el caso del grupo simplectico, veremos que la matriz que representa a un vector autoadjunto tiene sus eigenvalores en parejas negativas. Esta es la propiedad que sustituye a la que tienen los operadores hermiteanos de que sus eigenvalores son reales.

El que los eigenvalores se agrupen en parejas negativas implicará que los respectivos eigenvectores, se agrupen en parejas conjugadas canónicamente.

Empecemos por hacer notar que si $f$ pertenece a $\Phi _n^{(k)}$ y $g$ pertenece a $\Phi_n^{(l)}$ entonces $\left\{f,g\right\} \in \Phi_n^{(k+l-2)}$.

Así

$$\left\{\Phi_n^{(k)},\Phi_n^{(l)}\right\}\subset\Phi_n^{(k+l-2)}$$

Ponemos una sola contención, porque no es posible decir que cada elemento de $\Phi ^{(k+l-2)}$ pueda ser representado como el paréntesis de Poisson de un elemento de $\Phi^{(k)}$ y uno de $\Phi^{(l)}$.

En el caso en que $k=2$ tenemos

$$\left\{\Phi_n^{(2)},\Phi_n^{(l)}\right\}\subset\Phi_n^{(l)}$$

es decir, el paréntesis de Poisson de un polinomio de $\Phi _n^{(2)}$ y uno de $\Phi_n^{(l)}$ nos dá nuevamente un polinomio de $\Phi_n^{(l)}$.

Cuando $k=l=1$

$$\left\{\Phi_n^1,\Phi_n^1\right\}\subset\Phi_n^0$$

que fué el caso con que empezamos nuestro trabajo, y hemos visto que esto nos llevó a encontrar las funciones lineales.

Por el momento prestaremos nuestra atención, al caso en que $l=1$. Así

$$\left\{\Phi_n^2,\Phi_n^1\right\}\subset\Phi_n^1$$

Sabemos que

$$\Phi^{(2)} = \left\{p_ip_j, p_iq_j, q_iq_j\right\}$$

y será un espacio vectorial que tiene $(2n+I)n$ productos, los cuales son una base.

Así en el caso de $\Phi_3^{(2)}$, su dimensión será 2I.

Debido a que $\Phi^{(2)}$ nos dá un mapeo de $\Phi^{(k)}$ en $\Phi^{(k)}$ por medio de paréntesis de Poisson, será conveniente nuevamente utilizar la notación

$$T_f(g) = \left\{f,g\right\}$$

donde $f$ es fijo y pertenece a $\Phi^{(2)}$ y $g$ es variable y pertenece a $\Phi^{(k)}$.

Los elementos matriciales de $T_f$ están dados por

$$(\,u,T_f(v)\,)=\left\{\bar{u},T_f(v)\right\}$$

donde $u$ y $v$ son elementos de la base de $\Phi^{(I)}$.

Ahora daremos la definición de la transpuesta de una transformación $T$, la cual denotaremos por $T^T$ y será;

$$\begin{array}{cccc} (T^T(g),h) & = & (g,T(h)) & \mbox{\hspace{.8in}}\forall g,h \in \Phi^1 \end{array}$$

Veremos si podemos averiguar algo más de $T^T$

$$(T^T_f(g),h)\stackrel{\rm def}{=} (g,T(h))=\left\{\bar{g},T_f(h)\right\}$$

por lo tanto en vista de que

$$T_f(h)=\left\{f,h\right\}$$

tenemos

$$(T_f(g),h)=\left\{\bar{g},\left\{f,h\right\}\right\}$$

pero la identidad de Jacobi nos dice que:

$$\left\{\bar{g},\left\{f,h\right\}\right\} + \left\{f,\left\... ...ght\}\right\} + \left\{h,\left\{\bar{g},f\right\}\right\} = 0$$

Recordando el hecho de que $g$ y $h$ pertenecen a $\Phi^{(1)}$ entonces

$$\left\{h,\bar{g}\right\} \in \Phi^0$$

por lo tanto

$$\left\{f,\left\{h,\bar{g}\right\}\right\} = 0$$

y así

$$\left\{\bar{g},\left\{f,h\right\}\right\} = - \left\{h,\left\{\bar{g},f\right\}\right\}$$

por lo tanto

$$\begin{eqnarray*} (T_f^T(g),h) & = & -\left\{h,\left\{\bar{g},f\right\}\right\}... ...,h\right\}\\ &=& \;\; (\overline{\left\{f,\bar{g}\right\}},h) \end{eqnarray*}$$

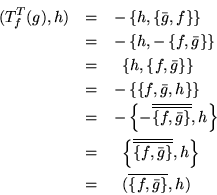
Así hemos encontrado que

$$(T_f^T(g),h) = (\overline{\left\{f,\bar{g}\right\}},h)$$

por lo tanto

$$T_f^T(g)=\overline{\left\{f,\bar{g}\right\}}=\overline{T_f(\bar{g})}$$

Entonces es posible tomar la definición de $T^T$ como :

$$T_f^T(u)=(\lambda(u)\overline{\left\{f,\bar{u}\right\}})=\overline{T_f(u)}$$

Recordando que cada elemento de $\Phi _n^{(2)}$ es un polinomio homogéneo de grado 2, lo cual significa que es una combinación lineal de productos de monomios, es decir, si $f$ pertenece a $\Phi _n^{(2)}$ entonces

$$f = \sum_{i\leq j}f_{ij} x_ix_j$$

y si tenemos una base ortonormal de $\Phi _n^{(2)}$, es decir,

$$(x_i,x_j) = \left\{\bar{x_i},x_j\right\}=\delta_{ij}$$

tendremos que

$$\begin{eqnarray*} T_f^T(x_k)& = & \overline{\left\{f,\bar{x}_k\right\}} \\ & ... ...\bar{x}_k\right\}^* + \bar{x}_j\left\{x_i,\bar{x}_k\right\}^*) \end{eqnarray*}$$

intercambiando el orden:

$$\begin{eqnarray*} T_f^T(x_i)& = & \sum_{i\leq j}f_{ij}^*(\bar{x}_i(-\left\{\b... ... & \left\{\sum_{i\leq j}-f_{ij}^*\bar{x}_i\bar{x}_j,x_k\right\} \end{eqnarray*}$$

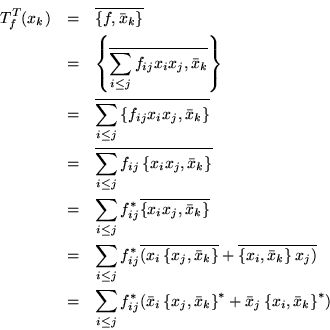
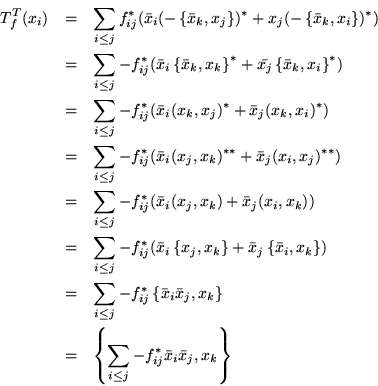
Si definimos, en términos de una base el conjugado de un elemento, $f$ de $\Phi _n^{(2)}$ como

$$\bar{f} = \sum_{i\leq j} -f_{ij}^*\bar{x}_i\bar{x}_j$$

donde $\bar{x_i}$ debe recordarse que es el conjugado de $x_i$, concepto que ya ha sido definido para elementos de $\Phi _n^{(1)}$.

En base a esta nueva definición tenemos:

$$\begin{eqnarray*} \left\{\sum -f_{ij}^*\bar{x}_i\bar{x}_j,x_k\right\} & = & \left\{\bar{f},x_k\right\} \end{eqnarray*}$$

Por tanto vemos que el transpuesto de $T$ puede ser definido también, por la siguiente expresión:

$$T_f^T(u)= \left( \lambda(u)\left\{\bar{f},u\right\}\right) =T_{\bar{f}}(u)$$