Sobre los eigenvectores

Un eigenvector de $T_f$ se define de la manera usual, un $u\neq0$ tal que

$$T_f(u) = \lambda u$$

donde $\lambda$ es un escalar.

Nótese que $T_f(u) = \lambda u$ es equivalente por definición a:

$$\left\{f,u\right\} = \lambda u$$

La determinación de tales eigenvectores, se reduce al hecho de diagonalizar la matriz $T_f$.

Si tomamos el conjugado canónico en ambos lados de la última igualdad.

$$\overline{\left\{f,u\right\}}=\overline{\lambda u}$$

tenemos que:

$$\overline{\left\{f,u\right\}}=\lambda^*\bar{u}$$

Pero como

$$T_f^T(u)=\overline{\left\{f,\bar{u}\right\}}$$

entonces

$$\begin{eqnarray*} \overline{\left\{f,u\right\}}&=&\overline{\left\{f,-\bar{\bar... ...rline{\left\{f,\bar{\bar{u}}\right\}} \\ & = & -T_f^T(\bar{u}) \end{eqnarray*}$$

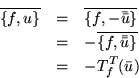
Así tenemos:

$$-T_f^T(\bar{u}) = \lambda^* \bar{u}$$

por lo tanto

$$T_f^T(\bar{u}) = -\lambda^* \bar{u}$$

o lo que es lo mismo

$$\left\{\bar{f},\bar{u}\right\}=-\lambda^* u$$

Lo que nos dice esta ecuación, es que si $u$ es un eigenvector de $T_f$ con eigenvalor $\lambda$, entonces $u$ es eigenvector de $T_f^T$ con eigenvalor $-\lambda^*$.

Así, si podemos determinar los eigenvalores y eigenvectores de un operador transpuesto, los del operador mismo serán conocidos.

Definimos un operador normal, de la manera usual, como aquel que conmuta con su transpuesto, donde, porque dos operadores $T_f$ y $T_g$ conmuten se entiende que:

$$T_f(T_g(u))=T_g(T_f(u)) \mbox{\hspace{.5in}} \forall u$$

es decir,

$$\left\{f,\left\{g,u\right\}\right\}= \left\{g,\left\{f,u\right\}\right\}$$

En vista de la identidad de Jacobi

$$\left\{f,\left\{g,u\right\}\right\} + \left\{g,\left\{u,f\right\}\right\} + \left\{u,\left\{f,g\right\}\right\} = 0$$

pero

$$\left\{g,\left\{f,u\right\}\right\} = \left\{g,-\left\{u,f\right\}\right\} = - \left\{g,\left\{u,f\right\}\right\}$$

por tanto

$$\left\{f,\left\{g,u\right\}\right\} = - \left\{g,\left\{u,f\right\}\right\}$$

sustituyendo en el identidad

$$- \left\{g,\left\{u,f\right\}\right\} + \left\{g,\left\{u,f\right\}\right\} + \left\{u,\left\{f,g\right\}\right\} = 0$$

entonces

$$\begin{eqnarray*} \left\{u\left\{f,g\right\}\right\} & = & 0 \\ \left\{\left\{f,g\right\},u\right\}& = & 0 \mbox{\hspace{.5in}}\forall u \end{eqnarray*}$$

Notemos que

$$\left\{f,g\right\} = h \in \Phi_n^{(2)}$$

y que nos está definiendo un operador $T_h(u)$.

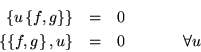
Así tenemos

$$T_h(u)=0\mbox{\hspace{.5in}}\forall u$$

Pero esto significa que

$$T_h \equiv 0$$

entonces

$$\left\{f,g\right\} = 0$$

Así la conmutatividad de dos operadores en $\Phi _n^{(2)}$, $T_f$, $T_g$ quiere decir que el paréntesis de Poisson de los elementos de $\Phi _n^{(2)}$ asociados a ellos sea cero, y esta es una condición necesaria y suficiente.

Entonces en el caso de un operador normal $T_N$, se satisface

$$\left\{\bar{N},N\right\} = 0$$

ya que

$$T_N^T = T_{\bar{N}}$$

Hasta el momento las últimas definiciones se han hecho sobre el espacio de operadores, ahora vamos a dar una definición sobre el espacio $\Phi _n^{(2)}$ mismo.

Así diremos que si $f$ pertenece a $\Phi _n^{(2)}$ es hermitiano

$$f = \bar{f}$$

Como corolario de la definición tenemos que el operador $T_f$, asociado con $f$ es normal. Como

$$T_fT_{\bar{f}}=T_{\bar{f}}T_f$$

porque

$$f = \bar{f}$$

y como

$$T_{\bar{f}}=T_f^T$$

entonces

$$T_fT_f^T=T_f^TT_f$$

El recíproco no siempre es cierto.

También diremos en el caso en que $f=\bar{f}$ con $f\in \Phi_n^{(2)}$ que $f$ es hermitiano.

Probaremos que los eigenvalores de un operador $T_f$, donde $f=\bar{f}$, aparecen en parejas conjugadas y lo son de vectores conjugados canónicamente con signos opuestos.

Sabemos que si

$$T_f(u) = \lambda u$$

entonces

$$T_f^T(u)= -\lambda^* u$$

o lo que es lo mismo

$$T_{\bar{f}}(\bar{u})= -\lambda^* \bar{u}$$

Pero $f=\bar{f}$, por tanto

$$T_f(\bar{u}) = -\lambda \bar{u}$$

Ahora estudiaremos la forma canónica de un operador normal.

Primero recordemos que la forma canónica de una matriz $M$ se entiende por

$$M = \sum_{i=1}^n x_i \,\vert\,i><i\,\vert$$

donde

$$\vert\,i><i\,\vert = G_i$$

son operadores idempotentes, es decir, tales que

$$G_i^2=G_i$$

y además son ortogonales, lo cual significa que

$$G_iG_j=0 \qquad \qquad i\neq j$$

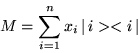
Trataremos de averiguar que forma toma el teorema espectral en el contexto en que estamos trabajando.

Si tomamos como hipótesis que existe un conjunto completo ortonormal de eigenvectores, entonces es posible escribir

$$f=\sum f_{ij}g_ig_j$$

ya que

$$f=\sum c_i \eta_i$$

en donde

$$\eta_j\in\Phi_n^{(2)}$$

es decir

$$\eta_i=\sum d_{jj^\prime}g_jg_{j^\prime}$$

con

$$g_j\in \Phi_n^{(1)}$$

por tanto

$$\begin{eqnarray*} f & = & \sum_{i=1}^n c_i \sum_{j,j^\prime=1}^nd_{jj^\prime}g_... ...\\ f & = & \sum_{j^\prime,j=1}^n f_{jj^\prime}g_ig_{j^\prime} \end{eqnarray*}$$

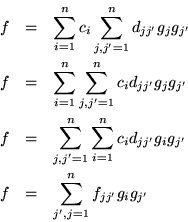
cambiando notación

$$f=\sum f_{ij}g_ig_j$$

Ahora apliquemos $f$ al producto $g_ig_j$ por medio de paréntesis de Poisson.

Notando que ahora la transformación definida por $f$ va de $\Phi _n^{(2)}$ en $\Phi _n^{(2)}$.

Recordando que $g_i$ y $g_j$ son eigenvectores de $f$

$$\begin{eqnarray*} \left\{f,g_ig_j\right\} & = & g_i(\lambda_jg_j) + (\lambda_... ..._jg_ig_j+\lambda_ig_ig_j \\ & = & (\lambda_i+\lambda_j)g_ig_j \end{eqnarray*}$$

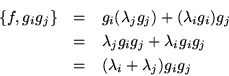
Lo cual nos está diciendo que si $g_i$ y $g_j$ son eigenvectores de $f$ su producto también lo es, y que va a tener como eigenvalor a la suma de los eigenvalores. Este resultado puede ser extendido a cualquier espacio $\Phi _n^{(k)}$ sobre el cual $f$ actue.

Así los eigenvectores de los elementos de $\Phi _n^{(2)}$, que operan sobre $\Phi _n^{(1)}$, dan eigenvectores en todos los demás espacios $\Phi_n^{(m)}$.

Es conveniente trabajar con una base $\left\{g_i\right\}$ que sea cerrada bajo la conjugación. Este es un resultado que siempre se tiene si $f$ es un operador normal.

De cualquier manera es posible formar una base, de eigenfunciones, canónicas. Esta base que es cerrada bajo conjugación puede ser numerada de la siguiente manera:

$$g_{-i} = \bar{g_i} \mbox{\hspace{.4in}} i>0 \mbox{\hspace{.4in}}(i=1,2......n)$$

Pero

$$(g_i,g_j) = \delta_{ij}$$

o en forma equivalente

$$\left\{\bar{g_i},g_j\right\} = \delta_{ij}$$

y por la convención de arriba

$$\left\{g_{-i},g_j\right\} = \delta_{ij} \mbox{\hspace{.8in}} i > 0$$

Para llevar a cabo esta ortonormalización, se sigue el proceso de ``Gram-Schmidt''. El proceso que hemos descrito para formar una base canónica.