Ahora demostraremos que para operadores normales y hermitianos sus eigenfunciones son ortogonales.
Sean ![]() y
y ![]() eigenfunciones de
eigenfunciones de ![]() , es decir,
, es decir,
Tomemos el producto interior de ![]() y
y ![]() .
.
Pero por otro lado
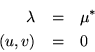
Es posible probar que los eigenvalores de un operador hermitiano son
reales
Pero ![]() , entonces
, entonces
Probaremos para un operador ![]() arbitrario que
arbitrario que
donde ![]() y
y ![]() son hermitianos, tomemos
son hermitianos, tomemos
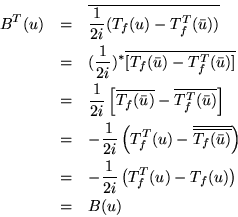
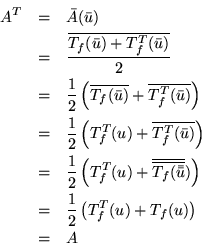
entonces
Ahora probaremos que ![]() es normal si y solo si sus partes real e
imaginaria conmutan.
es normal si y solo si sus partes real e
imaginaria conmutan.
Si ![]() es normal
es normal
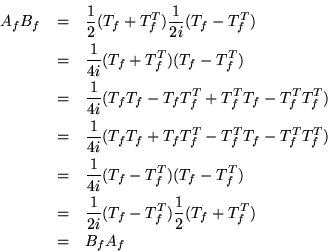
Ahora supongamos que ![]() , entonces probemos que
, entonces probemos que
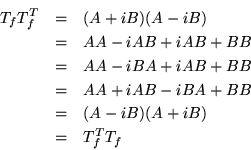
Ahora probaremos que si un operador es normal, entonces las eigenfunciones que pertenecen a eigenvalores distintos son ortogonales.
Consideremos.

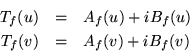
Como A, B y T conmutan es posible encontrar una base en la cual tienen los mismos eigenvectores, digamos
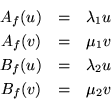
entonces
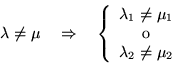
Si suponemos lo contrario a lo que queremos probar, o sea que
![]() y
y ![]() distintos pero
distintos pero ![]() y
y ![]() no son perpendiculares y
llegamos a una contradicción habremos probado nuestro teorema.
no son perpendiculares y
llegamos a una contradicción habremos probado nuestro teorema.
Como un corolario tenemos que las eigenfunciones, ![]() , de un operador
hermitiano forman una base canónica, es decir,
, de un operador
hermitiano forman una base canónica, es decir,
Tomemos la identidad de Jacobi:
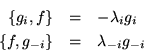

Los dos resultados más interesantes son que las eigenfunciones ocurren en parejas conjugadas canónicas y que los eigenvalores se presentan en parejas negativas.
Regresando a la función ![]() , sabemos que debe ocurrir
, sabemos que debe ocurrir
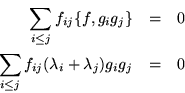
Ahora podemos escribir esto como
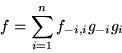
Supongamos que los eigenvalores son todos distintos.
Calculemos
![\begin{eqnarray*}
\{f,g_k\}& = &\lambda_{k}g_k \\
\sum_{i=1}^nf_{-i,i}\{g_{-i}...
...f_{-i,i}[g_{-i}\{g_i,g_k\}+\{g_{-i},g_k\}g_i]\ = \ \lambda_kg_k
\end{eqnarray*}](img718.gif)
cuando ![]() , no hay conclusión con respecto a
, no hay conclusión con respecto a ![]() y en caso contrario
vemos que
y en caso contrario
vemos que
Por tanto
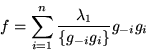
Aunque para llegar a este resultado hemos hecho la suposición de que los eigenvalores son distintos, esto fué hecho para ver el resultado con toda claridad y simplificar los cálculos. Ahora daremos la demostración en el caso general, es decir, que ahora admitiremos que haya degeneración.
Supongamos que hay eigenvalores iguales
entonces ![]() implica
implica
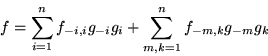
Pero
por lo tanto
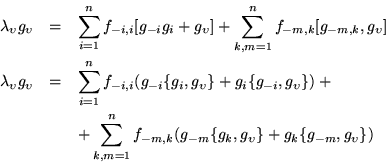
En el segundo sumando del término de la derecha debemos notar que
![]() , porque los términos que ocurren cuando
, porque los términos que ocurren cuando ![]() ya están
tomados en cuenta en el primer sumando.
ya están
tomados en cuenta en el primer sumando.
Y así obtenemos la misma relación que antes.