En este capítulo estudiaremos las transformaciones del tipo
Debido a los axiomas que cumplen, se tiene que ![]() es una
álgebra de Lie.
es una
álgebra de Lie.
El ser una álgebra de Lie implica muchas propiedades, no discutiremos todas, pero si aquellas que necesitemos aplicar.
Un álgebra de Lie cumple con:
![\begin{displaymath}
\begin{array}{cll}
\mbox{ (a) }& [f,g] = -[g,f] &\mbox{ant...
...,[h,f]]+[h,[f,g]] = 0 & \mbox{identidad de Jacobi}
\end{array}\end{displaymath}](img735.gif)
Como espacio vectorial,un álgebra de Lie puede tener dimensión finita o infinita, y en estos casos se habla de álgebras de Lie de dimensión finita ó infinita respectivamente.
Algunos tipos de estructuras algebraicas que son estudiados generalmente, se tienen dentro de esta teoría, por ejemplo:
Si ![]() es un álgebra de Lie y si
es un álgebra de Lie y si ![]() es un subconjunto de
es un subconjunto de ![]() ,
, ![]() ,
diremos que
,
diremos que ![]() es una subálgebra de
es una subálgebra de ![]() si
si ![]() mismo es un álgebra de Lie.
mismo es un álgebra de Lie.
Un criterio para verificar si un subconjunto ![]() es un álgebra, es que
es un álgebra, es que ![]() sea subespacio vectorial (es decir, cerrado respecto a combinaciones lineales
de elementos de
sea subespacio vectorial (es decir, cerrado respecto a combinaciones lineales
de elementos de ![]() ) y que
) y que
Ya que iia, iib y iic se cumplen para cualesquiera elementos de ![]() , por tanto
se cumplirán para los de
, por tanto
se cumplirán para los de ![]() .
.
Así para ![]() sólo hay que verificar la cerradura respecto a combinaciones
lineales y respecto a la conmutación.
sólo hay que verificar la cerradura respecto a combinaciones
lineales y respecto a la conmutación.
Existe otro tipo de subálgebra más restringida, en la cual se exige que se cumpla.
Así además de que ![]() es cerrado respecto a las combinaciones lineales, se
tiene que el conmutador, de un elemento de
es cerrado respecto a las combinaciones lineales, se
tiene que el conmutador, de un elemento de ![]() y cualquier elemento de
y cualquier elemento de ![]() , está en
, está en
![]() . En este caso el subespacio
. En este caso el subespacio ![]() se le llama un ideal. No existe ninguna diferencia
entre ideal izquierdo y derecho ya que
se le llama un ideal. No existe ninguna diferencia
entre ideal izquierdo y derecho ya que ![]() es
es ![]() pues solo hay un
cambio de signo y este no afecta el espacio vectorial. Por lo tanto cualquier
ideal izquierdo es ideal derecho. Debido a esto sólo se hablará de ideal.
pues solo hay un
cambio de signo y este no afecta el espacio vectorial. Por lo tanto cualquier
ideal izquierdo es ideal derecho. Debido a esto sólo se hablará de ideal.
De la definición se ve que ![]() es un ideal, lo mismo que
es un ideal, lo mismo que
![]() .
.
En el conjunto de ideales se puede definir una relación de orden, por medio de la inclusión de conjuntos.
Así diremos que el ideal ![]() es menor que el ideal
es menor que el ideal ![]() si
si
![]()
Si ![]() no es menor que
no es menor que ![]() ni
ni ![]() es menor que
es menor que ![]() , diremos que son
incomparables.
, diremos que son
incomparables.
En este sentido ![]() es el ideal máximo y
es el ideal máximo y
![]() es el ideal mínimo.
es el ideal mínimo.
La interseccion de dos ideales ![]() , es también un ideal, ya que la
intersección de espacios vectoriales es espacio vectorial y si
, es también un ideal, ya que la
intersección de espacios vectoriales es espacio vectorial y si
![]() entonces
entonces
Así vemos que la intersección es cerrada con respecto a la operación de
conmutación. Pero ![]() es el mayor conjunto contenido en
es el mayor conjunto contenido en ![]() y en
y en ![]() a la vez, por tanto será la mayor de las cotas inferiores.
a la vez, por tanto será la mayor de las cotas inferiores.
Tomemos dos subespacios ![]() y
y ![]() y definamos su suma,
y definamos su suma, ![]() , como el
conjunto de todas las combínaciones lineales finitas que podamos formar con
elementos de
, como el
conjunto de todas las combínaciones lineales finitas que podamos formar con
elementos de ![]() y de
y de ![]() .
.
Que ![]() es un subespacio vectorial se demuestra directamente de la
definición, lo que demostraremos en mayor detalle es que también es ideal.
es un subespacio vectorial se demuestra directamente de la
definición, lo que demostraremos en mayor detalle es que también es ideal.
Sea
![]()
donde
![]()
Sea ![]() Tomemos
Tomemos
Pero ![]() pertenece a
pertenece a ![]() o a
o a ![]() dependiendo en que
dependiendo en que ![]() sea un elemento
de
sea un elemento
de ![]() o un elemento de
o un elemento de ![]() por lo tanto
por lo tanto
Por tanto
Así
![]() es el menor subespacio que contiene a
es el menor subespacio que contiene a ![]() y a
y a ![]() , a la vez, como
subespacios, y siendo un ideal, también es el menor ideal que cumple con
esta propiedad.
, a la vez, como
subespacios, y siendo un ideal, también es el menor ideal que cumple con
esta propiedad.
Si recordamos la definicion de Red, vemos que los ideales de una álgebra, bajo el orden dado por la inclusión define una Red.
Veamos esto con un poco más de cuidado.
Una red está definida como un conjunto parcialmente ordenado en el cual, cada pareja de elementos tiene tanto una mínima cota superior como una máxima cota inferior.
Aquí tenemos que la mínima cota superior de ![]() y
y ![]() será
será ![]() y
la máxima cota inferior será
y
la máxima cota inferior será ![]() .
.
Un diagrama acerca de estas ideas siempre es de utilidad
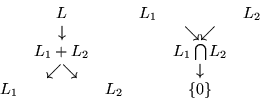
Una propiedad muy interesante acerca de estas álgebras es:
Esto es debido a que como ![]() y
y ![]() son ideales entonces
son ideales entonces
![\begin{eqnarray*}
\left[L_1,L_2\right] & \subset & L_1\\
\left[L_1,L_2\right] & \subset & L_2
\end{eqnarray*}](img766.gif)
Por lo tanto
No podemos afirmar que ![]() sea un espacio vectorial, esto es debido
a que la suma de dos conmutadores no es siempre otro conmutador, pero sabemos
del álgebra lineal que con cualquier subconjunto
sea un espacio vectorial, esto es debido
a que la suma de dos conmutadores no es siempre otro conmutador, pero sabemos
del álgebra lineal que con cualquier subconjunto ![]() de un espacio vectorial
podemos formar un espacio vectorial, este espacio es llamado el espacio
vectorial generado por
de un espacio vectorial
podemos formar un espacio vectorial, este espacio es llamado el espacio
vectorial generado por ![]() , la expansión lineal de
, la expansión lineal de ![]() ,
, ![]() ; también es
llamado la cáscara de
; también es
llamado la cáscara de ![]() y es denotado por
y es denotado por ![]() .
.
![]() es el conjunto de todas la combinaciones lineales finitas formadas
con elementos de
es el conjunto de todas la combinaciones lineales finitas formadas
con elementos de ![]() .
.
Ahora probaremos que
![]() es un ideal.
es un ideal.
Sea ![]() entonces
entonces
![\begin{displaymath}
x = \sum_{i=1}^k\alpha_i[l_1^i,l_2^i]
\qquad \mbox{ donde } \quad
l_1^i \in L_1
\; \mbox{ y }\;
l_2^i \in L_2
\end{displaymath}](img773.gif)
Probaremos que es una álgebra y de una vez que es un ideal si
Sea ![]()
Pero por la identidad de Jacobi
Pero
![\begin{eqnarray*}[l,x]& = & \sum\alpha_i \left(-[l_1^i,l_2^{i*}]-[l_2^i,l_1^{i*}...
... & \sum -\alpha_i [l_1^i,l_2^{i*}]+\sum\alpha_i [l_2^{i*},l_2^i]
\end{eqnarray*}](img783.gif)
De esta manera hemos verificado que ![]() es un ideal.
es un ideal.
Es fácil probar que ![]() es el mínimo ideal que contiene a
es el mínimo ideal que contiene a
![]() .
.
Ya que si ![]() es un ideal que contiene a
es un ideal que contiene a
![]() entonces cualquier elemento
entonces cualquier elemento
![]() será de la forma
será de la forma
![]() donde
donde
![]() por lo tanto
por lo tanto
Así ![]() contiene a la cáscara de
contiene a la cáscara de ![]()
Ahora veremos que si ![]() es una subálgebra, existe una subálgebra
es una subálgebra, existe una subálgebra
![]() , tal que
, tal que ![]() y
y ![]() será la mayor subálgebra en que
será la mayor subálgebra en que ![]() es un ideal.
En el caso en que
es un ideal.
En el caso en que ![]() es un ideal,
es un ideal, ![]() tendrá que coincidir con
tendrá que coincidir con ![]() . A la
subálgebra
. A la
subálgebra ![]() le llamaremos el normalizador de
le llamaremos el normalizador de ![]() .
.
Definimos ![]() como
como
Que es un subespacio vectorial lo vemos de que si ![]() ,
, ![]() entonces
entonces
![\begin{eqnarray*}
\mbox{$[\alpha x + \beta y,r]$} & = & \mbox{$[\alpha x ,r] + [\beta y,r]$}\\
& = & \mbox{$[x,\alpha r] + [y, \beta r] \in R$}
\end{eqnarray*}](img798.gif)
Ahora veremos que el normalizador es cerrado bajo la conmutación.
Sean ![]() y
y ![]() dos elementos arbitrarios de
dos elementos arbitrarios de ![]() , veremos que
, veremos que
Llamemos ![]() al conmutador de
al conmutador de ![]() y
y ![]() , es decir,
, es decir,
Ahora
Pero
Ya solo nos falta ver que ![]() es un ideal en
es un ideal en ![]() , es decir, que se cumple
, es decir, que se cumple
Pero esto es una consecuencia directa de la definición de normalizador.
Que ![]() es la mayor subálgebra en la que
es la mayor subálgebra en la que ![]() es normal, se obtiene de ver
que si
es normal, se obtiene de ver
que si ![]() es normal en
es normal en ![]() , entonces
, entonces ![]() lo cual implica que
lo cual implica que ![]() por lo tanto
por lo tanto ![]() .
.
En este punto vale la pena resumir los resultados que hemos obtenido:
Dados dos ideales ![]() y
y ![]() :
:
Además dado un subespacio ![]() de
de ![]() , existe un ideal
, existe un ideal ![]() que contiene
a
que contiene
a ![]() y es el más pequeño con esta propiedad. Y si
y es el más pequeño con esta propiedad. Y si ![]() es una subálgebra existe
una subálgebra máxima en al que
es una subálgebra existe
una subálgebra máxima en al que ![]() esta contenida como un ideal.
esta contenida como un ideal.
Esta subálgebra es llamada el normalizador de ![]() .
.
Ahora introduciremos dos conceptos algebraicos muy usados en teoría de grupos.
Dada una subálgebra ![]() es posible formar una cadena de subálgebras, tal
que esta, sea decreciente.
tomemos
es posible formar una cadena de subálgebras, tal
que esta, sea decreciente.
tomemos
![\begin{eqnarray*}
R\supset R^\prime & = & (([R,R]))\\
R^\prime \supset R^{''}...
... \\
R^{(k-1)}\supset R^{(k)} & = & (([R^{(k-1)},R^{(k-1)}]))
\end{eqnarray*}](img822.gif)
Esta cadena es llamada la serie derivada, y si después de un número finito
de términos obtenemos el idal ![]() , diremos que
, diremos que ![]() es soluble.
es soluble.
Es posible demostrar que ![]() es un ideal en
es un ideal en ![]() para toda
para toda ![]() .
.
Otra manera de definir una cadena decreciente de subálgebras es:
![\begin{eqnarray*}
L\supset L^2 & = & (([L,L]))\\
L^2\supset L^3 & = & (([L^2,...
...
\vdots & & \vdots \\
L^k\supset \L ^{k+1}& = & (([L^k,L]))
\end{eqnarray*}](img826.gif)
Si después de un número finito de términos obtenemos el ideal ![]() , diremos
que
, diremos
que ![]() es una subálgebra nilpotente.
es una subálgebra nilpotente.
Debido a que ![]() es un ideal soluble en cualquier álgebra de Lie,
tenemos que toda álgebra contiene ideales solubles.
es un ideal soluble en cualquier álgebra de Lie,
tenemos que toda álgebra contiene ideales solubles.
Por tanto tiene sentido hablar del máximo ideal soluble y a esto se le llama el radical.
Si el radical resulta ser el ![]() diremos que el álgebra es semisimple.
diremos que el álgebra es semisimple.
Ahora daremos la definición de álgebra simple, ésta será una cuyos
únicos ideales sean ella misma y ![]() .
.
A continuación mencionamos un teorema, cuya demostración está fuera de nuestro alcance, (para una demostración ver Jacobson [2]). La importancia del teorema radica en que nos permite restringir nuestra atención a las álgebras simples, pues las semisimples se estudiarán en función de aquellas. Ya que el teorema dice lo siguiente:
![]() es una álgebra semisimple si y solo si es la suma directa de ideales
que como álgebras de Lie son simples.
es una álgebra semisimple si y solo si es la suma directa de ideales
que como álgebras de Lie son simples.
Ahora daremos un ejemplo de álgebra de Lie el cual será de gran utilidad más adelante.
Consideremos el conjunto de matrices cuadradas de orden ![]() . Que las matrices
forman un álgebra de Lie facilmente se prueba si definimos
. Que las matrices
forman un álgebra de Lie facilmente se prueba si definimos
1.- Antisimetría
![\begin{eqnarray*}
\mbox{$[A,B]$} & = & AB - BA\\
& = & -BA + AB\\
& = & -(BA - AB)\\
& = & -\mbox{$[B,A]$}
\end{eqnarray*}](img828.gif)
2.- Linealidad
![\begin{eqnarray*}
\mbox{$[A,\alpha B+\beta C] $} & = & A(\alpha B+\beta C)-(\al...
...+\beta (AC - CA)\\
& = & \mbox{$\alpha [A,B] + \beta [A,C] $}
\end{eqnarray*}](img829.gif)
3.- Identidad de Jacobi
![\begin{eqnarray*}
\lefteqn{ [A,[B,C]]+[B,[C,A]]+[C,[A,B]] = }\\
& = &A[B,C]-[B...
...ABC)+(CBA-CBA)+(BCA-BCA)+(ACB-ACB)+(CAB-CAB)+(BAC-BAC)\\
& = &0
\end{eqnarray*}](img830.gif)
Los resultados algebraicos usuales tienen validez, es decir, la imagen y contraimagen de un ideal es un ideal.
La contraimagen del ![]() es el nucleo del homomorfismo y es un ideal.
es el nucleo del homomorfismo y es un ideal.