La teoría de las álgebras de Lie desarrolla, además de los conceptos enunciados en la sección anterior, una clasificación de las álgebras simples y la herramienta principal para llevar a cabo esta labor es la representación regular o representación adjunta.
Comenzamos por dar unas definiciones.
Por un homomorfismo entre dos álgebras ![]() y
y ![]() , entendemos una función
, entendemos una función
1)
![]() para toda
para toda ![]() y para todo
y para todo ![]() elementos de
elementos de ![]()
2)
![]()
donde por ![]() y
y ![]() entendemos las suma y la conmutación en
entendemos las suma y la conmutación en
![]() , con
, con ![]()
De ahora en adelante ya no usaremos los subíndices para diferenciar las operaciones de las distintas álgebras.
Si nosotros pedimos que el espacio ![]() sea un espacio de
transformaciones lineales, entonces diremos que
sea un espacio de
transformaciones lineales, entonces diremos que ![]() es una
representación de
es una
representación de ![]() .
.
Regresemos a la representación adjunta. Esta representación se basa en el hecho de que un álgebra de Lie es un espacio vectorial, y que la función
es un operador lineal para este espacio, y que por tanto puede ser representado por medio de una matriz, con respecto a una base dada. Estos conceptos los utilizaremos nosotros solo en el caso en que tengamos dimensión finita.
Así lo que tendremos será la representación del conmutador con un argumento fijo.
![]()
La figura de arriba nos dice que a un elemento ![]() del álgebra, le podemos
asociar un operador
del álgebra, le podemos
asociar un operador ![]() , y a este operador una matriz
, y a este operador una matriz ![]() , a final de cuentas
hemos asociado con cada elemento
, a final de cuentas
hemos asociado con cada elemento ![]() una matriz
una matriz ![]() .
.
Describiremos más detalladamente ahora lo que es la representación adjunta.
Si el álgebra de Lie tiene una base
![]() , es decir,
, es decir,
entonces para cada ![]()

Si aplicamos ![]() a
a ![]() , tendremos
, tendremos
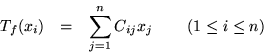
![\begin{eqnarray*}
T_f & \rightarrow & \left[
\begin{array}{cccc}
C_{11}& C_...
... \\
C_{n1}& C_{n2} & \cdots & C_{nn}
\end{array} \right] = F
\end{eqnarray*}](img846.gif)
La importancia de este representación, yace en el hecho de que cualquier álgebra de Lie puede ser ahora reemplazada por una álgebra, la cual es asociativa.
Hasta ahora hemos estado hablando de la representación adjunta y sin embargo todavía no hemos probado que en realidad tenemos un homomorfismo. Esto será lo que haremos a continuación.
Por ![]() representemos el mapeo tal que
representemos el mapeo tal que
y por ![]() el que hace que
el que hace que
Sean ![]() y
y ![]() dos elementos cualesquiera del álgebra de Lie, probaremos que
dos elementos cualesquiera del álgebra de Lie, probaremos que
Pero esto es cierto ya que hemos probado que ![]() es un isomorfismo que
preserva la suma, en la
es un isomorfismo que
preserva la suma, en la ![]() , y lo mismo se puede decir de
, y lo mismo se puede decir de ![]() (y la
demostración se puede ver en Halmos, Gelfand). Pero
(y la
demostración se puede ver en Halmos, Gelfand). Pero ![]() además preserva
la composición de transformaciones.
además preserva
la composición de transformaciones.
Así tenemos
ya nada más nos falta probar que
Tenemos que
Pero
Y por la identidad de Jacobi
![\begin{eqnarray*}
\mbox{$T_{[f,g]} (h)$} & = & \mbox{$ [f,[g,h]] - [g,[f,h]] $}...
... & T_f (T_g (h))-T_g (T_f (h))\\
& = & (T_f T_g - T_g T_f)(h)
\end{eqnarray*}](img856.gif)
por lo tanto
entonces ![]() es mapeado en
es mapeado en ![]()
Así
por tanto
![\begin{eqnarray*}
\varphi(\mbox{$[f,g]$}) & = & FG-GF\\
& = & \mbox{$ [F,G] $}\\
& = & \mbox{$ [\varphi(f),\varphi(g)] $}
\end{eqnarray*}](img861.gif)
Así vemos que ![]() preserva la conmutación y que con el conmutador de
preserva la conmutación y que con el conmutador de ![]() y
y ![]() tenemos asociado el conmutador de
tenemos asociado el conmutador de ![]() y
y ![]()
Habiendo notado que las matrices cuadradas forman un espacio vectorial, uno se pregunta si es posible hacerlo un espacio con producto interno.
En este espacio se tiene definida una forma bilineal
![]() llamada la forma de Killing, la cual está definida de la siguiente manera:
llamada la forma de Killing, la cual está definida de la siguiente manera:
En donde ![]() , denota la Traza de
, denota la Traza de ![]()
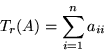
En el caso en que nuestras matrices están formadas por números reales
Los axiomas de producto interno

se pueden probar a partir de las dos siguientes propiedades de la traza de una matriz
y
Así que solo faltaría ver que
![\begin{eqnarray*}
X = \left[ \begin{array}{ccccc}
0 & 0 & \cdots & 0 & 1\\
0...
...ox{.}& \mbox{.}\\
0 & 0 & \cdots & 0 & 0
\end{array} \right]
\end{eqnarray*}](img871.gif)
Esto nos podría insinuar el abandonar la forma de Killing, pero resulta que su propiedad más importante tiene que ver con conmutadores, y esta es que
Esta igualdad se basa en el hecho de que
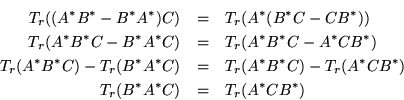
La demostración de este hecho se puede hacer facilmente de la siguiente
manera. Para ![]() basta con ver como se define el producto de matrices y la
definicion de traza, y después si tenemos
basta con ver como se define el producto de matrices y la
definicion de traza, y después si tenemos ![]() asociar
asociar ![]() aplicar lo probado para
aplicar lo probado para ![]() y vemos que su traza es la de
y vemos que su traza es la de ![]() .
.
El problema que tenemos ahora es hacer positiva esta forma cuadrática,
pero esto se logra si definimos
Se puede probar que ahora si ![]() es un producto interno.
es un producto interno.
De nuevo la relación entre la semimétrica definida por la forma de Killing y la métrica definida por este producto interno, nos lleva a la definición de conjugación, y al teorema de parejas en los eigenvalores que poseen estas matrices como operadores sobre el álgebra de Lie (Considerada como espacio vectorial).
Un eigenvector ![]() de
de ![]() satisface, dentro del álgebra de Lie,
satisface, dentro del álgebra de Lie, ![]() , la
siguiente ecuación:
, la
siguiente ecuación:
Si en la representación de ![]() el asociado de
el asociado de ![]() es
es ![]() y el de
y el de ![]() es la matriz
es la matriz
![]() , tendremos que bajo el homomorfismo que nos da la representación
, tendremos que bajo el homomorfismo que nos da la representación
Aquí podemos pedir la normalidad de ![]() para asegurarnos la existencia de un
conjunto completo ortonormal de eigenvectores, pues las matrices normales son
las únicas que cumplen con este requisito.
para asegurarnos la existencia de un
conjunto completo ortonormal de eigenvectores, pues las matrices normales son
las únicas que cumplen con este requisito.
Consideremos un eigenvector de ![]() , al cual llamaremos
, al cual llamaremos ![]() , para este se
cumple que
, para este se
cumple que
Pero de (12)
Por tanto tendremos que

De aquí vemos que si ![]() es un eigenvector de
es un eigenvector de ![]() con eigenvalor
con eigenvalor ![]() y si
y si
![]() es un eigenvector de
es un eigenvector de ![]() en
en ![]() , entonces o
, entonces o ![]() ó
ó ![]() es otro eigenvector
de
es otro eigenvector
de ![]() y cuyo eigenvalor es
y cuyo eigenvalor es
![]() .
.
Ahora consideremos
Si multiplicamos la ecuación (12), a la derecha, por ![]() tendremos
tendremos
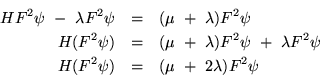
Si seguimos de esta manera, encontraremos una cadena de eigenvalores y eigenvectores.
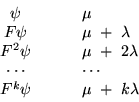
Como el eigenvalor de ![]() es diferente de todos los demás entonces
es diferente de todos los demás entonces ![]() debe ser cero puesto que de otra manera la matriz
debe ser cero puesto que de otra manera la matriz ![]() tendría otro eigenvector
linealmente independiente
tendría otro eigenvector
linealmente independiente
De esta manera vemos que si
![]() la única manera de que
termine la cadena es que
la única manera de que
termine la cadena es que ![]() . Hay que hacer notar que lo único
que sabemos es que existe una cadena, pero no podemos asegurar que no existan
otras, ya que el argumento utilizado se puede volver a aplicar en el caso en
que
. Hay que hacer notar que lo único
que sabemos es que existe una cadena, pero no podemos asegurar que no existan
otras, ya que el argumento utilizado se puede volver a aplicar en el caso en
que ![]() tenga otro eigenvector
tenga otro eigenvector ![]() que sea independiente de los
mencionados anteriormente.
que sea independiente de los
mencionados anteriormente.
Todas estas consideraciones pueden ser aplicadas a ![]() misma.
misma.
Supongamos que ![]() tiene dos eigenvectores
tiene dos eigenvectores
![\begin{eqnarray*}[h,[f,g]] & = & [f,[h,g]]+[[h,f],g]\\
& = & [f,\mu g]+[\lambd...
...\
& = & \mu[f,g]+\lambda[f,g]\\
& = & (\mu + \lambda )[f,g]
\end{eqnarray*}](img914.gif)
Aquí la conclusión es que si tenemos dos eigenvectores con eigenvalores
![]() y
y ![]() , entonces el conmutador es otro eigenvector cuyo eigenvalor es la
suma de
, entonces el conmutador es otro eigenvector cuyo eigenvalor es la
suma de ![]() y
y ![]() y si
y si ![]() no es un eigenvalor, entonces
no es un eigenvalor, entonces ![]() .
.
Hasta aquí hemos considerado dos cosas
1a)
![]() , ya que
, ya que ![]() implica eigenvalores repetidos.
implica eigenvalores repetidos.
2a) ![]() es un operador normal.
es un operador normal.
Dado que los eigenvectores de un operador normal forman un conjunto
completo ortonormal, se nos presenta la posibilidad de utilizarlos para
representar a todos los demás.
Así, si todos los eigenvalores del operador ![]() son diferentes, todos sus
eigenvectores pueden ser diferenciados por medio de sus eigenvalores; es decir, el
eigenvector
son diferentes, todos sus
eigenvectores pueden ser diferenciados por medio de sus eigenvalores; es decir, el
eigenvector ![]() con eigenvalor
con eigenvalor ![]() será llamado
será llamado ![]() .
.
Pero si hay multiplicidad de eigenvalores, es decir, si tenemos al menos
dos eigenvectores linealmente independientes,
![]() con el mismo
eigenvalor
con el mismo
eigenvalor ![]() , entonces el símbolo
, entonces el símbolo ![]() no es suficiente
para caracterizar el vector. Un nuevo símbolo de distinción debe ser
introducido por ejemplo podríamos escribir
no es suficiente
para caracterizar el vector. Un nuevo símbolo de distinción debe ser
introducido por ejemplo podríamos escribir
![]() .
Basádos en el hecho de que dos operadores normales conmutativos tienen
un conjunto común de eigenvectores, podemos utilizar otra notación. Si
encontramos un segundo operador
.
Basádos en el hecho de que dos operadores normales conmutativos tienen
un conjunto común de eigenvectores, podemos utilizar otra notación. Si
encontramos un segundo operador ![]() que conmute con
que conmute con ![]() tal que
tal que

En caso dado en que este segundo operador no baste para identificar todos los eigenvectores, entonces se introduce otro, etc.. Así la idea de buscar una ``especie de conjunto maximal'' de operadores que conmuten entre sí.