Transformaciones infinitesimales

Vamos a ver que condición adicional, debe cumplir una transformación canónica para que sea una transformación que difiere en poco de la identidad es decir, las tranformaciones infinitesimales.

Recordemos que la condición para que una transformación sea canónica es que

$$M^T J \, M = J$$

Esta relación nos recuerda una anterior muy conocida, la cual es

$$O^T {\bf I} \, O = {\bf I}$$

Tomando en cuenta que la norma euclidiana de un vector está dada por

$$\Vert X\Vert^2 = \sum x_i^2 = X^TX$$

trataremos de averiguar un poco acerca de las transformaciones, $O$, las cuales preservan las norma, es decir,

$$\Vert OX\Vert = \Vert X\Vert$$

para lo cual desarrollamos $\Vert OX\Vert$

$$\Vert OX\Vert^2 = (OX)^T(OX) = (X^TO^T)\,(OT) = X^T (O^TO) \,X$$

y como queremos

$$\begin{eqnarray*} \Vert OX\Vert^2 & = & \Vert X\Vert^2 \end{eqnarray*}$$

entonces necesitamos tener

$$\begin{eqnarray*} X^T (O^TO) X & = & X^TX \end{eqnarray*}$$

Una condición suficiente para que la última identidad se cumpla es que

$$O^TO = {\bf I}$$

Probaremos que también es una condición necesaria, es decir si

$$X^T (O^TO) X = X^TX$$

entonces

$$O^TO = {\bf I}$$

Para hacer eso primero definimos

$$O^TO = P$$

Así tenemos

$$X^TPX = X^TX.$$

El vector $X$ está dado por

$$\left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right]$$

$X^T$ por

$$\left[\begin{array}{cccc} x_1&x_2&\ldots&x_n\end{array}\right]$$

y $P = (p_{ij})$

Por lo tanto el vector $PX$ estará dado por

$$\left[\begin{array}{c} \sum_{j=1}^n p_{1j}x_j \\ \\ \sum... ... \\ \vdots \\ \sum_{j=1}^n p_{nj}x_j \\ \end{array}\right]$$

multiplicando por $X^T$ a la izquierda

$$\begin{eqnarray*} X^T PX & = & \, [\, x_1,x_2, \ldots, x_n \, ] \left[ \begin{a... ...n p_{ij} x_ix_j \right) \\ & = & \sum_{i,j=1}^n p_{ij}x_i x_j \end{eqnarray*}$$

pero $X^TX = \sum_{i=1}^n x_i x_i$

por lo tanto;

$$\begin{eqnarray*} p_{ij}x_i x_j & = & \sum _{i=1}^n x_i x_j \end{eqnarray*}$$

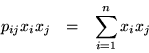
Pero esto se debe cumplir para cualquier vector que tiene en sus entradas solamente ceros excepto en la k-ésima que tiene un 1

Entonces tendríamos la relación:

$$\begin{array}{cccc} p_{kk}x_kx_k & = & x_k x_x & \; \mbox{ pero } \; x_k = 1 \end{array}$$

entonces

$$\begin{array}{cccc} p_{kk} & = & 1 & \end{array}$$

y esto es valido para toda $k$ tal que $1 \leq k \leq n$.

Ahora que sabemos que la matriz $P$ tiene solamente unos en la diagonal.

Utilizando el hecho de que

$$\begin{eqnarray*} P & = & O^TO \end{eqnarray*}$$

vemos que P es simétrica, ya que

$$\begin{eqnarray*} P^T & = & (O^TO)^T \\ & = & O^T (O^T)^T \\ & = & O^TO \end{eqnarray*}$$

de donde

$$P^T = P$$

y ahora haciendo uso de la relación 1 pero con el vector con un uno en la $i$-ésima y en la $k$-ésima entrada y ceros en las demás llegamos a que

$$\begin{eqnarray*} 2 + 2 P_{ik} & = & 2 \end{eqnarray*}$$

de aqui vemos que

$$\begin{array}{cccccc} P_{ik} & = & P_{ki} & = & 0 & \mbox{con } \quad i\neq k \end{array}$$

así tenemos que

$$P = {\bf I}$$

que es lo que queriamos probar.

Las matrices que cumplen con la relación

$$A^TA = {\bf I}$$

se llaman matrices ortogonales.

Se puede generalizar el concepto de norma definiéndolo de la manera siguiente:

$$\Vert X \Vert^2 = X^T G X$$

$$\Vert X \Vert^2 = \sum_{i,j=1}^n g_{ij} x_i x_j$$

Hay dos casos importantes

a) $G$ es una matriz simétrica

b) $G$ es una matriz antisimétrica

De aquí podemos ver que no necesariamente consideramos ortogonales a los vectores base.

Ahora nos preguntamos cuales son las transformaciones que guardan la norma.

Trabajando análogamente a como se hizo en el caso de la norma euclideana se llega a la conclusión de que las transformaciones requeridas cumplen con la condición:

$$M^T G M = G$$

Dedicaremos nuestra atención al caso, donde $G$ es la matriz antisimétrica

De aqui se puede observar que bajo condicines de simetría o de antisimetría, la condición de guardar una norma, es más o menos la condición que hemos visto que debe cumplir una transformacion para guardar la forma de un sistema hamiltoniano de ecuaciones.

Definimos una transformación Simpléctica M como aquella que cumple con:

$$M^T J M = J$$

Cuando hablamos de normas en el espacio vectorial real, los dos casos posibles para preservar una norma es que las transformaciones sean ortogonales o simplécticas.

Porque cuando $G$ es simétrica siempre podemos reducir esta a la matriz identidad mediante un cambio de base. Y cuando $G$ es antisimétrica la podemos reducir a la matriz J.

Los dos últimos resultados serán probados posteriormente.

Recordemos que el hecho de que una transformación sea o no canónica no depende del hamiltoniano. En cambío puede ocurrir que un sistema de coordenadas sea más adecuado, para un hamiltoniano, que otro.

Esto nos lleva a pensar que existen clases de equivalencia en el conjunto de sistemas de coordenadas.

Decimos que un sistema de coordenadas $S_1$ es equivalente al $S_1^{'}$ si existe una transformación simpléctica u ortogonal entre $S_1$ y $S_1^{'}$.

Puede suceder que por medio de alguna transformación lleguemos de $S_1$ y $S_1^{'}$ y que por medio de alguna transformación lleguemos de $S_2$ y $S_2^{'}$ y sin embargo de $S_1$ no podemos obtener $S_2^{'}$.

Esto no quiere decir que como sistema de coordenadas $S_1$ sea más valioso que $S_2$, sino que simplemente que para algunos problemas $S_1$ sea más adecuado y recíprocamente.

En resumen hay una clase de sistemas que pueden ser derivados de un sistema inicial, otra clase que puede ser derivada de otro sistema incial sin necesidad que los dos sistemas iniciales sean equivalentes.

Diremos que dos sistemas son equivalentes canónicamente si existe una transformación canónica tal que de uno podamos derivar el otro.

Recordemos que la condición para que una transformación sea canónica es que

$$M^T J M = J$$

y también que pueda preservar un producto interior definido por

$$(X,X) = X^T J X$$

La forma que tiene M es

$$\begin{eqnarray*} M & = & \left[ \begin{array}{cc} \frac{\partial P}{\partial... ...artial q} & \frac{\partial Q}{\partial q} \end{array} \right] \end{eqnarray*}$$

Ahora escribimos

$$M = {\bf I} + \varepsilon S$$

Justificamos esto por escribir

$$\begin{array}{cccc} P_j & = & p_j + \varepsilon \xi_j(p_i,q... ...\\ Q_j & = & q_j + \varepsilon \eta_j(p_i,q_i) & \end{array}$$

Así $P_j$ difiere de $p_j$ en muy poco y esto se deberá a la función $\xi_j$ que depende de $p_i$ y $q_i$.

Análogamente $Q_j$ difiere solamente por la variación de $\eta_j$ y entre más pequeño sea $\varepsilon$ menos diferencia vamos a ver entre $P_j$ y $p_j$ y entre $Q_j$ y $q_j$.

Esto es lo que entendemos por una transformación infinitesimal.

También podemos pedir que $\max \,\{ \vert \max \xi\vert, \vert\min \xi\vert, \vert\max \eta\vert, \vert\min \eta\vert\,\} < 1$.

Nuestro interés aumentará cuando $\varepsilon \rightarrow 0$.

Ahora M toma la forma siguiente:

$$\begin{eqnarray*} M & = & \left[ \begin{array}{cc} \delta_{ij} + \varepsilon ... ...on \frac{\partial \eta_{j}}{\partial q_i} \end{array} \right] \end{eqnarray*}$$

Cada término que hemos escrito en la matriz en realidad es una submatriz.

M puede ser escrita de la manera siguiente:

$$\begin{eqnarray*} M & = & \left[ \begin{array}{cc} {\bf I} & O \\ & \\ O & {\b... ... & \frac{\partial \eta_j}{\partial q_i} \end{array} \right] \end{eqnarray*}$$

Definiendo

$$\begin{eqnarray*} S & = & \left[ \begin{array}{cc} \frac{\partial \xi_j}{\par... ... & \frac{\partial \eta_j}{\partial q_i} \end{array} \right] \end{eqnarray*}$$

Por lo tanto

$$M = {\bf I} + \varepsilon S$$

Tenemos interés en el caso en que $\varepsilon \ll 1$ tal que $\varepsilon^2$ pueda despreciarse.

Ahora recordemos que

$$M^T J M = J$$

$$\begin{eqnarray*} \left[ \begin{array}{cc} \frac{\partial \xi_j}{\partial p_i... ... & \frac{\partial \eta_j}{\partial q_i} \end{array} \right] \end{eqnarray*}$$

El último resultado se debe a que si las matrices $A$, $B$, $C$, $D$ forman $S$, es decir.

$$\begin{eqnarray*} S & = & \left[ \begin{array}{cc} A & B \\ C & D \end{array} \right] \end{eqnarray*}$$

entonces

$$\begin{eqnarray*} S^T & = & \left[ \begin{array}{cc} A^T &C^T \\ B^T & D^T \end{array} \right] \end{eqnarray*}$$

y

$$\begin{eqnarray*} S^TJ+JS & = & \left[ \begin{array}{cc} \frac{\partial \xi... ...frac{\partial \eta_j}{\partial p_i} \end{array} \right] =\, 0 \end{eqnarray*}$$

$$\begin{eqnarray*} ({\bf I}+\varepsilon S)^T J ({\bf I}+\varepsilon S) & = & J \... ...= & J \\ (J+\varepsilon S^TJ) ({\bf I}+\varepsilon S) & = & J \end{eqnarray*}$$

como

$$\varepsilon^2 \ll 1$$

$$J + \varepsilon JS + \varepsilon S^TJ=J$$

Así

$$J+\varepsilon (S^TJ+JS) = J$$

entonces

$$S^TJ+JS = O$$

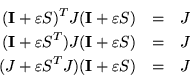
Y ésta es la condición que debe cumplir la matriz S con el objeto de que la transformación infinitesimal sea canónica, mejor dicho aproximadamente canónica y entre menor sea $\varepsilon$ tendremos una mayor aproximación a una transformación canónica.

Escribiendo esto en términos de elementos de matriz

$$S^TJ+JS = O$$

tenemos

$$\begin{eqnarray*} \frac{\partial \xi_i}{\partial q_j} &=& \;\; \frac{\partial \x... ...a_i}{\partial p_j}&=& \;\; \frac{\partial \eta_j}{\partial p_i} \end{eqnarray*}$$

Escribamos las últimas ecuaciones con otra notación.

$$\frac{\partial X_i}{\partial \chi_j}=\frac{\partial X_j}{\partial \chi_i}$$

Pero estas son las condiciones necesarias y suficientes, cuando trabajamos en un dominio simplemente conexo. Para que exista una función cuya diferencial es exacta. Denotando esta función por V tenemos:

$$X_k=\frac{\partial V}{\partial \chi_k}$$

Regresando a nuestra notación anterior, lo que sabemos es que existe una función $S(p,q)$ tal que

$$\begin{eqnarray*} \xi_j & = & \;\; \frac{\partial S}{\partial q_j} \\ \eta_j& = & -\frac{\partial S}{\partial p_j} \end{eqnarray*}$$

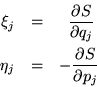
Así la condición necesaria y suficiente en el jacobiano para una transformación infinitesimal sea canónica, es que las derivaciones en las coordenadas sean las derivadas de una función S, como la mencionada.

Es necesario y suficiente si tomamos en cuenta la continuidad y la no singularidad del jacobiano.

El jacobiano no es cero, para un $\varepsilon$ suficientemente pequeño ya que los unos en la diagonal dominarán.

La existencia de una función $S$, a la cual llamaremos la generadora de la transformación infinitesimal, nos permite expresar el cambio de cualquier función $f(P,Q)$.

Ya que

$$f(P,Q)=f(p+\varepsilon\xi,q+\varepsilon\eta)$$

y si $f$ admite un desarrollo en serie de Taylor

$$f(P,Q) = f(p,q) + \varepsilon \sum \left( \frac{\partial f}... ...tial^2 f}{\partial q^2} \eta^2 + \varepsilon^3 \ldots \right)$$

Introduzcamos ahora las relaciones que tenemos para la función generadora.

Recordando la definición del paréntesis de Poisson, podemos escribir el término en $\varepsilon$ como

$$\varepsilon\sum \left(\frac{\partial f}{\partial p_i}\frac{\p... ..._i}\frac{\partial S}{\partial p_i}\right) = \varepsilon\{f,S\}$$

y hasta términos de orden $\varepsilon$ podemos ver el cambio de cualquier función que depende en coordenadas canónicas cuando hacemos un cambio de éstas.

Si $f(p,q)$ se vé en otras coordenadas $P$, $Q$

$$\begin{array}{ccccc} f(p,q) & \rightarrow & f(P,Q) & = & f(p,q) + \varepsilon \{f,S\} \end{array}$$

cuando

$$\begin{eqnarray*} p & \rightarrow & p + \varepsilon \frac{\partial S}{\partial ... ...q & \rightarrow & q + \varepsilon \frac{\partial S}{\partial p} \end{eqnarray*}$$

Entonces podemos apreciar que cuando $p$, $q$ varían un poco, también va a resultar un pequeño cambio en la función que dependa en $p$ y $q$, y este cambio puede expresarse, hasta términos en orden $\varepsilon$, por los paréntesis de Poisson.

Esta es la segunda aplicación que encontramos para los paréntesis de Poisson.

El primer empleo fué el criterio para ver si una transformación finita y macroscópica es canónica. La tabla de paréntesis de Poisson entre variables y coordenadas tiene que representar la matriz antisimétrica $J$.

Veamos ahora un caso particular, pero que es muy interesante e importante

$$\begin{eqnarray*} \frac{df}{dt} &=& \; \; \frac{\partial f}{\partial p}\dot{p} ... ...rtial t}\\ & = & \; \; \{f,h\} +\frac{\partial f}{\partial t} \end{eqnarray*}$$

y cuando f no depende explícitamente en el tiempo $\frac{\partial f}{\partial t} = 0$ y por lo tanto

$$\frac{df}{dt} = \{f,H\}$$

y entonces la derivada de la función está expresada por un paréntesis de Poisson.

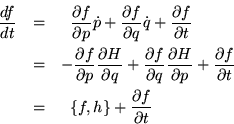
Hemos visto como podemos caracterizar una transformación infinitesimal para que sea canónica, y como esto implica la existencia de una función tal que los cambio entre las coordenadas antiguas y las nuevas pueden ser expresados como derivadas de esa función generadora.

El proceso contrario es completamente admisible, es decir, uno puede tomar una función arbitraria y con ésta generar una transformación infinitesimal canónica.