Si queremos ahora, que el nuevo sistema de coordenadas
![]() se preserve la ``forma" de las
ecuaciones, es decir, que
se preserve la ``forma" de las
ecuaciones, es decir, que
Aquellas transformaciones tales que cumplan con (1.10) seran llamadas canónicas.
Cabe hacer notar que cuando J es simplemente una matriz antisimétrica
no singular entonces las transformaciones que cumplen con
Entonces las transformaciones canónicas son un caso especial de las simplécticas.
Veamos ahora las condiciones que deben cumplir los elementos de la
matriz M para que tengamos una transformación canónica; estas serán
obtenidas de la relación de definición.
![]() que es la matriz jacobiana de la transformación la escribiremos como
que es la matriz jacobiana de la transformación la escribiremos como
Recordando que si tenemos una matriz subdividida en submatrices
digamos que
![\begin{displaymath}\begin{array}{ccc}
JM & = & \left[ \begin{array}{cc}
-\fr...
...ac{\partial Q^T}{\partial p}
\end{array} \right]
\end{array}\end{displaymath}](img109.gif)
![\begin{displaymath}\begin{array}{ccl}
M^TJM & = &
\left[ \begin{array}{cc}
...
...rac{\partial Q^T}{\partial p}
\end{array} \right]
\end{array}\end{displaymath}](img111.gif)
Pero ![]() nos dice que
nos dice que
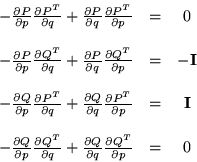
Estas condiciones las podemos escribir para cada uno de los elementos
que forman las matrices y estas serán:
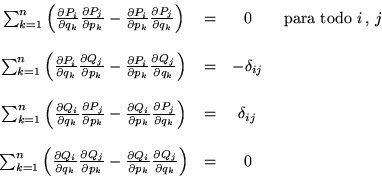
Así, estas ![]() ecuaciones expresan en términos de elementos
matriciales, las condiciones necesarias y suficientes para que una
transformación sea una transformación canónica.
ecuaciones expresan en términos de elementos
matriciales, las condiciones necesarias y suficientes para que una
transformación sea una transformación canónica.
Dentro de la mecánica clásica este tipo de ecuaciones se presentan muy
frecuentemente y por eso vale la pena darle un nombre, entonces definimos el
paréntesis de Poisson de ![]() y
y ![]() con respecto a las variables
con respecto a las variables
![]() como
como
Con esta notación nuestras condiciones para que una transformación sea
canónica, serán:
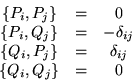
Veamos ahora dos ejemplos:
Ejemplo 1.
tomemos
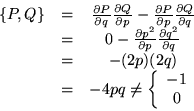
Por tanto podemos afirmar que no tenemos una transformación canónica.
Ejemplo 2.
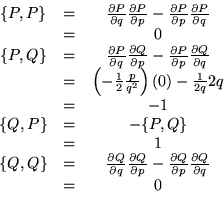
Así vemos que ésta sí es una transformación canónica.
Regresemos a nuestra relación
tomando inversos tenemos
pero
así
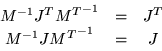
Con la notación usada en (1.11) y utilizando la propiedad de los
jacobianos enunciada en (1.8a) tenemos que
![\begin{displaymath}\begin{array}{ccc}
{M^T}^{-1} & = &
\left[ \begin{array}{...
...\frac{\partial q}{\partial Q}
\end{array} \right]
\end{array}\end{displaymath}](img127.gif)
![\begin{displaymath}\begin{array}{ccc}
M^{-1} & = &
\left[ \begin{array}{cc} ...
...\frac{\partial q}{\partial Q}
\end{array} \right]
\end{array}\end{displaymath}](img128.gif)
![\begin{displaymath}\begin{array}{ccc}
M^{-1} & = &
\left[ \begin{array}{cc} ...
...rac{\partial q^T}{\partial Q}
\end{array} \right]
\end{array}\end{displaymath}](img129.gif)
Tomemos el producto ![]()
![\begin{displaymath}\begin{array}{ccl}
J{M^T}^{-1} & = &
\left[ \begin{array}...
...\frac{\partial p}{\partial Q}
\end{array} \right]
\end{array}\end{displaymath}](img131.gif)
![\begin{displaymath}\begin{array}{ccl}
M^{-1}J{M^T}^{-1} & = &
\left[ \begin{...
...\frac{\partial p}{\partial Q}
\end{array} \right]
\end{array}\end{displaymath}](img132.gif)
Así
![]() implica:
implica:
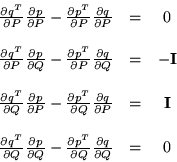
Escribiremos ahora estas condiciones, por medio de los elementos
matriarcales, recordando primero como estan dadas las matrices que
intervienen en las anteriores igualdades.
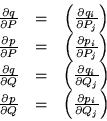
Las condiciones son entonces:
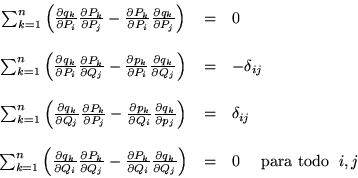
Por los mismos motivos que se introdujeron los paréntesis de Poisson
se introducen los de Lagrange. Por tanto definiremos el paréntesis de
Lagrange de ![]() y
y ![]() con respecto a las variables
con respecto a las variables
![]() como
como
Con esta notación nuestras cuatro condiciones quedan como
![\begin{displaymath}\begin{array}{ccc}
{[}P_i,P_j{]} & = & 0 \\
{[}P_i,Q_j{]}...
..._j{]} & = & \delta_{ij} \\
{[}Q_i,Q_j{]} & = & 0
\end{array}\end{displaymath}](img141.gif)
Consideremos la transformación identidad, la cual cumple con

![\begin{displaymath}\begin{array}{ccc}
{[}p_i,p_j{]} & = & 0 \\
{[}p_i,q_j{]}...
..._j{]} & = & \delta_{ij} \\
{[}q_i,q_j{]} & = & 0
\end{array}\end{displaymath}](img145.gif)