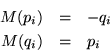Definimos el espacio vectorial ![]() como todas las combinaciones
lineales generadas por el conjunto de funciones
como todas las combinaciones
lineales generadas por el conjunto de funciones
![]() que cuando se evaluan nos dan la cantidad
de movimiento o la coordenada. Notamos que
que cuando se evaluan nos dan la cantidad
de movimiento o la coordenada. Notamos que
Es conveniente hablar de una sola variable para denotar los elementos de la base, así definimos:
Definimos una transformación ![]() de la siguiente manera:
de la siguiente manera:
El que ![]() es un operador lineal se deriva del hecho de que los
paréntesis de Poisson son lineales, es decir,
es un operador lineal se deriva del hecho de que los
paréntesis de Poisson son lineales, es decir,
Pero como ya sabemos, en un espacio vectorial para cada transformación
existe una representación matricial de ella, así para toda ![]() nosotros
podemos tener una representación matricial de
nosotros
podemos tener una representación matricial de ![]() .
.
Veamos algunos ejemplos, usando las reglas canónicas:
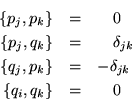
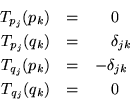
Para clarificar ideas que serán desarrolladas posteriormente formamos
la siguiente tabla
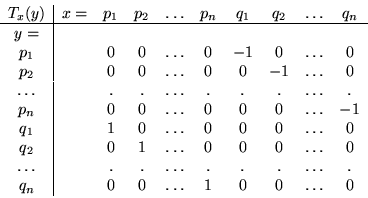
Vemos que esta tabla es la matriz ![]() , y que
, y que
![]() es un
conjunto generador del espacio dual, ya que sólo difiere de la base dual,
en que unas funciones tienen un factor de
es un
conjunto generador del espacio dual, ya que sólo difiere de la base dual,
en que unas funciones tienen un factor de ![]() .
.
Denotamos el espacio dual por
![]() .
.
Ahora construyamos la base dual. Denotémosla por ![]()
Recordando que
Si vemos nuestra tabla notamos que nuestra función ![]() cumple
con esta propiedad y además que para
cumple
con esta propiedad y además que para ![]()
Ahora solo nos resta encontrar las
![]()
Para ![]() debemos tener
debemos tener
Así
En resumen la base dual es:
Ahora definimos el conjugado canónico del vector ![]() como aquel
vector
como aquel
vector ![]() tal que
tal que
Así vemos que el conjugado canónico de ![]() es
es ![]() , y el de
, y el de ![]() es
es ![]() .
.
Debido a ![]() es también una base del espacio
es también una base del espacio ![]() vemos que en realidad el tomar el conjugado canónico es una función entre
dos bases del mismo espacio. Denotemos esta función por
vemos que en realidad el tomar el conjugado canónico es una función entre
dos bases del mismo espacio. Denotemos esta función por ![]() , así
, así