Sobre el espacio dual ${\Phi _n^{(1)}}^+$

Recordando que el paréntesis de Poisson es una función bilineal, usando la linealidad en el primer argumento, tenemos que $M$ es una función lineal, por lo tanto existe una matriz la cual nos va a representar a la transformación $M$. Y esta matriz es $J$.

Es importante notar que nuestra funcional lineal $T_f$, definida como

$$T_f(g) = \{f,g\}$$

cuando $f$ y $g$ pertenecen entonces tenemos que

$$T_f(g)$$

pertenece a $\Phi_n^{(0)}$ = ${\cal C}$ o ${\cal R}$.

Gracias a la linealidad en el primer argumento en el paréntesis de Poisson:

$$\begin{eqnarray*} T_{\alpha f + \beta g}(h) & = & \{\alpha f + \beta g,h\} \\ ... ...\{f,h\} + \beta \{g,h\} \\ & = & \alpha T_f(h) + \beta T_g(h) \end{eqnarray*}$$

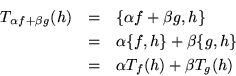
lo cual quiere decir que podemos formar combinaciones lineales de las funciones en el espacio dual, por formar la misma combinación lineal con los índices.

Así tenemos que

$${\Phi_n^{(1)}} \sim {\Phi_n^{(1)}}^{+}$$

Hagamos más explícito el hecho de este isomorfismo.

Definamos $\Psi: \Phi_n^{(1)}\rightarrow {\Phi_n^{(1)}}^+$ de la siguiente manera:

$$\Psi(f) = T_f$$

donde

$$T_f(g) = \{f,g\}$$

veamos ahora que $\qquad \Psi(\alpha f + \beta g) = \alpha \Psi(f) + \beta \Psi(g)$

$$\Psi(\alpha f + \beta g) = T_{\alpha f + \beta g} = \{\al... ... = \alpha T_f + \beta T_g = \alpha \Psi(f) + \beta \Psi(g)$$

El hecho de tener una base en un espacio, nos permite definir un producto interno lo cual denotaremos por (f, g). Si $f = \sum c_i x_i$     ,      $g = \sum d_i x_i$,

$$(f,g) \stackrel{\rm def}{=} \sum c_i d_i$$

donde $\{ x_i \}$ es una base.

Este producto nos definirá una norma pitagoreana.

En el caso en que nuestro campo de escalares sean los complejos trabajaremos con una norma hermitiana dada por un producto interno definido de la siguiente manera:

$$(f,g) \stackrel{\rm def}{=} \sum c^*_i \,d_i$$

donde $c^*_i$ es el conjugado complejo de $c_i$.

Nosotros trabajaremos esta última definición.

En este punto es bueno recordar algunas propiedades de los espacios vectoriales cuando tienen definidos sobre ellos dos estructuras como son nuestra función lineal definida por;

$$\phi(x,y) = \sum c_i d_i$$

y nuestra funcional sesquilineal dada por

$$(x,y) = \sum c^*_i d_i$$

Sabemos por el teorema de Riesz que puede expresarse como;

$$(x,y) = \phi(Ax,y)$$

donde $A$ es una transformación lineal sobre nuestro espacio.

Debido a esta igualdad si nosotros conocemos las propiedades que tiene el producto interior Pitagoreano con sólo tener la transformación $A$, es decir, una matriz, conoceremos las propiedades del producto Hermitiano.

En realidad lo importante de esto es que se cumple para cualesquiera dos productos internos.

Ahora regresemos al espacio $\Phi _n^{(1)}$ y a su espacio dual.

Por ser $\Phi _n^{(1)}$ un espacio de dimensión $2n$, sabemos que es isomorfo al espacio vectorial de 2n-adas $x_1, x_2, \ldots, x_{2n}$ que son renglones. Su espacio dual ${\Phi _n^{(1)}}^+$ es isomorfo también a ese espacio, pero nosotros preferimos establecer la correspondencia con el espacio vectorial de 2n-adas,

$$\mbox{ }\left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right]$$

que son columnas.

Es claro que hace una correspondencia entre estos dos espacios, de vectores columna y vectores renglón, a la correspondencia que mostramos se le llama Transposición

$$\left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{arra... ...n{array}{cccc} x_1, & x_2, & \ldots, & x_n \end{array} \right]$$

Así con cada vector de $\Phi _n^{(1)}$ tendremos asociado un vector renglón. Y con cada funcional lineal que opere sobre $\Phi _n^{(1)}$ tendremos asociada un vector columna.

Nosotros asociaremos por el momento

$$\begin{eqnarray*} p_1 & \rightarrow & \left[ \begin{array}{c} 1 \\ 0 \\ \vdots... ...\ 0 \\ \vdots \\ 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{array} \right] \end{eqnarray*}$$

Bajo esta asociación, el producto interno de dos vectores cualesquiera de $\Phi _n^{(1)}$ nos dará el mismo resultado que el producto interno de los vectores columna asociados. Basándonos en esto tenemos que si $x$, $y$ pertenecen a $\Phi _n^{(1)}$ entonces

$$(x,y) = (c,c^\prime)$$

donde por las $c'$s denotaremos los correspondientes vectores columna a $x$ y $y$.

Como sabemos que una funcional lineal, es decir, un elemento de un espacio dual puede ser expresada como un producto interno entre elementos del espacio dual, tenemos:

$$\varphi(x) = (c,c^\prime)$$

donde $\varphi$ es una función que le corresponde una vector columna $c$. O lo que es lo mismo habrá otra funcional lineal sobre el espacio de los vectores columna tal que

$$\xi(c) = \varphi(x) = (c,c^\prime) = (x,y)$$

Ahora en base a que $\varphi$ puede representarse como una columna, nos preguntamos si habrá una operación entre renglones y columnas tal que produzca el mismo efecto de evaluar $\varphi(x)$.

La contestación es sí, y la operación es la operación de multiplicar matrices, así sí:

$$\varphi \rightarrow \left(\alpha_1 , \alpha_2 , \ldots, \alpha_n \right)$$

y

$$\chi \rightarrow \left[\begin{array}{c}\chi_1\\ \chi_2\\ \vdots\\ \chi_n\end{array}\right]$$

entonces

$$\varphi(\chi) = \left(\alpha_1,\alpha_2,\ldots,\alpha_n \rig... ...{array}{c}\chi_1\\ \chi_2\\ \vdots\\ \chi_n\end{array}\right]$$

pero sabemos que

$$\varphi(\chi) = (x,y)$$

entonces si $y$ está representado por

$$\left[\begin{array}{c} y_1 \\ y_2\\ \vdots \\ y_n \end{array}\right]$$

tenemos que

$$(x,y) = \sum \chi^*_i y_i = \sum \alpha_ix_i$$

cuando $x = y$

$$\sum \alpha_i y_i = \sum y^*_i y_i$$

Esto sucede para todo vector, en particular sucederá para un vector que sea representado por

$$\left[\begin{array}{c} 0 \\ \vdots\\ a_j+ib_j \\ 0 \\ \vdots \\ 0 \end{array}\right]$$

Entonces tendremos que

$$\alpha_j = \overline{y}_j$$

Así

$$\begin{eqnarray*}\varphi & & (\overline{y}_1,\overline{y}_2, \ldots,\overline{y}_n) \end{eqnarray*}$$

y como

$$y \rightarrow \left[\begin{array}{c} y_1\\ y_2\\ \vdots \\ y_n \end{array}\right]$$

Su asociado en el dual será el conjugado transpuesto.

Así tenemos una correspondencia entre el dual y el espacio, y esta es, que a cada vector renglón le asociamos un vector del dual el cual será, el transpuesto conjugado.