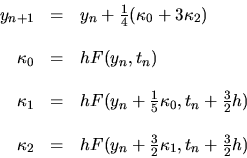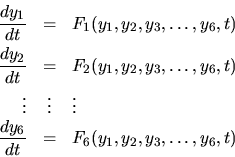Next: Descripción del programa
Previous: Generalidades sobre el monopolo
Contents
En este capítulo vamos a discutir el método usado en
nuestro trabajo para resolver las ecuaciones de movimiento. Hay
muchos métodos numéricos para integrar ecuaciones
diferenciales y su aplicabilidad depende del tipo de ecuación
que se esté tratando. Uno de los métodos más simples y que
es muy confiable, es el de Runge-Kutta en varias versiones como
explicaremos a continuación.
2.1
Supóngase una ecuación (trataremos por el momento con una sola
variable) de la forma
donde  es del tipo
es del tipo
La gráfica de la función se representará como en la
Figura 2.1. Las derivadas de dicha función se conocen en
todo punto, ya que vienen especificadas por la ecuación
diferencial. Si  es el incremento de tiempo, entonces, a
primera aproximación, se tendrá como valor de la función
después de un tiempo
es el incremento de tiempo, entonces, a
primera aproximación, se tendrá como valor de la función
después de un tiempo  , la cantidad
, la cantidad
esto puede representarse en la Figura 2.1
Figure 2.1:
derivada
 |
En el caso no lineal que es el que nos interesa se escribe
aunque eso no es precisamente correcto debido a la no
linealidad. Como se ve, este método consiste en tomar una nueva
derivada después de cierto tiempo, y así sucesivamente,
porque la tangente a la curva está cambiando constantemente su
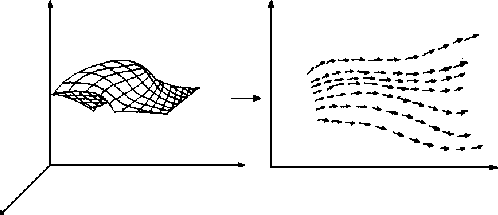
dirección. Puede entenderse a la función  como una
superficie en tres dimensiones de la cual nos trasladamos a un
campo de tangentes como indica el siguiente dibujo.
como una
superficie en tres dimensiones de la cual nos trasladamos a un
campo de tangentes como indica el siguiente dibujo.
Figure 2.2:
flechas
 |
En cada punto habrá una flecha indicando en que dirección hay
que moverse. Con este procedimiento no se sigue exactamente a la
curva pero se puede confiar en que escogiendo  suficientemente
pequeño habrá un error
suficientemente
pequeño habrá un error 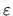 , de tal manera que el
resultado final diferirá del valor real por una cantidad del
orden de
, de tal manera que el
resultado final diferirá del valor real por una cantidad del
orden de 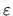 .
.
El método que acabamos de exponer se conoce como ``Método de
Euler'' y no es nuestro propósito discutirlo aquí con todo su detalle.
La técnica puede mejorarse si en vez de una recta se toma por ejemplo
una parábola tangente a cada punto de la curva.
2.2
Considere ahora la ecuación 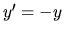 , si se toma
, si se toma  en
en  , al desarrollar la función en serie de potencias alrededor de
, al desarrollar la función en serie de potencias alrededor de
 se tiene:
se tiene:
eso debido a que
No hay ningún argumento que impida desarrollar ``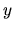 '' en serie de
potencias pero si se toma la función en toda su generalidad se tendrá
'' en serie de
potencias pero si se toma la función en toda su generalidad se tendrá
Los subíndices significan derivación parcial con respecto a la
variable indicada; entonces, para
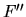 se tendra
se tendra
Se cambió el órden de la derivación. Sustituyendo  resulta lo siguiente:
resulta lo siguiente:
Resumiendo, se tiene para las tres primeras derivadas:
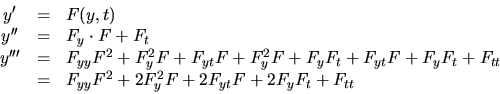 |
(II-2-1) |
Por el mismo procedimiento pueden ser encontradas las derivadas de
orden superior. Simbólicamente se resuelve la ecuación diferencial
tomando todas las derivadas formando así una serie de Taylor lo que no
es práctico porque hay que efectuar una cantidad de cálculos muy grande
y tediosa, y eso para cada ecuación diferencial que se presente.
2.3
Nuestro deseo es conocer una
técnica más general que permita resolver cualquier ecuación
diferencial, sin necesidad de conocer su forma precisa, para
obtener las derivadas; el método que emplearemos permite
calcularlas de otra manera. La base de este concepto es que
existen muchas funciones lineales, por ejemplo, los polinomios
forman un espacio vectorial (espacio dual) y por lo tanto puede
formarse una base en ese espacio de manera que toda función
analítica puede expresarse como una combinación lineal de
elementos de dicha base. Los polinomios tiene propiedades muy
interesantes, por ejemplo, en un polinomio de segundo grado basta
conocer tres valores diferentes de la función para conocer su
comportamiento en cualquier otro punto y de esa manera puede
encontrarse su derivada como combinación de los tres valores
conocidos.
Es bien sabido que tres puntos determinan una parábola, de la
manera siguiente:
Esta expresión puede también escribirse como un determinante:
Esta situación se representa en la Figura 2.3:
Figure 2.3:
parábola
 |
Al hacer operaciones se obtiene un polinomio de segundo grado,
así, puede calcularse fácilmente 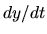 porque es una suma
de productos y diferencias. Con el objeto de evitar una gran
cantidad de pasos algebraicos se procede en una forma equivalente
pero más sencilla como veremos en seguida:
porque es una suma
de productos y diferencias. Con el objeto de evitar una gran
cantidad de pasos algebraicos se procede en una forma equivalente
pero más sencilla como veremos en seguida:
Figure 2.4:
curva
 |
Se toma un punto, definido por
 ,
donde la función expresa la derivada de cualquier curva que pase
por ese punto; posiblemente no la curva que nos interesa sino
alguna que pase precisamente por ahí con esa derivada,
Figura 2.4.
Esperamos obtener las derivadas de F en diversos de tales puntos.
Dibujemos esta función en tres dimensiones, representando un
cambio como el que acabamos de mencionar, Figura 2.5.
,
donde la función expresa la derivada de cualquier curva que pase
por ese punto; posiblemente no la curva que nos interesa sino
alguna que pase precisamente por ahí con esa derivada,
Figura 2.4.
Esperamos obtener las derivadas de F en diversos de tales puntos.
Dibujemos esta función en tres dimensiones, representando un
cambio como el que acabamos de mencionar, Figura 2.5.
Figure 2.5:
superficie
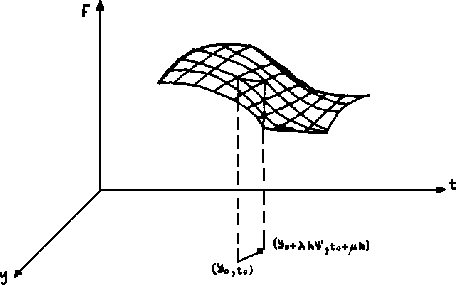 |
Desarróllese la función en serie de potencias alrededor del
punto escogido de la manera anterior y utilizando los parámetros
indicados, eso es
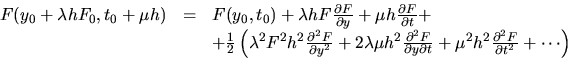 |
(II-3-1) |
La pendiente en este punto, entonces, queda expresada en términos de la
pendiente en el punto original, teniendo en cuenta que F como función
de dos variables puede desarrollarse en serie de potencias, como acaba
de hacerse.
Esta ecuación contiene las derivadas deseadas; la idea consiste en
invertirla. Esto se hace por un procedimiento más sencillo, por
ejemplo, escribiendo 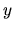 como:
como:
Se considerará la hipótesis de suponer para 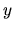 un desarrollo de la
forma:
un desarrollo de la
forma:
donde 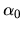 y
y 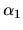 , son coeficientes, mientras que
, son coeficientes, mientras que
 y
y 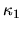 se definen como
se definen como
se tienen dos valores de  , uno en cada punto; puede
identificarse a
, uno en cada punto; puede
identificarse a  como el término
como el término  ,
, 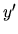 que se
introdujo en (II-1-2). Al expresar
que se
introdujo en (II-1-2). Al expresar 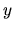 en términos de esas dos
cantidades se evita el problema de trabajar con las derivadas; el
procedimiento es tan legítimo como lo es el obtener la
función, la derivada y la segunda derivada usando tres puntos de
la curva. Que dicho procedimiento sea o no correcto depende de
qué tanto coinciden las series (II-3-2) y (II-3-3). Entonces, en
lugar de tener que invertir el desarrollo (II-3-1) se supone que
en términos de esas dos
cantidades se evita el problema de trabajar con las derivadas; el
procedimiento es tan legítimo como lo es el obtener la
función, la derivada y la segunda derivada usando tres puntos de
la curva. Que dicho procedimiento sea o no correcto depende de
qué tanto coinciden las series (II-3-2) y (II-3-3). Entonces, en
lugar de tener que invertir el desarrollo (II-3-1) se supone que
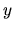 puede expresarse en la forma que hemos indicado y se verá
que error resulta al hacer esa consideracion. El error es,
naturalmente, la diferencia entre las expresiones (II-3-2) y
(II-3-3).
Al substituir
puede expresarse en la forma que hemos indicado y se verá
que error resulta al hacer esa consideracion. El error es,
naturalmente, la diferencia entre las expresiones (II-3-2) y
(II-3-3).
Al substituir  y
y 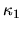 , en la segunda de estas series se
tiene
, en la segunda de estas series se
tiene
haciendo también una substitución en (II-3-2) y usando
(II-3-1) resulta
Por comparación de (II-3-4) y (II-3-5) se observa que son muy
próximas una de otra si los coeficientes de las mismas potencias
de  son aproximadamente iguales, o sea, que
son aproximadamente iguales, o sea, que
Si la aproximación no representa a 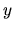 , por lo menos, la
diferencia entre aquella y el caso real tiende a cero a tercer
orden en
, por lo menos, la
diferencia entre aquella y el caso real tiende a cero a tercer
orden en  . Como deseamos que el método tenga validez general,
debemos pedir que se cumplan las relaciones
. Como deseamos que el método tenga validez general,
debemos pedir que se cumplan las relaciones
Si esto se cumple, podemos confiar en nuestro método. Como
tenemos cuatro incógnitas y sólo tres ecuaciones, el sistema
esta indeterminado, pero si se toma 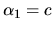 por ejemplo,
entonces todas las soluciones quedan en términos del parámetro
por ejemplo,
entonces todas las soluciones quedan en términos del parámetro
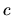 y se tendrá por consiguiente
y se tendrá por consiguiente
un valor muy favorecido para 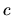 es
es 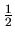 porque de esa
manera se tiene
porque de esa
manera se tiene
La selección de 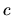 de ninguna manera aumenta el orden de
aproximación (igualar términos en
de ninguna manera aumenta el orden de
aproximación (igualar términos en 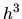 ) sino que simplifica
el cómputo si se toma un valor adecuado.
La técnica que acabamos de exponer es conocida como ``Método
de Runge-Kutta'' y puede extenderse para incluir aproximaciones de
orden mayor en las potencias de
) sino que simplifica
el cómputo si se toma un valor adecuado.
La técnica que acabamos de exponer es conocida como ``Método
de Runge-Kutta'' y puede extenderse para incluir aproximaciones de
orden mayor en las potencias de  .
Escribiendo la fórmula de Runge-Kutta para cualquier punto se tiene
.
Escribiendo la fórmula de Runge-Kutta para cualquier punto se tiene
donde
Al usar el valor convenido anteriormente para 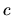 , resulta
, resulta
 |
(II-3-6) |
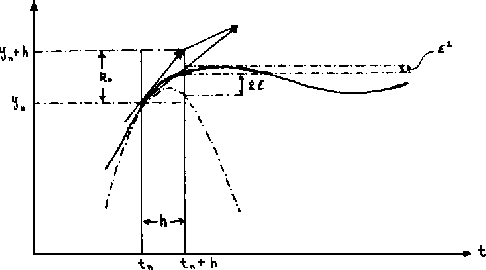
Gráficamente, el proceso puede extenderse de la manera
siguiente: Primero hay que formar  que es el incremento
vertical de la figura; con
que es el incremento
vertical de la figura; con 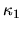 se realiza el segundo paso
de Euler en el punto
se realiza el segundo paso
de Euler en el punto
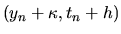 . La fórmula (II-3-6)
dice que hay que sumar los dos incrementos y el error obtenido es
del orden de
. La fórmula (II-3-6)
dice que hay que sumar los dos incrementos y el error obtenido es
del orden de 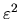 cuando hay un error de
cuando hay un error de 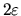 al ajustar nuestro elemento de arco con la parábola.
al ajustar nuestro elemento de arco con la parábola.
Figure 2.6:
 |
Cuando se hacen los cálculos a tercer orden el error irá como
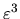 y el punto resultante se toma como el peso de tres
incrementos.
Existen varios métodos de Runge-Kutta y su elaboración es
más o menos la misma. Hay otros métodos y todos ellos suponen
que son conocidas las derivadas. La ventaja de los métodos de
Runge-Kutta está en que no hay que calcular derivadas, además,
es posible modificar el intervalo (se aumenta o se reduce el
incremento ) de acuerdo con la variación de la tangente. El
inconveniente que representan estos métodos es el de que hay que
realizar un gran número de cálculos para obtener
y el punto resultante se toma como el peso de tres
incrementos.
Existen varios métodos de Runge-Kutta y su elaboración es
más o menos la misma. Hay otros métodos y todos ellos suponen
que son conocidas las derivadas. La ventaja de los métodos de
Runge-Kutta está en que no hay que calcular derivadas, además,
es posible modificar el intervalo (se aumenta o se reduce el
incremento ) de acuerdo con la variación de la tangente. El
inconveniente que representan estos métodos es el de que hay que
realizar un gran número de cálculos para obtener  y cada
paso está basado en los anteriores.
En general, supóngase que
y cada
paso está basado en los anteriores.
En general, supóngase que 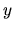 es un punto sobre la curva y que
puede escribirse en términos de uno de sus valores anteriores
más multiplos de
es un punto sobre la curva y que
puede escribirse en términos de uno de sus valores anteriores
más multiplos de  en diferentes puntos. Se expresa
en diferentes puntos. Se expresa 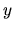 en
serie de potencias y se comparan los dos desarrollos. En otras
palabras, suponemos que:
en
serie de potencias y se comparan los dos desarrollos. En otras
palabras, suponemos que:
Aquí, la aproximación (el órden) depende del número de
puntos que se consideren, uno para la primera aproximación, dos para
la segunda, etc. Además, se supone, como hemos mencionado, que
El plan es el mismo que en caso anterior; hay que expresar 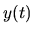 en términos de
en términos de  y elaborar
y elaborar  en varios puntos para
obtener una serie; los valores de
en varios puntos para
obtener una serie; los valores de  se obtienen con ayuda de la
ecuación diferencial. Hecho todo lo anterior, la tarea consiste
en seleccionar los coeficientes de tal manera que haya una
correspondencia, válida hasta la potencia deseada.
se obtienen con ayuda de la
ecuación diferencial. Hecho todo lo anterior, la tarea consiste
en seleccionar los coeficientes de tal manera que haya una
correspondencia, válida hasta la potencia deseada.
2.4
Presentamos ahora varios resultados sin entrar en más
detalles, ya que el procedimiento es el mismo que se discutió en
páginas anteriores. En (II-3-7) se escribe la fórmula hasta
tener órden, lo que significa que el error es a cuarto órden
en  . En ese caso se tiene
. En ese caso se tiene
 |
(II-4-1) |
Esta fórmula se atribuye a Kutta. Hay otra que se atribuye a Heun y
es la siguiente:
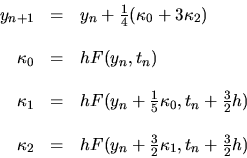 |
(II-4-2) |
Nótese que en el incremento de la función no aparece 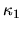 .
Este sólo se usa como un paso intermedio.
Con un método de Runge-Kutta a cuarto orden se obtiene
.
Este sólo se usa como un paso intermedio.
Con un método de Runge-Kutta a cuarto orden se obtiene
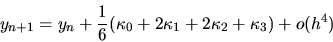 |
(II-4-3) |
 |
(II-4-4) |
Este es el método que usaremos para integrar nuestras ecuaciones
diferenciales. Cuando  no depende del tiempo se reduce al
método de Simpson. Puede hacerse un diagrama semejante a los que
se han hecho anteriormente pero resulta muy complicado, de modo
que con los que ya se tienen dan una idea acerca del tipo de
gráfica que se obtendría aquí.
El único problema que nos queda es el de introducir las
extrapolaciones convenientes. En nuestro caso resultan ecuaciones
de movimiento vectoriales, lo que significa que existe un vector
que depende del tiempo según la ecuación.
no depende del tiempo se reduce al
método de Simpson. Puede hacerse un diagrama semejante a los que
se han hecho anteriormente pero resulta muy complicado, de modo
que con los que ya se tienen dan una idea acerca del tipo de
gráfica que se obtendría aquí.
El único problema que nos queda es el de introducir las
extrapolaciones convenientes. En nuestro caso resultan ecuaciones
de movimiento vectoriales, lo que significa que existe un vector
que depende del tiempo según la ecuación.
que es equivalente a
Las componentes de  son tres momentos, tres coordenadas y el
tiempo.
Este es un sistema de ecuaciones con seis variables y el tiempo.
Además, aquí las derivadas son parciales porque se tienen
seis variables y el tiempo en cada ecuación; el hecho es que
tenemos el mismo problema repetido seis veces; ahora bien, si se
evita la derivación en todo su detalle, pueden considerarse las
cosas de tal modo que las ecuaciones salgan exactamente iguales,
tomando en cuenta que las
son tres momentos, tres coordenadas y el
tiempo.
Este es un sistema de ecuaciones con seis variables y el tiempo.
Además, aquí las derivadas son parciales porque se tienen
seis variables y el tiempo en cada ecuación; el hecho es que
tenemos el mismo problema repetido seis veces; ahora bien, si se
evita la derivación en todo su detalle, pueden considerarse las
cosas de tal modo que las ecuaciones salgan exactamente iguales,
tomando en cuenta que las  son vectores, las
son vectores, las  son vectores.
Se tiene un argumento vectorial
son vectores.
Se tiene un argumento vectorial  ;
; 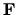 indica que existen
seis funciones que dependen de seis variables. Si se considera que los
seis argumentos son vectores y que la función es un vector, es
entonces correcto pensar que las fórmulas para una variable expuestas
en hojas anteriores tiene también validez aquí. Teniendo en
cuenta la naturaleza vectorial de nuestra función, podemos ahora
traducirla convenientemente.
Otra cosa que puede verse, aunque no influye, es que en este
problema, la funcion hamiltoniana no depende del tiempo. Nuestras
ecuaciones, por consiguiente, sólo son dependientes de las
indica que existen
seis funciones que dependen de seis variables. Si se considera que los
seis argumentos son vectores y que la función es un vector, es
entonces correcto pensar que las fórmulas para una variable expuestas
en hojas anteriores tiene también validez aquí. Teniendo en
cuenta la naturaleza vectorial de nuestra función, podemos ahora
traducirla convenientemente.
Otra cosa que puede verse, aunque no influye, es que en este
problema, la funcion hamiltoniana no depende del tiempo. Nuestras
ecuaciones, por consiguiente, sólo son dependientes de las  , por
lo que no se escribirá explicitamente al tiempo como argumento.
La discusión de los métodos que hemos presentado es solamente
descriptiva. Para una presentación rigurosa puede consultarse
cualquier libro de Análisis Numérico, por ejemplo, el de Kunz [10]
y Hildebrand [11].
, por
lo que no se escribirá explicitamente al tiempo como argumento.
La discusión de los métodos que hemos presentado es solamente
descriptiva. Para una presentación rigurosa puede consultarse
cualquier libro de Análisis Numérico, por ejemplo, el de Kunz [10]
y Hildebrand [11].




Next: Descripción del programa
Previous: Generalidades sobre el monopolo
Contents
Pedro Hernandez
2006-02-20
![]() , si se toma
, si se toma ![]() en
en ![]() , al desarrollar la función en serie de potencias alrededor de
, al desarrollar la función en serie de potencias alrededor de
![]() se tiene:
se tiene:
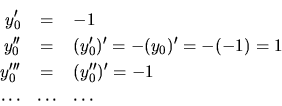
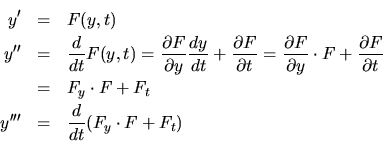
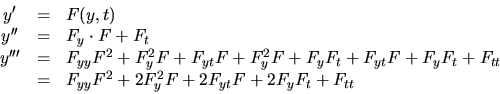

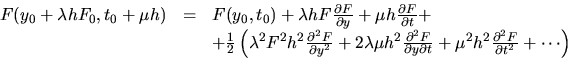
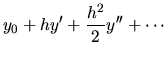
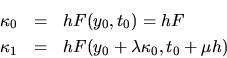
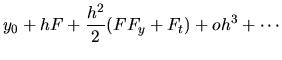
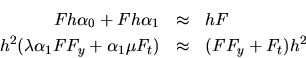
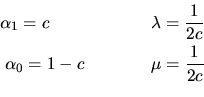
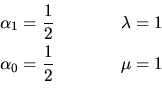
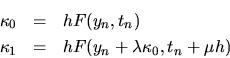

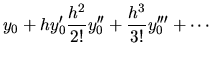
![]() . En ese caso se tiene
. En ese caso se tiene