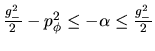Next: Energías negativas
Up: Algunos ejemplos de configuraciones
Previous: Algunos ejemplos de configuraciones
Contents
Partículas Atrapadas (Energías Positivas)
Deseamos saber si es posible que existan estados ligados con
energías positivas en el caso del dipolo magnético. Para
eso encontramos que hay dos configuraciones posibles de las curvas
que dependen de  ; lo que debe tenerse en ambos casos es que
la recta para energía nula deber estar comprendida entre la
asíntota horizontal tangente al mínimo de la curva. Una
configuración es la siguiente:
; lo que debe tenerse en ambos casos es que
la recta para energía nula deber estar comprendida entre la
asíntota horizontal tangente al mínimo de la curva. Una
configuración es la siguiente:
Figure 4.1:
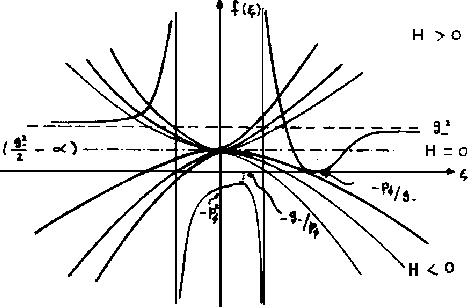 |
Para esta configuración debe cumplirse que
Esta es la condición para que el cero de la función esté
localizado en algún valor 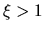 .
La recta que define el cero de la energía debe satisfacer la
condición
.
La recta que define el cero de la energía debe satisfacer la
condición
Para la variable  cualquier solución con sentido físico
debe cumplir con la condición de que la recta que define el cero
de la energía intersecta la rama inferior de la otra curva.
Entonces, siempre se debe exigir que se cumpla la desigualdad:
cualquier solución con sentido físico
debe cumplir con la condición de que la recta que define el cero
de la energía intersecta la rama inferior de la otra curva.
Entonces, siempre se debe exigir que se cumpla la desigualdad:
Para el dipolo magnético 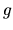 vale cero, entonces
vale cero, entonces
Las condiciones para  y para
y para  deberán cumplirse
simultáneamente. Es decir, que para la configuración de las curvas
de que estamos considerando debemos tener:
deberán cumplirse
simultáneamente. Es decir, que para la configuración de las curvas
de que estamos considerando debemos tener:
Con (1), (2) y (3) podemos formar otra desigualdad:
(4) resulta ser una contradicción, de donde concluimos que para
la configuración que hemos elegido no puede haber
partículas atrapadas.
Nos queda todavía ver la otra configuración, la cual consiste
en que el cero de la función está en el intervalo 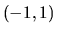 y que el
mínimo esta situado del lado derecho. La configuración de las
curvas se ilustra en la siguiente figura
y que el
mínimo esta situado del lado derecho. La configuración de las
curvas se ilustra en la siguiente figura
Figure 4.2:
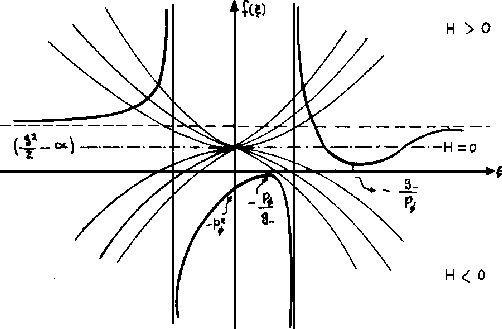 |
El valor de la función en el punto
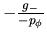 es
es
Entonces, para 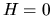 , deberá cumplirse la desigualdad
, deberá cumplirse la desigualdad
por lo tanto
Además, debe cumplirse que
Por lo tanto se tienen tres condiciones para la configuración
que hemos tomado:
-
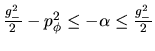
-
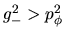
-
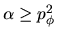 ó
ó
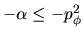
Podemos formar la desigualdad
Nuevamente hemos llegado a una contradicción por lo que concluimos
que en ningún caso la separación de las variables nos lleva a
partículas atrapadas con energía positiva. Debemos recordar
que la separación se consiguió sumando un potencial repulsivo a la
hamiltoniana. Podemos decir que por lo menos, la adición de un
potencial de ese estilo conduce a que no haya el tipo de trayectorias
como las que hemos buscado.




Next: Energías negativas
Up: Algunos ejemplos de configuraciones
Previous: Algunos ejemplos de configuraciones
Contents
Pedro Hernandez
2006-02-20

![\begin{displaymath}
\frac{(p_{\phi} + g_-\xi_{ext})^2}{\xi_{ext}^2 - 1} =
\fra...
...}{p_\phi}])^2}{\frac{g_-^2}{p_\phi^2}
-1} = g_-^2 - p_\phi^2
\end{displaymath}](img365.png)