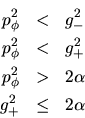Next: Estudio del movimiento considerando
Up: Algunos ejemplos de configuraciones
Previous: Dos cargas magnéticas
Contents
Para energías positivas no hemos encontrado partículas
atrapadas, veamos las condiciones que deben cumplirse para que
haya trayectorias ligadas (si las hay) con energías
negativas, escribiremos la forma que deben tener las ecuaciones
(3) de la página 15.
para las curvas de  hay dos posibilidades, dependiendo de si
hay dos posibilidades, dependiendo de si
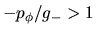 ó
ó
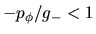 . Sabemos que
dicha cantidad corresponde al cero de la función y que su valor
determina si la curva toca al eje horizontal dentro del intervalo
. Sabemos que
dicha cantidad corresponde al cero de la función y que su valor
determina si la curva toca al eje horizontal dentro del intervalo
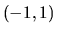 o fuera de él. El estudio del movimiento se hace de
la misma manera que se ha hecho anteriormente.
o fuera de él. El estudio del movimiento se hace de
la misma manera que se ha hecho anteriormente.
Caso 1.- consideramos primero para  la posibilidad
la posibilidad
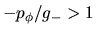 . Tendremos entonces
. Tendremos entonces
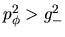 . Debe
pedirse como en casos anteriores, que la intersección de la
parábola con el eje vertical sea positiva o cero, es decir:
. Debe
pedirse como en casos anteriores, que la intersección de la
parábola con el eje vertical sea positiva o cero, es decir:
Las condiciones para  son del mismo tipo, hay dos
posibilidades:
son del mismo tipo, hay dos
posibilidades:
 y
y
 veremos enseguida la primera, es decir
veremos enseguida la primera, es decir
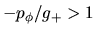 , que es
equivalente a
, que es
equivalente a
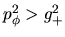 .
El valor de la función
.
El valor de la función 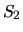 en el punto
en el punto 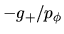 (valor
extremo) es
(valor
extremo) es
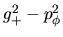 y ese valor debe ser menor o igual
a la intersección de la parábola con el eje vertical, es
decir:
y ese valor debe ser menor o igual
a la intersección de la parábola con el eje vertical, es
decir:
Así, tenemos que
Tenemos entonces:
En estas relaciones, tomando la segunda y la cuarta tendremos:
Es decir:
Esta es una contradicción con la primera y por lo tanto
descartamos el caso 1.
Caso 2.- Tomemos ahora la segunda posibilidad para  a saber:
a saber:
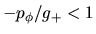 es decir
es decir
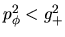 . Tomaremos
aquí para la variable
. Tomaremos
aquí para la variable  las mismas posibilidades que en
el caso anterior. La intersección de la parábola con el eje
vertical debe ser ahora negativa o cero:
las mismas posibilidades que en
el caso anterior. La intersección de la parábola con el eje
vertical debe ser ahora negativa o cero:
Resumiendo, se tiene
Llegamos a una contradicción y por lo tanto descartamos el caso 2.
Caso 3.- Combinaremos ahora la segunda posibilidad para  con la primera para
con la primera para  .
.
Para  se tiene:
se tiene:
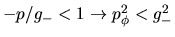 El valor de la función en el punto
El valor de la función en el punto
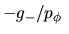 es
es
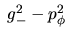 Debemos tener por consiguiente:
Debemos tener por consiguiente:
Eso porque
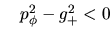 Las condiciones para
Las condiciones para  ya se encontraron en el caso 1, entonces
tendremos:
ya se encontraron en el caso 1, entonces
tendremos:
llegamos a una contradicción y tenemos descartado el caso 3.
Caso 4.- Nos queda el último caso que consiste en tomar la segunda
posibilidad para  con la segunda para
con la segunda para  . Hemos
encontrado en los casos 2 y 3 las condiciones que deben
cumplirse para las dos posibilidades mencionadas (en el 2 para
. Hemos
encontrado en los casos 2 y 3 las condiciones que deben
cumplirse para las dos posibilidades mencionadas (en el 2 para
 y en 3 para
y en 3 para  ); las relaciones que mencionamos son:
); las relaciones que mencionamos son:
combinando la segunda con la cuarta se tiene:
Esto está en conflicto con la tercera relación, entonces lo que
encontramos que también hay que descartar el cuarto caso.
Conclusión de todo lo anterior:
No se puede encontrar trayectorias ligadas cuando la carga en los dos
centros es puramente magnética.




Next: Estudio del movimiento considerando
Up: Algunos ejemplos de configuraciones
Previous: Dos cargas magnéticas
Contents
Pedro Hernandez
2006-02-20
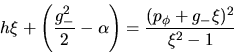
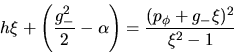
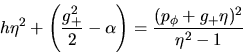
![]() la posibilidad
la posibilidad
![]() . Tendremos entonces
. Tendremos entonces
![]() . Debe
pedirse como en casos anteriores, que la intersección de la
parábola con el eje vertical sea positiva o cero, es decir:
. Debe
pedirse como en casos anteriores, que la intersección de la
parábola con el eje vertical sea positiva o cero, es decir:
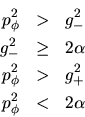
![]() a saber:
a saber:
![]() es decir
es decir
![]() . Tomaremos
aquí para la variable
. Tomaremos
aquí para la variable ![]() las mismas posibilidades que en
el caso anterior. La intersección de la parábola con el eje
vertical debe ser ahora negativa o cero:
las mismas posibilidades que en
el caso anterior. La intersección de la parábola con el eje
vertical debe ser ahora negativa o cero:
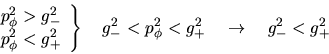
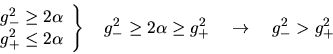
![]() con la primera para
con la primera para ![]() .
.
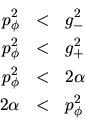
![]() con la segunda para
con la segunda para ![]() . Hemos
encontrado en los casos 2 y 3 las condiciones que deben
cumplirse para las dos posibilidades mencionadas (en el 2 para
. Hemos
encontrado en los casos 2 y 3 las condiciones que deben
cumplirse para las dos posibilidades mencionadas (en el 2 para
![]() y en 3 para
y en 3 para ![]() ); las relaciones que mencionamos son:
); las relaciones que mencionamos son: