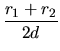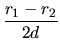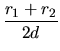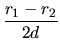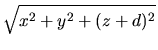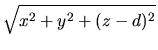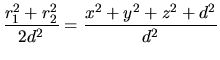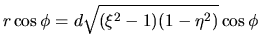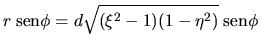Next: Ecuaciones de movimento
Up: Introducción
Previous: Introducción
Contents
En general, el propósito de nuestro trabajo consiste en determinar el
movimiento de una partícula en el campo de dos centros
coulombianos en los términos que hemos propuesto en páginas
anteriores. Los casos correspondientes a monopolos magnéticos,
problema de Kepler, dipolos, etc., son diferentes posibilidades
del problema. Entonces, las ecuaciones de movimiento se plantean
para dos centros y en cada caso se harán las consideraciones
necesarias. La naturaleza del problema nos sugiere utilizar
coordenadas elipsoidales y el método más adecuado para
realizar nuestro estudio es el uso de una formulación
hamiltoniana.
La definición de coordenadas elipsoidales es la siguiente: Se tienen dos
focos separados por una distancia de 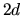 , en ellos vamos a colocar los centros
de fuerza mencionados. Las distancias de dichos centros a un punto
, en ellos vamos a colocar los centros
de fuerza mencionados. Las distancias de dichos centros a un punto 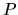 (donde
colocamos la carga de prueba) están representadas por
(donde
colocamos la carga de prueba) están representadas por 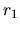 y
y 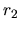 .
Las coordenadas se toman como:
.
Las coordenadas se toman como:
La línea de los centros se toma como eje 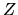 , alrededor de dicho eje
se considera un ángulo
, alrededor de dicho eje
se considera un ángulo 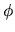 como tercera coordenada. La interpretación de
dichas coordenadas es la siguiente. Los valores constantes de
como tercera coordenada. La interpretación de
dichas coordenadas es la siguiente. Los valores constantes de  definen
elipses cuyos focos son precisamente los dos centros y los valores de
definen
elipses cuyos focos son precisamente los dos centros y los valores de  deteminan hipérbolas con los mismos focos. En tres dimensiones se tendrán
figuras de revolución alrededor del eje
deteminan hipérbolas con los mismos focos. En tres dimensiones se tendrán
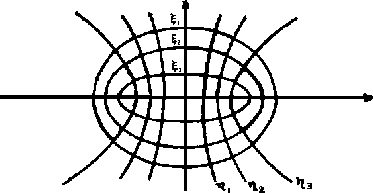
figuras de revolución alrededor del eje 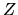 . En seguida mostramos el caso
bidimensional.
. En seguida mostramos el caso
bidimensional.
Figure 1.1:
coordenadas elípticas
 |
Además, se ve fácilmente que
Se tienen algunas relaciones que nos serán útiles:
Estas relaciones permiten en cualquier momento escribir en coordenadas
elipsoidales cantidades expresadas en coordenadas cartesianas.




Next: Ecuaciones de movimento
Up: Introducción
Previous: Introducción
Contents
Pedro Hernandez
2006-02-20