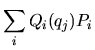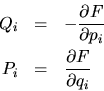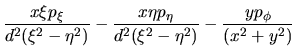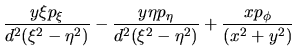Next: Interacción con el campo
Up: Introducción
Previous: Planteamiento del problema
Contents
Una vez planteada la naturaleza del problema el siguiente paso
consiste en establecer las ecuaciones de movimiento en forma hamiltoniana,
primero vamos a ver como se escribe la energía cinética en términos de las
nuevas coordenadas. Recordemos que en coordenadas cartesianas y en ausencia
de potencial vectorial la energía cinética está dada como:
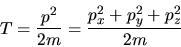 |
(I-2-1) |
Si deseamos expresar nuestras ecuaciones en coordenadas elipsoidales
conviene formar una función generadora de transformaciones
canónicas del tipo 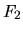 [1] de la manera siguiente:
[1] de la manera siguiente:
donde las 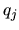 son las viejas coordenadas y las
son las viejas coordenadas y las 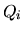 y las
y las 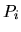 son
las nuevas coordenadas y los nuevos momentos respectivamente. Ya sabemos
de la teoría que
son
las nuevas coordenadas y los nuevos momentos respectivamente. Ya sabemos
de la teoría que
con estas relaciones podemos encontrar los viejos momentos y
coordenadas en función de los nuevos.
En nuestro caso y de acuerdo con (I-2-2) se tiene:
y
Para 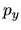 y
y  se obtienen relaciones semejantes. Una vez efectuadas
las operaciones, los resultados son:
se obtienen relaciones semejantes. Una vez efectuadas
las operaciones, los resultados son:
Teniendo ahora los viejos momentos se substituye en la expresión para la
energía cinética resultando lo siguiente:
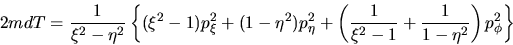 |
(I-2-4) |
con lo cual tenemos la energía cinética expresada
en coordenadas elipsoidales como era nuestro deseo. Una vez hecho
lo anterior debemos observar ciertas propiedades: Nótese que
cuando el valor de  se acerca a la unidad, las elipses van
siendo cada vez más cerradas hasta llegar al límite en que
se tiene una elipse degenerada en el segmento rectilíneo que
une los dos centros. También al llegar a la unidad del valor de
se acerca a la unidad, las elipses van
siendo cada vez más cerradas hasta llegar al límite en que
se tiene una elipse degenerada en el segmento rectilíneo que
une los dos centros. También al llegar a la unidad del valor de
 las hipérbolas se cierran hasta que se llega a una
hipérbola degenerada que corresponde a la parte comprendida
fuera del segmento que une los centros.
Cuando una de las dos variables vale uno, la otra puede tomar cualquier
valor diferente de la unidad, en esos casos no hay singularidades,
pero sí cuando las dos variables toman el mencionado valor y
que es equivalente a estar colocado en uno de los dos centros,
como puede verse de (I-1-1) ya que
las hipérbolas se cierran hasta que se llega a una
hipérbola degenerada que corresponde a la parte comprendida
fuera del segmento que une los centros.
Cuando una de las dos variables vale uno, la otra puede tomar cualquier
valor diferente de la unidad, en esos casos no hay singularidades,
pero sí cuando las dos variables toman el mencionado valor y
que es equivalente a estar colocado en uno de los dos centros,
como puede verse de (I-1-1) ya que 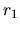 y
y 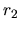 no pueden
anularse simultáneamente. También puede verse en (I-2-4) que
la energía cinética va a ser distorsionada por el factor
no pueden
anularse simultáneamente. También puede verse en (I-2-4) que
la energía cinética va a ser distorsionada por el factor
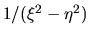 y que corresponde al recíproco del
producto
y que corresponde al recíproco del
producto 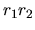 . Cuando dicho producto es muy pequeño su
recíproco es muy grande lo cual significa estar en la
vecindad de uno de los dos centros. Se observa también que
cuando
. Cuando dicho producto es muy pequeño su
recíproco es muy grande lo cual significa estar en la
vecindad de uno de los dos centros. Se observa también que
cuando
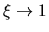 el factor que multiplica a
el factor que multiplica a 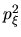 es muy pequeño lo que va a ser compensado con el crecimiento de
es muy pequeño lo que va a ser compensado con el crecimiento de
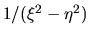 de tal modo que el producto de los dos se
mantiene fijo y lo mismo se tiene con la parte correspondiente a
la variable
de tal modo que el producto de los dos se
mantiene fijo y lo mismo se tiene con la parte correspondiente a
la variable  . Entonces, esos dos momentos pueden tomar
valores muy grandes, pero debe señalarse que dichos momentos no
son únicamente de la forma
. Entonces, esos dos momentos pueden tomar
valores muy grandes, pero debe señalarse que dichos momentos no
son únicamente de la forma 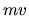 sino que hay un factor de peso
que toma en cuenta el cambio de coordenadas rectangulares a
curvilíneas provocando que aparezcan distorsiones en la
vecindad de los puntos ya mencionados. Por lo que respecta al
coeficiente del momento
sino que hay un factor de peso
que toma en cuenta el cambio de coordenadas rectangulares a
curvilíneas provocando que aparezcan distorsiones en la
vecindad de los puntos ya mencionados. Por lo que respecta al
coeficiente del momento  este tienen singularidades en
torno al eje
este tienen singularidades en
torno al eje 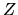 .
Hay que señalar que a excepción del factor
.
Hay que señalar que a excepción del factor
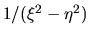 en la
energía cinética se tiene una suma de funciones con variables
separadas, por lo menos cuando tenemos a
en la
energía cinética se tiene una suma de funciones con variables
separadas, por lo menos cuando tenemos a  como constante. En
ese caso se tendrá la suma de una función sólo de
como constante. En
ese caso se tendrá la suma de una función sólo de  y una sólo de
y una sólo de
 . Puede decirse entonces que la energía cinética en este tipo
de coordenadas está casi separada; se verá que es separable en un
sentido que es útil.
Que la hamiltoniana sea o no separable va a depender de si lo es la
energía potencial, que es de la forma
. Puede decirse entonces que la energía cinética en este tipo
de coordenadas está casi separada; se verá que es separable en un
sentido que es útil.
Que la hamiltoniana sea o no separable va a depender de si lo es la
energía potencial, que es de la forma
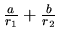 que
equivale a
que
equivale a
y se verá que al menos para potencial coulombiano se puede separar.
También hay separación cuando existe potencial vectorial debido a una
carga magnética como veremos más adelante. El sistema de coordenadas
empleado es uno de los pocos en que el problema es separable (en
coordenadas cartesianas esto no es posible).




Next: Interacción con el campo
Up: Introducción
Previous: Planteamiento del problema
Contents
Pedro Hernandez
2006-02-20