


Next: Algebra regular
Up: Jerarquía de Chomsky
Previous: Tipo 2 o libres de contexto
Contents
Las producciones de este tipo de gramáticas son de la forma
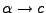 , donde
, donde
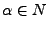 y
y 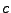 cumple con que,
cumple con que, 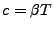 donde
donde
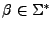 y
y 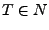 . Sólo tienen un no terminal
. Sólo tienen un no terminal 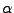 en el lado izquierdo
de la producción, el lado derecho de la producción debe contener una cadena formada de símbolos terminales y no terminales teniendo como máximo un no terminal que debe estar al extremo derecho de la cadena.
Opcionalmente se puede invertir la definición diciendo que se debe contener un no terminal al extremo izquierdo de cada producción, esta variación en la definición invierte el lenguaje generado por la gramática.
en el lado izquierdo
de la producción, el lado derecho de la producción debe contener una cadena formada de símbolos terminales y no terminales teniendo como máximo un no terminal que debe estar al extremo derecho de la cadena.
Opcionalmente se puede invertir la definición diciendo que se debe contener un no terminal al extremo izquierdo de cada producción, esta variación en la definición invierte el lenguaje generado por la gramática.
A las gramáticas que tiene el no terminal en el extremo derecho de la producción se les llama lineales por la derecha, las que lo tienen en el extremo derecho se les llama lineales por la izquierda.
El lenguaje producido por este tipo de gramáticas puede ser reconocido por un autómata finito como el mencionado en la sección 2.5.
Nota:
Un aspecto esencial de la jerarquía de Chomsky es que las gramáticas de nivel 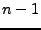 contienen a las de nivel
contienen a las de nivel 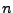 , es decir, las gramáticas no restringidas contienen a las gramáticas sensibles de contexto, que a su vez contienen a las gramáticas libres de contexto, que a su vez contienen a las gramáticas regulares.
, es decir, las gramáticas no restringidas contienen a las gramáticas sensibles de contexto, que a su vez contienen a las gramáticas libres de contexto, que a su vez contienen a las gramáticas regulares.
Dicho lo anterior, los lenguajes generados por gramáticas del nivel 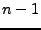 contienen a los lenguajes generados por gramáticas de nivel
contienen a los lenguajes generados por gramáticas de nivel 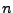 y, si un autómata acepta el lenguaje generado por una gramática de nivel
y, si un autómata acepta el lenguaje generado por una gramática de nivel 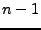 , entonces aceptará el lenguaje generado por la gramática de nivel
, entonces aceptará el lenguaje generado por la gramática de nivel 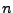 .
.



Next: Algebra regular
Up: Jerarquía de Chomsky
Previous: Tipo 2 o libres de contexto
Contents
Pablo Gerardo Padilla Beltran
2005-10-21
![]() contienen a las de nivel
contienen a las de nivel ![]() , es decir, las gramáticas no restringidas contienen a las gramáticas sensibles de contexto, que a su vez contienen a las gramáticas libres de contexto, que a su vez contienen a las gramáticas regulares.
, es decir, las gramáticas no restringidas contienen a las gramáticas sensibles de contexto, que a su vez contienen a las gramáticas libres de contexto, que a su vez contienen a las gramáticas regulares.
![]() contienen a los lenguajes generados por gramáticas de nivel
contienen a los lenguajes generados por gramáticas de nivel ![]() y, si un autómata acepta el lenguaje generado por una gramática de nivel
y, si un autómata acepta el lenguaje generado por una gramática de nivel ![]() , entonces aceptará el lenguaje generado por la gramática de nivel
, entonces aceptará el lenguaje generado por la gramática de nivel ![]() .
.