Teoría de los experimentos de Moore

Comenzaremos esta sección introduciendo la definición formal de una máquina de estado finitos o autómata finito. De acuerdo con Moore, una máquina de estados finitos o autómata finito es una 6-tupla 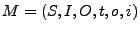$M=(S,I,O,t,o,i)$, donde:

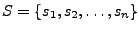• $S=\{s_1,s_2,\ldots,s_n\}$, es un conjunto finito de estados, para denotar que son los estados la máquina 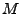$M$ se utilizará $S(M)$.
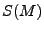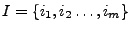• $I=\{i_1,i_2\ldots,i_m\}$, un conjunto finito de entradas que serán analizadas por alguna máquina 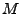$M$, para denotar que éstas entradas corresponden 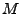$M$ se usará la notación $I(M)$.

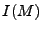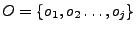• $O=\{o_1,o_2\ldots,o_j\}$, es un conjunto finito de palabras que son resultados o salidas que entregara algúna máquina, para denotar que estas salidas corresponden a la máquina 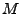$M$ se usará la notación $S(M)$.
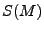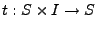• $t:S\times I\rightarrow S$, es una función de transición de estados como la explicada en la sección 2.5.

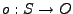• $o:S\rightarrow O$, es llamada la función de salida. Una máquina en estado 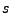$s$, esatara arrojando una salida 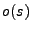$o(s)$ hasta que reciva una entrada 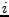$i$, entonces pasará al estado 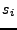$s_i$ y comenzará a emitir la salida $o(s_i)$.

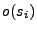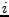• $i$, un estado especial, llamado estado inicial de la máquina.

Para dar una mejor idea de como imaginarse esto, hay que pensar que en algún momento, hay una máquina que se encuentra en el estado 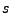$s$, y emitiendo una salida 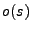$o(s)$. Esta máquina permanecerá en este estado, hasta que reciba una entrada 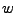$w$, entoncés cambiará su estado inmediatamente a 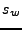$s_w$, y comenzará a emitir una salida 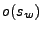$o(s_w)$. Inicialmente la máquina se encuentra en el estado 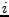$i$. Por comodidad se abrevia 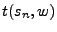$t(s_n,w)$ como $s_ {nw}$.
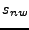Al igual que como hicímos con los autómatas finitos, es posible, y más comodo describir el comportamiento de una máquina por medio de una tabla, especificando las trancisiones de estado y dando los valores a 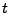$t$, para cada 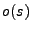$o(s)$, o con un diagrama de estados. 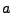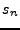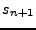En el último caso tendremos un nodo para cada estado, indicando su nombre y la salida que provoca, y una linea dirigida, marcada con $a$ que conecta el nodo $s_n$ con $s_{n+1}$, siempre que 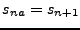$s_{na}=s_{n+1}$. El estado inicial esta marcado con una flecha entrante ( 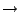$\rightarrow$). Para el caso particular de una máquina binaria, es decir, con sólo dos salidas diferentes, se puede indicar las salidas en 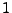$1$ con una flecha saliente( $\rightarrow$), tal como se muestra en la figura 2.

Figura 2: Diagrama de una máquina de tres estados, con dos salidas (0,1).

La tabla 2 corresponde a las transiciones de la máquina presentada en la figura 2, como se puede observar, es muy parecida a la tabla que describe a un AF, con la única diferencia que esta máquina arroja una salida dependiendo de su estado, en este caso sólo puede ser 0 ó 1, dado que es una máquina binaria.

Tabla 2: Tabla de transiciones de estado parar la máquina de la figura 2.

$t$	$a$	$b$	$o$
$s_n$	$s_{n+2}$	$s_{n+1}$	0
$s_{n+1}$	$s_{n+1}$	$s_n$	0
$s_{n+2}$	$s_{n+1}$	$s_{n+1}$	$1$

En la teoría de Moore, se considera que en cada experimento, la persona que experimenta con la máquina, no puede saber el estado de la máquina por otro medio que no sea su salida.
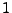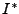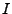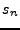Ajustaremos un poco las definiciones de la seccion 2.1, de tal manera que ahora una palabra será una secuencia finita de entradas. La longitud de la palabra, es la logitud de dicha secuencia, y la palabra vacía $1$, es la palabra de longitud 0. $I^*$ es el conjunto de todas la palabras de entrada en $I$. Si $s_n$ es un estado y 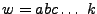$w=abc\ldots~k$ una palabra, entoncés, 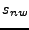$s_ {nw}$ denota el estado alcanzado desde 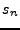$s_n$, al aplicar la secuencia $abc\ldots~k$ en orden. 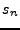Si la entrada de una máquina en algún estado $s_n$ es la cadena vacía, la máquina no cambia de estado, 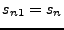$s_{n1}=s_n$. Un estado 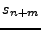$s_{n+m}$ es accesible desde otro estado 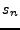$s_{n}$, sólo si, exite una palabra 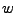$w$, de tal manera que 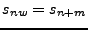$s_{nw}=s_{n+m}$, y es accesible si éste es accesible desde 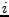$i$, el estado inicial.
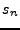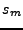También llamaremos a dos estados $s_n$ y $s_{m}$ indistinguibles, si se cumple que 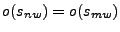$o(s_{nw})=o(s_{mw})$ para toda palabra 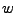$w$. Esta definición será útil aún si se trata de dos máuqinas diferentes, ya que sólo se necesita que dichas máquinas tengan el mismo conjunto de entradas 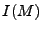$I(M)$ y salidas 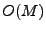$O(M)$. Más adelante se verá que, a veces, es posible que una máquina reemplace a otra, sólo si, éstas dos se comportan de la misma manera, bajo las mismas entradas. Esto puede ser bueno si la nueva máquina es menos compleja.

La mayor parte de la notación de esta sección es tomada de [JC71], así que 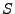$S$ viene de la palabra en íngles state, al igual que las demás letras utilizadas.