


Next: Teoría de eventos regulares
Up: Teoría de los experimentos
Previous: Teoría de los experimentos
Contents
En la teoría de los experimentos de Moore, un experimento se define como una función
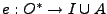 , donde
, donde 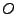 es el conjunto de todo los resultados que puede entregar la máquina,
es el conjunto de todo los resultados que puede entregar la máquina, 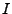 es son las entradas y
es son las entradas y  es un conjunto de respuestas donde
es un conjunto de respuestas donde
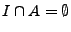 .
.
Para aplicar la función 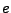 sobre alguna máquina
sobre alguna máquina 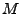 , es necesario poner a la máquina a analizar una cadena
, es necesario poner a la máquina a analizar una cadena
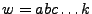 , después de analizarla, la máquina nos proporcionará una palabra, resultado de aplicar la función
, después de analizarla, la máquina nos proporcionará una palabra, resultado de aplicar la función 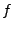 que analiza la cadena
que analiza la cadena 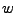 , partiendo de un estado
, partiendo de un estado 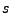 .
A esta palabra resultante se le aplica la función
.
A esta palabra resultante se le aplica la función 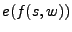 , si el resultado
, si el resultado 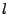 esta en
esta en 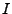 , se concatena
, se concatena 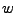 con
con 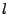 y se vuelve a procesar ahora la cadena
y se vuelve a procesar ahora la cadena 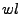 en la máquina con
en la máquina con 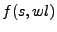 , en caso de que
, en caso de que 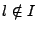 , indica que
, indica que
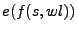 es una respuesta, llamada salida de
es una respuesta, llamada salida de 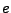 en
en 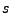 .
.
El objetivo de realizar estos experimentos es saber si podemos distinguir entre dos estados de una máquina analizando unicamente la salida, para esto se experimenta con dicha máquina de tal manera de que se pueda distinguir un estado de otro sólo analizando la longitud de la palabra resultante del experimento.
Se definen diferentes tipos de máquinas dependiendo de las restricciones para el número de estados, entradas y salidas, pero la forma de distinguir estados de diferentes máquinas es similar, se analiza la longitud de la palabra resultante de los experimentos realizados sobre las diferentes máquinas. Incluso se puede determinar con un experimento, si una máquina pertenece o a un conjunto
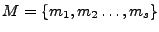 de máquinas, para esto es necesario que los estados de todas y cada una de las máquinas puedan ser distinguidos.
de máquinas, para esto es necesario que los estados de todas y cada una de las máquinas puedan ser distinguidos.
Como ya mencione la teoría de los experimentos de Moore, se centra en la capacidad de distinguir en entre estados que pueden ser de una misma máquina o de distintas máquinas, ésto nos da la posibilidad de decir que si las salida o resultados de dos máquinas son indistiguibles para toda salida, entonces las dos máquinas realizan el mismo análisis, ésto no implíca que la complejidad de las dos sea la misma.
Si se pueden obtener de dos máquinas diferentes se pueden obtener los mismos resultados y cada uno de los estados de estas máquinas son indistinguibles, entonces se dice que hay isomorfismo entre éllas y tendrán el mismo comportamiento. Sean 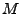 y
y 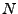 dos máquinas y
dos máquinas y 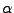 y
y 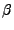 los conjuntos estados de
los conjuntos estados de 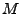 y
y 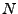 respectivamente y para toda cadena o entrada
respectivamente y para toda cadena o entrada 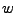 que se le aplique a la máquina, la función de salida
que se le aplique a la máquina, la función de salida
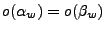 , tenemos dos máquinas con el mismo comportamiento y por lo tanto isomórficas.
, tenemos dos máquinas con el mismo comportamiento y por lo tanto isomórficas.
Ahora podemos decir que es posible que algunos autómatas de los mencionados en la sección 2.6.2, pueden comportarse igual que algún autómata de otro tipo, y ésto concuerda con la jerarquía de Chomsky. Por lo tanto, aunque una máquina de mayor complejidad pueda realizar algún analizis, bien podría utilizarse una máquina más simple sin perdida de eficiencia.



Next: Teoría de eventos regulares
Up: Teoría de los experimentos
Previous: Teoría de los experimentos
Contents
Pablo Gerardo Padilla Beltran
2005-10-21