


Next: Definiciones
Up: Algebra regular
Previous: Experimentos
Contents
Teoría de eventos regulares de Kleene y expresiones
En esta sección podremos veremos como es posible representar el comportamiento de un autómata finito por medio de una matriz de transición de estados cuyas entradas son expresiones regulares que definen un lenguaje cada una. A partir de la matriz de transición, podemos conocer que lenguaje aceptará algún autómata dependiendo de su estado inicial y su estado o estados finales, de hecho nosotros podemos indicar cual queremos que sea su estado inicial y su estado o estados finales y así especificar el lenguaje que aceptará dicho autómata. Antes de entrar en detalles, veremos una introducción a la teoría de eventos regulares definida por Stephen Cole Kleene.
Tomemos una máquina 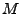 con estado inicial
con estado inicial 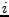 . En la teoría de eventos regulares de Kleene se define
. En la teoría de eventos regulares de Kleene se define
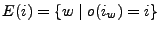 , como el conjunto de todas las cadenas que lleven a una máquina
, como el conjunto de todas las cadenas que lleven a una máquina 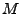 de su estado inicial
de su estado inicial 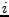 , a estados en los cuales la salida de la misma sea
, a estados en los cuales la salida de la misma sea 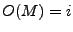 . De esta manera el comportamiento de dicha máquina esta caracterizado por los conjuntos
. De esta manera el comportamiento de dicha máquina esta caracterizado por los conjuntos
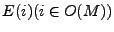 . Se dice que un conjunto
. Se dice que un conjunto 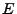 es representable si, existe una máquina
es representable si, existe una máquina 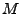 y una salida
y una salida 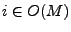 de tal manera que
de tal manera que 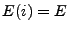 , es decir,
, es decir, 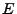 esta formado por todas las cadenas que cumplen con la definición de
esta formado por todas las cadenas que cumplen con la definición de 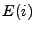 .
.
Subsections



Next: Definiciones
Up: Algebra regular
Previous: Experimentos
Contents
Pablo Gerardo Padilla Beltran
2005-10-21
![]() con estado inicial
con estado inicial ![]() . En la teoría de eventos regulares de Kleene se define
. En la teoría de eventos regulares de Kleene se define
![]() , como el conjunto de todas las cadenas que lleven a una máquina
, como el conjunto de todas las cadenas que lleven a una máquina ![]() de su estado inicial
de su estado inicial ![]() , a estados en los cuales la salida de la misma sea
, a estados en los cuales la salida de la misma sea ![]() . De esta manera el comportamiento de dicha máquina esta caracterizado por los conjuntos
. De esta manera el comportamiento de dicha máquina esta caracterizado por los conjuntos
![]() . Se dice que un conjunto
. Se dice que un conjunto ![]() es representable si, existe una máquina
es representable si, existe una máquina ![]() y una salida
y una salida ![]() de tal manera que
de tal manera que ![]() , es decir,
, es decir, ![]() esta formado por todas las cadenas que cumplen con la definición de
esta formado por todas las cadenas que cumplen con la definición de ![]() .
.