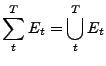


Next: Operaciones regulares
Up: Teoría de eventos regulares
Previous: Teoría de eventos regulares
Contents
Se ha mencionado que una cadena es una secuencia, posiblemente vacía de símbolos o entradas, ahora definiremos un evento como un conjunto arbitrario de cadenas. No podemos distinguir algún símbolo de la palabra de longitud 1 correspondiente a dicho símbolo, tampoco podemos distinguir alguna palabra y el correspondiente evento de cardinalidad 1, pero podemos distinguir entre el evento vacío que no contiene palabras, y el evento unitario que contiene unicamente la cadena vacía
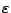 . Llamaremos a
. Llamaremos a 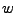 una ocurrencia del evento
una ocurrencia del evento 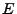 si,
si, 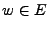 .
.
El objetivo de Kleene era describir la relación entre un organismo animal y su medio ambiente. El organismo puede detectar algún evento en su medio ambiente, unicamente observando algunas propiedades especiales de los estímulos que recibe. Para propósitos matemáticos, podemos identificar un evento a partir de las secuencias de entrada (estímulos), las cuales corresponden a la ocurrencia de algún evento.
Ahora definiremos las operaciones algebraicas básicas que se pueden realizar con eventos:
Ahora podemos definir la estrella de 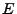 , como
, como
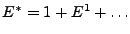 , que es la suma de las potencias de
, que es la suma de las potencias de 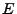 . Las potencias
. Las potencias 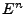 se definen inductivamente como,
se definen inductivamente como, 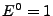 ,
,
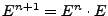 . La
. La 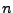 -ésima suma parcial de las potencias de
-ésima suma parcial de las potencias de 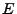 es
es
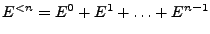 , también podemos usar
, también podemos usar
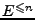 para denotar
para denotar
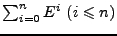 ,
,
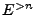 para
para
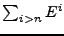
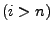 , etc.
, etc.



Next: Operaciones regulares
Up: Teoría de eventos regulares
Previous: Teoría de eventos regulares
Contents
Pablo Gerardo Padilla Beltran
2005-10-21